Trouver d'abord, chercher ensuite.
(Cocteau)

dont je n'ai pas de réponse ou pas de réponse claire :

• (R. Stanley.) On inscrit un rectangle dans un cercle, et un triangle isocèle dans une des lunules. Quelles doivent être les dimensions du rectangle pour qu'il ait la même aire que le triangle ?
• (R. Stanley.) On appelle S l'ensemble des matrices 10x10, dont les coefficients sont 0 ou 1, et dont la somme des coefficients est 84. Calculer le maximum des rayons spectraux des éléments de S.
• (V. Fock, Arnold.) Trouver une courbe fermée lisse (pas simple) dans le plan telle qu'il y ait plusieurs façons d'immerger un disque dans l'espace de sorte que le bord du disque soit la courbe.
• (géométrie) Y a-t-il une raison "simple" pour laquelle le groupe fondamental d'une surface orientable n'a pas d'élément d'ordre fini ?
• (physique) Pourquoi les sprinters doivent-ils être si musclés des épaules et des bras ? Faut-il lancer les bras en l'air quand on fait du saut en hauteur ?
• (mathématico-physique) Pourquoi mon compas trace-t-il des cercles ? Pourquoi semble-t-il y avoir une métrique privilégiée dans "l'espace sensible" ?
• (physique ; origine C. Mignard) Une corde sans masse pend à une poulie sans frottements. Deux singes de même masse s'y suspendent à la même hauteur. L'un des deux reste immobile, l'autre se met à grimper à vitesse constante (par rapport à la corde). Que se passe-t-il ?
• (polémique) La Didactique serait-elle née sans la réforme des "maths modernes" ?

• (Trigonométrie sphérique) Est-ce que le soleil se couche sur la terre ou sur la mer à Marseille ?
• (R. Stanley.)
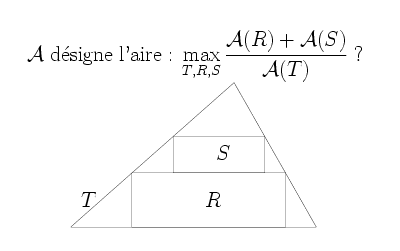
• (Question d'A. Tchoudjem, réponse d'A. Ould Houcine)
• (B. Lass) Etant donné un polygone convexe, un des disques circonscrits à un triangle formé de trois sommets consécutifs contient tous les sommets. Réponse de J.-B. Rouquier et correspondance Rouquier-Lass.
• (M. Polyak) Un tableau est attaché par une longue ficelle. Peut-on trouver un moyen de le fixer sur deux clous plantés dans un mur de sorte que si on en enlève un des deux, le tableau tombe ? Réponse.
• (M. Polyak) Tout entier multiple de 6 est somme de quatre cubes. Tout entier est somme de cinq cubes.
  (Indication : la dérivée seconde de n -> n³ est : n -> 6n.)
• (O. Mathieu) Développement décimal de 1/p et avatars.
  • Calculer sans machine les 110^ème, 111^ème, 112^ème et 113^ème décimales de 1/113.
  • Soit p un nombre premier impair. La (p-1)/2-ème décimale de 1/p ne dépend que de la classe de p modulo 40 et la (p-3)/2-ème décimale de 1/p ne dépend que de la classe de p modulo 200.
  • Si, de plus, p est différent de 3 et 7, la (p+1)/2-ème décimale de 1/p est 0 ou 9.
  • Montrer que dans le développement de 1/2003 en base 2, on trouve, en moyenne, autant de 1 que de 0.
• (J. Alev) On sait que le groupe des isométries qui préservent un icosaèdre régulier est le groupe alterné A₅ ; notons G son image réciproque par la projection classique SU(2) -> SO(3). Comment réaliser G plus simplement ?
• Comment décrire les cercles du demi-plan de Poincaré ? (Un cercle est l'ensemble des points équidistants d'un point donné pour la métrique de Poincaré.)
• (C. Bonnafé) Imaginons un bateau sur un lac. Sur ce bateau, il y a un bon gros caillou en bon granit bien dur. On le jette à l'eau sans rien éclabousser. Est-ce que l'eau du lac monte ou descend ?
• (classique) Pourquoi un miroir échange-t-il la gauche et la droite, mais pas le haut et le bas ?
• (no comment) On parle souvent de nombres premiers jumeaux (un couple de nombres premiers de la forme (p,p+2)). Or, (3,5,7) forment des nombres premiers triplés. En existe-t-il une infinité d'autres ? (Existe-t-il une infinité d'entiers p tels que p, p+2, et p+4 soient premiers ?)
• (classique) Peut-on paver, avec des dominos 2x1, un échiquier dont on retire deux coins opposés ?

Si ces questions vous intéressent, tout email est bienvenu : germoni(at)igd.univ-lyon1.fr.

Retour à la page de l'Institut Girard Desargues

()