Joint French-Czech mathematics meeting
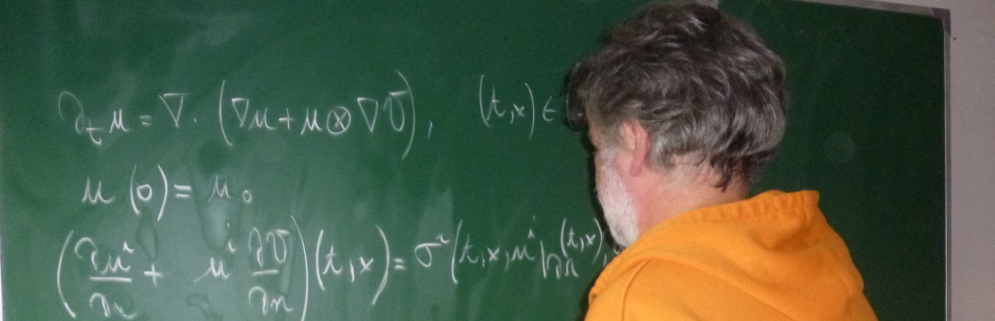
INSA-Lyon, November 29-30, 2018
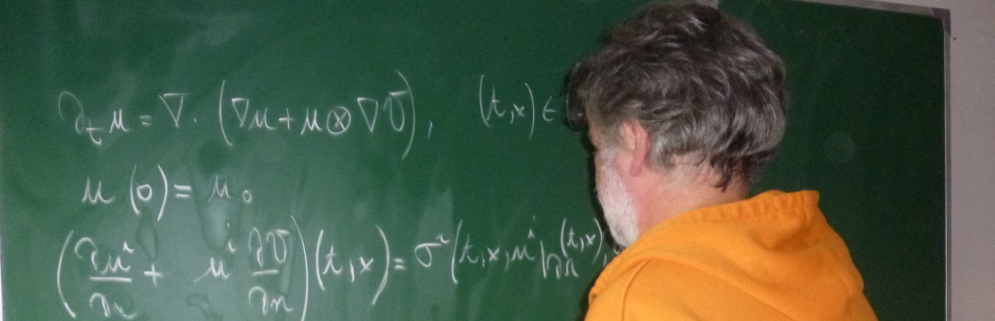
INSA-Lyon, November 29-30, 2018
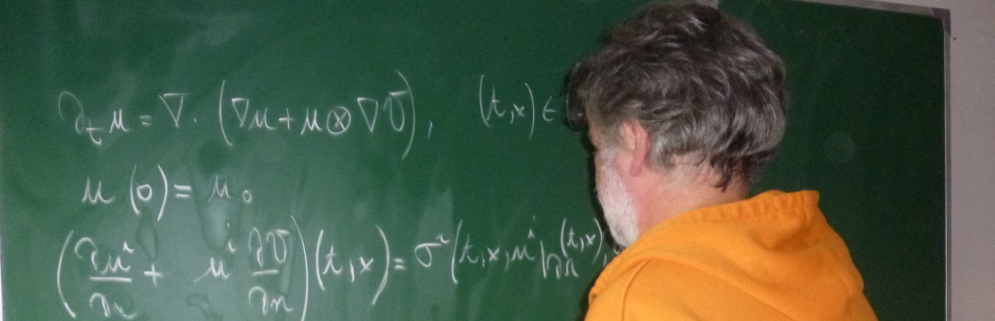
We shall investigate relations between renormalized solutions of the transport and continuity equations with transporting coefficient in Sobolev spaces and with possibly unbounded divergence. These considerations lead to several statements which are not covered by the DiPerna-Lions transport theory and its recent generaliazations by Bianchini, Bonicatto, as for example, almost uniqueness or almost compactness to the solutions to the pure transport equation. These conclusions have interesting applications in the mathematical theory of compressible fluids. We shall mention some of them.