Joint French-Czech mathematics meeting
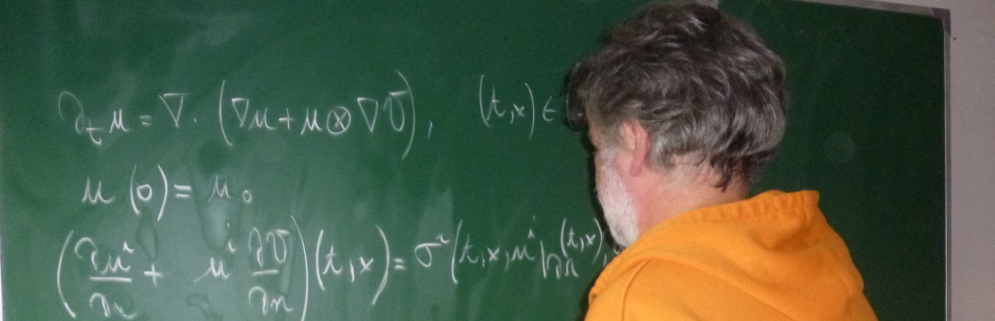
INSA-Lyon, November 29-30, 2018
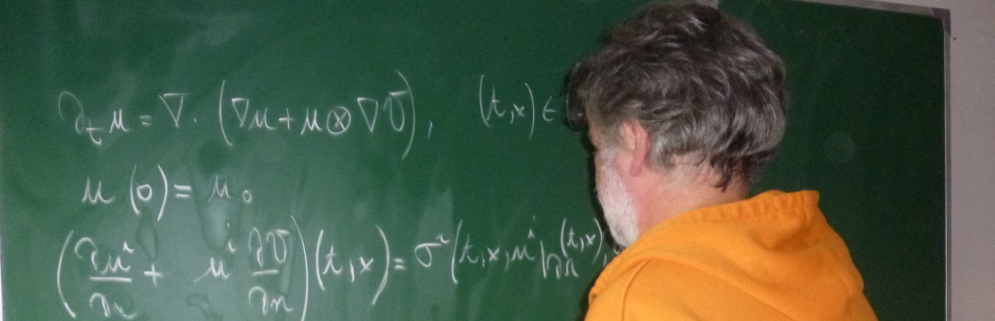
INSA-Lyon, November 29-30, 2018
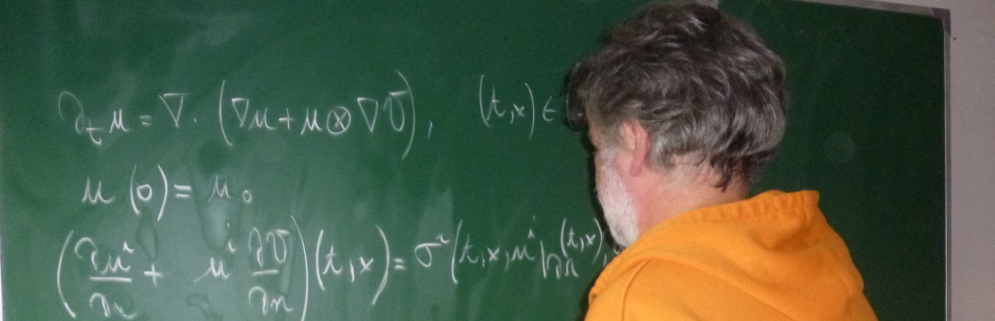
We analyze the stability of a dispersive medium immersed in vacuum (with Silver-Müller boundary condition in the exterior boundary) or vice versa. The dispersive medium model corresponds to the coupling between Maxwell's system and a first order ordinary differential equation (of parabolic type). For a dispersive medium coupled with vacuum, the ordinary differential equation will be set in a subset of the full domain. We show that this model is well-posed and is strongly stable in a closed subspace of the energy space. We further identify some sufficient conditions that guarantee the exponential or polynomial decay of the associated energy in this subspace.