INSA-Lyon, November 29-30, 2018
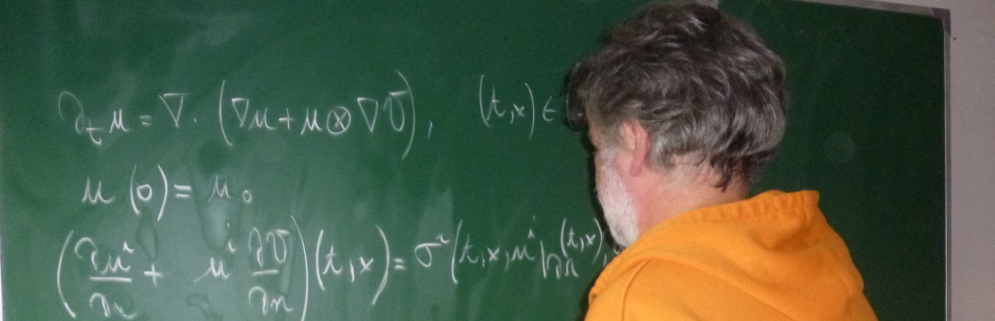
INSA-Lyon, November 29-30, 2018
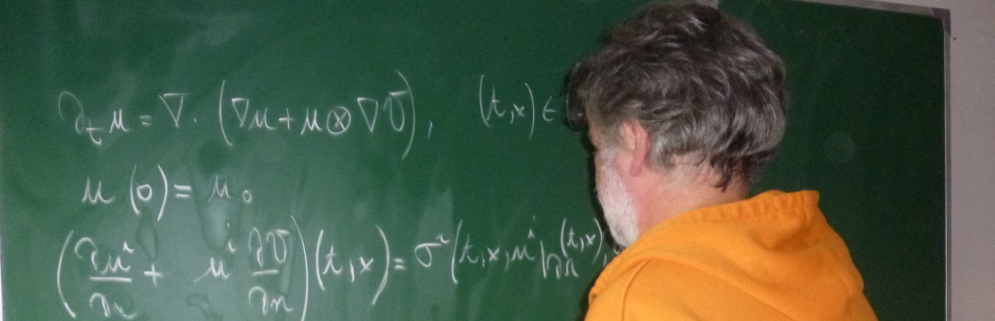
We propose thermodynamically consistent models for viscoelastic fluids with/without a stress diffusion term. In particular, we derive variants of compressible/incompressible Maxwell/Oldroyd-B/Giesekus models with/without a stress diffusion term in the evolution equation for the extra stress tensor. It is shown that the stress diffusion term can be interpreted either as a consequence of a nonlocal energy storage mechanism or as a consequence of a nonlocal entropy production mechanism. Different interpretations of the stress diffusion mechanism lead to different evolution equations for the temperature. The benefits of the knowledge of the thermodynamical background of the derived models are documented in the study of nonlinear stability of steady state solutions to the corresponding governing equations.