Joint French-Czech mathematics meeting
INSA-Lyon, November 29-30, 2018
INSA-Lyon, November 29-30, 2018
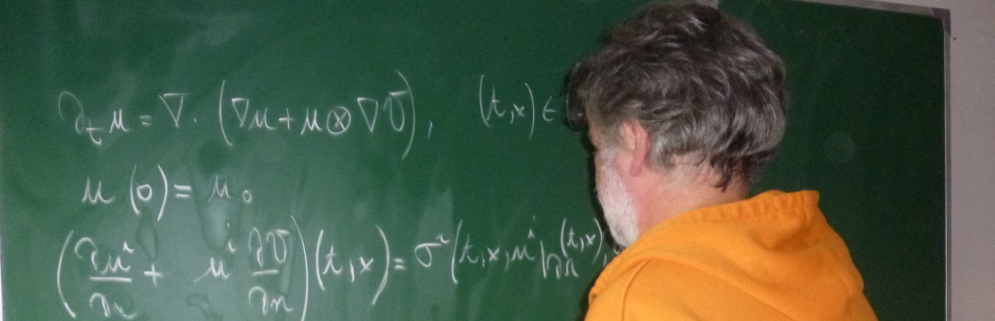
In the footstep of Gent & Lindley cavitation in rubber was viewed for a long time as a purely elastic phenomenon. In essence incipient point defects would expand into spherical cavities under deformations of the form x/|x|. Yet it had already been remarked early on, most notably by Williams & Schapery that doing so resulted in unrealistically high elastic strains along the boundary of the cavity. They had suggested that one should complement the Gent-Lindley picture by accounting for possible breakage of the crosslinks, hence introducing a modicum of fracture into the model. Actually the resulting picture, which does show a better fit with data, has to be amended because of the presence of a healing process for the crack. Here we report on the first attempt at introducing a dual fracture/healing mechanism in a rational description of fracture evolution and demonstrate the existence of a well posed quasi-static energetic evolution under the further topological restriction that the cracks be continua of finite length (compact connected). This is an existence result in the spirit of the original 2001 2d existence result for fracture evolution by G. Dal Maso & R. Toader for fracture only.
