Devoir maison - Modèle de Morris-Lecar MAJ 17/05

Q1 Lecture de l'article de Morris et Lecar 2 pts

Le modèle a été présenté dans un papier de 1981 par Catherine Morris et Harold Lecar.

C Morris, H Lecar, Voltage Oscillations in the Barnacle Giant Muscle Fiber, (1981) Biophys J 35:193-213.

Résumez en quelques mots cet article en indiquant :

• le modèle animal et le type d'expérience utilisé
• la ou les hypothèses que les auteurs ont voulu tester
• le type de modélisation utilisé
• les principaux résultats
• le message à retenir de cet article

(Note: Toutes les réponses se trouvent dans l'abstract de l'article.)

Q2 Fichiers EDO et solutions 5 pts

Initialisation des paramètres

I = 400;      % courant applique (muA/cm2)
duree = 200;  % duree de l'application du courant

g_L  =   2;   % conductance 'leak' (mS/cm2)
g_Ca =   4;   % conductance Ca++   (mS/cm2)
g_K  =   8;   % conductance K+     (mS/cm2)
V_L =  -50;   % potentiel d'equilibre correspondant au conductancs 'leak' (mV)
V_Ca = 100;   % potentiel d'equilibre correspondant au conductancs Ca++ (mV)
V_K =  -70;   % potentiel d'equilibre correspondant au conductancs K+ (mV)
V1 =  10.0;   % potentiel pour lequel M_ss = 0.5  (mV)
V2 =  15.0;   % inverse de la pente de la dependence de voltage de M_ss (mV)
V3 =  -1.0;   % potentiel pour lequel N_ss = 0.5  (mV)
V4 =  14.5;   % inverse de la pente de la dependence de voltage de W_ss (mV)
C  =    20;   % capacitance de la membranne (muF/cm2)
T0 =    15;   % Constante de temps pour ouverture des canaux (ms) (1/lambda dans le papier)

par = [I, duree, g_L, g_Ca, g_K, V_L, ...
        V_Ca, V_K, V1, V2, V3, V4, C, T0];

% paramètres de simulation
t0 = -20;
tfinal = 200;
tspan = [t0,tfinal];
options = odeset();

% Conditions initiales
IC = [  -35;
        0];

Créez un fichier Matlab script que vous appelerez simule_morrislecar.m.

Créez une fonction Matlab morrislecar qui implémente les équations de Morris-Lecar (équations 9 dans le papier).

Note (11/05): Comme certains d'entre vous l'ont remarqué, les équations (9) forment deux équations pour $$ \frac{d \dot V}{dt}, \frac{d \dot N}{dt},$$ laissant penser à deux équations du second degré. Il faut en fait ignorer les points et considérer deux équations du premier degré: $$ \frac{d V}{dt},\frac{d N}{dt}.$$

Vous pouvez vous inspirer de la structure du code vu en classe pour le modèle de FitzHugh-Nagumo fitzhugnagumo.m. Le fichier simule_morrislecar.m peut contenir la fonction morrislecar en fonction imbriquée. Le fichier simule_morrislecar aura cette structure:

function sol = simule_morrislecar()
% SIMULE_MORRISLECAR modele neurone de Morris-Lecar

% >>> ici les parametres du modele

% >>> ici simulations du modele

% >>> ici sorties graphiques

    % fonction morrislecar imbriquee
    function dxdt = morrislecar(t,x)
    % MORRISLECAR equations du modele neurone de Morris-Lecar

        % >>> ici equations et fonctions auxiliaires

    end

end

Testez en calculant la solution des équations avec les paramètres définis ci-dessus. Pour cela, utilisez ode23 ou ode45:

sol = ode23(@morrislecar(t,x),tspan,IC,options);

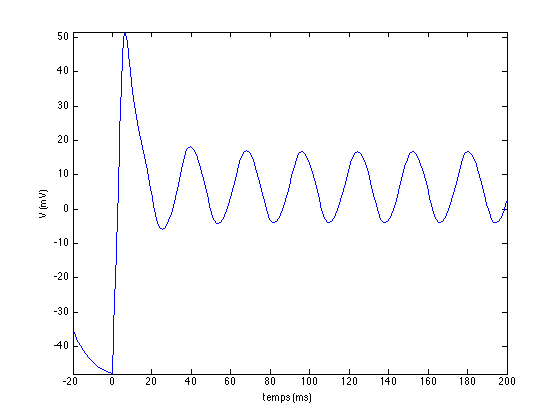
Comparez votre solution avec la figure ci-dessous. Pour obtenir cette figure, le courant appliqué vaut 0 pour les temps négatifs et I entre t = 0 et 200 ms.

figure(1); clf;
plot(sol.x,sol.y(1,:))
xlabel('temps (ms)')
ylabel('V (mV)')
axis tight

(Non noté) Vous pouvez vérifiez que vos solutions sont numériquement précises en comparant vos solutions avec des avec une solution calculée avec une tolérance très petite. La commande odeset permet de modifier les tolérance à l'erreur pour les solutions d'EDO. Les tolérances par défaut sont de 1e-3 pour l'erreur absolue et 1e-6 pour l'erreur relative. L'erreur relative joue quand les solutions sont grandes en valeurs absolues, tandis que l'erreur absolue joue quand les solutions sont proches de zeros. Par exemple, utilisez une tolérance absolue de 1e-9 et une tolérance relative de 1e-6 pour tester la précision de vos solutions.

options = odeset('AbsTol',1e-9,'RelTol',1e-6);
sol = ode23(@morrislecar,tspan,IC,options);
figure(1);
hold on
plot(sol.x,sol.y(1,:),'r--')

Q3 - Nullclines 5 pts

Calculez les nullclines pour V et W et tracez-les dans la figure 2 pour I = 100, 200, ... 500. Pour chaque intensité de courant tracez dans la figure 3 la solution V pour tspan = [0, 200]. Que remarquez-vous ? Vous devriez obtenir des résultats similaires à la figure 9 du papier de Morris et Lecar.

Q4 - Diagramme de bifurcation

Dans l'exercice 3, vous devriez avoir obtenu, pour certaines valeurs de I, des solutions oscillantes. Pour mieux caractériser ces solutions, vous allez tracer un diagramme de bifurcation.

On définit le paramètre de bifurcation comme le paramètre du modèle qui variera de façon continue. Pour une valeur donnée du paramètre de bifurcation, on trace sur le diagramme de bifurcation les points fixes. Par un argument de continuité, on s'attend en général à ce qu'un point fixe varie continuement en fonction du paramètre de bifurcation. Quand il ne le fait pas, ou que sa stabilité change, on a affaire à une bifurcation. Les points fixes stables sont tracés en ligne continues, et les points fixes instables en ligne discontinues. Pour les solutions périodiques, on trace les maxima et les minima de la solution (tous les extrema, y compris les extrema locaux).

A) 3 pts Commencez à tracez le diagramme de bifurcation dans la figure 4, avec I comme paramètre de bifurcation. Faites varier les valeurs de I entre 100 et 500 dans une boucle for. Pour chaque valeur de I, calculez les extrema de la solution du système de Morris-Lecar est tracez-les sur la figure en fonction de I

figure(4); clf;
for { I allant de 100 a 500 } 
    % Calculer la solution à I fixé, sur une durée suffisament longue
    % Obtenir les max et les min de la solution, après avoir enlevé
    %   les solutions transitoires. 
end
plot(I,{ max sol },'k',I,{ min sol },'k');
xlabel('parametre de bifurcation I (muA/cm2)')
ylabel('potentiel V (mV)')

B) 3 pts Pour chaque solution périodique, il existe aussi une solution d'équilibre, instable. Pour la déterminer, il faut résoudre un systeme d'équations non-linéaires: 0 = morrislecar(t,x). Pour ce faire utilisez une fonction anonyme de la forme suivante:

eq_stst = @(x) sum(morrislecar(0,x).^2);

Cette nouvelle fonction, eq_stst, renvoie la somme des carrés des membres de gauche des équations Morris-Lecar. En trouvant eq_stst = 0, on résoud le problème de point fixes. La commande fminsearch permet de trouver les valeurs de x pour lesquelles eq_stst(x) = 0. Faites varier I entre 100 et 500, comme en A), et touvez, pour chaque valeur de I, l'état d'équilibre x_stst des équations. Pour que fminsearch converge rapidement vers le point fixe, il faut donner une estimation initiale proche du point fixe. Vous pouvez utiliser comme estimation initiale la valeur du point fixe calculée à pour la valeur du paramètre I précédente. Pour la première estimation initiale, utiliser x0 = [-16, 0.13].

for { I allant de 100 a 500 } 
    % Calculer le point fixe x_stst solution de eq_stst = 0
    %   à I fixé, en utilisant le x_stst précédent comme estimation 
    %   initiale.
end
figure(4); 
hold on
plot(I,x_stst(1,:),'k--') % plot le premier élément de x_stst en traits discontinus

Vous devriez avoir obtenu un diagramme similaire à celui-ci

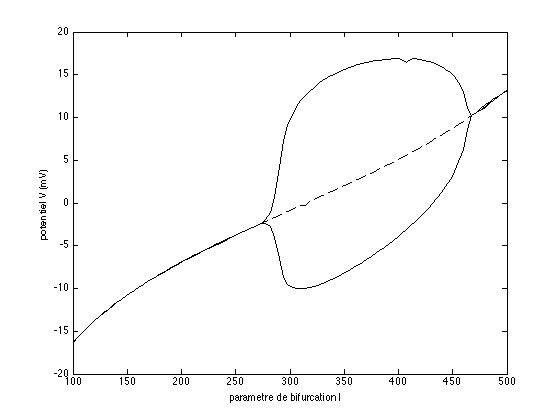
Q5 - Perturbations des paramètres 2 pts

Reprenez la figure 10 du papier, et reproduisez-la en figure 6. Le paramètre $\tau_K$ correspond à T0.

% panneau a)
g_Ca = 8;
% panneau b)
V3 = 12;
% panneau c)
T0 = 30;
% panneau d)
g_L = 1;

Q6 - Activité pacemaker BONUS

On change les paramètres V1 et V3, qui déterminent le potentiel de membrane pour lequel la moitié des canaux Ca++ et K+ sont ouverts. On met I = 50.

V1 = -1;
V3 = 10;
I = 50;
duree = 1000;

Maintenant, les canaux Ca++ sont activés à des voltages inférieurs à ceux de K+. Quelle est la dynamique du modèle? (Utilisez tspan = [0,1000] comme dans la figure 11 du papier).

Comparez votre solution avec la figure 11 du papier. Que concluez-vous ? Est-ce possible de reproduire la figure 11 ?