Modèles Integre-et-Tire et Modèles de Phase

Modèle d'Izhikevich, méthode d'Euler explicite (Forward Euler)

Les équations: $$C \frac{dv}{dt} = k ( v - vr ) ( v - vt ) - u + I,$$ $$\frac{du}{dt} = a( b ( v - vr ) - u ).$$ Si la variable $v$ atteint la valeur $v_{peak}$ au temps $t_{peak}$: $v(t) \to v_{peak}$ quand $t \to t_{peak}$, alors $v$ est remise à $v(t) = c$, et la variable $u$ est remise à $u(t)=u+d$.

Le modèle est paramétré de la façon suivante:

% parametres du modele
C=100; vr=-60; vt=-40; k=0.7;
a=0.03; b=-2; c=-50; d=100;
vpeak=35;
% parametres d'integration
T=1000; dt=1;
n=round(T/dt);
v=vr*ones(1,n); u=0*v;
I=[zeros(1,0.1*n),70*ones(1,0.9*n)];

% boucle principale: methode d'Euler
for i=1:n-1
    % Integre (etape Euler)
    v(i+1) = v(i) + dt * (k*(v(i)-vr)*(v(i)-vt)-u(i)+I(i))/C;
    u(i+1) = u(i) + dt * a*(b*(v(i)-vr)-u(i));

    % Tire (reinitialisation)
    if v(i+1) >= vpeak
        v(i)   = vpeak;
        v(i+1) = c;
        u(i+1) = u(i+1)+d;
    end
end

plot(dt*(1:n),v,'g');

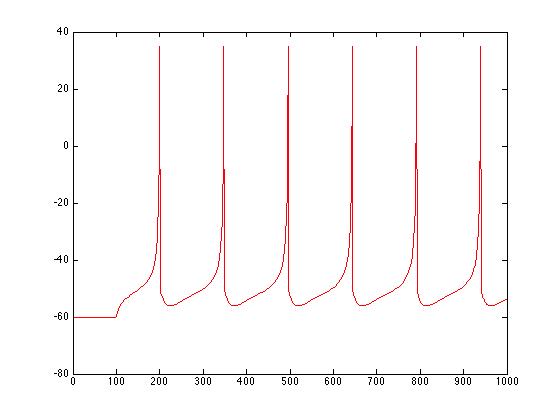
Modèle d'Izhikevich, méthode "Event Locator"

La fonction d'Izhikevich implémente le modèle intègre-et-tire avec la méthode "Event Locator".

sol = izhikevich;

Le code de la fonction izhikevich est

function sol = izhikevich
% IZHIKEVICH modele neurone integre-et-tire
% parametres des equations

C=100;
vr=-60;
vt=-40;
k=0.7;
a=0.03;
b=-2;
intensite = 70;
vpeak=35;
c=-50;
d=100;

% options de ode
% l'option 'Events' permet de gerer des evenements
% les ... permettent de continuer l'expression sur la ligne suivante
options = odeset('Events',@it_event, ...
               'AbsTol',1e-6, ...
               'RelTol',1e-3);
% conditions initiales
CI = [vr; 0];
% parametres de simulation
tfinal = 1000;
t0 = 0;
tout = t0;
xout = CI';
teout = [];
xeout = [];
while t0<tfinal
    [t,x,te,xe] = ode45(@it,[t0 tfinal],CI,options);
    nt = length(t);
     % on accumule les solutions
     tout = [tout; t(2:nt)];
     xout = [xout; x(2:nt,:)];
     teout = [teout; te];
     xeout = [xeout; xe];       % on met a jour t0
     t0 = t(nt);                % on met a jour les CI
     CI = [c; x(nt,2)+d];
end
 
% on affiche la solution pour v [x(1)]
plot(tout,xout(:,1),'r')
% on met la solution dans une structure de sortie
sol.t = tout;
sol.x = xout;
sol.te = teout;
sol.xe = xeout;

    %--------------------------------------------------------
    % Fonctions imbriquees
    %--------------------------------------------------------
    function dxdt = it(t,x)
    % IZ equations EDO         
    
        v=x(1);
        u=x(2);
        dxdt = [(k*(v-vr).*(v-vt)-u+input_current(t))/C;
                   a*(b*(v-vr)-u)];

    end     
    
    function I = input_current(t)
    % INPUT_CURRENT courant applique a la membrane         
    
        I = intensite * ( t>=(0.1*tfinal) );     
        
    end     
    
    function [value,isterminal,direction] = it_event(~,x)
    % IZ_EVENT detecte les evenements         
    
        value = x(1)-vpeak;
        isterminal = 1;
        direction = 1;     
        
    end

end

Modèle de phase

On peut identifier un point sur un cycle limite avec une phase, entre 0 et $2 \pi$.

Le modèle de phase le plus simple, représente en coordonnees polaires est

$$\frac{d\phi}{dt} = f(\phi),$$ si $\phi >= 2 \pi$, alors $\phi=0$ avec $f(\phi)$ (strictement) positive.

La phase est discontinue, mais, représentée en coordonnées cartésiennes, on obtient une hauteur $y = \sin(\phi)$ continue. Pour compléter, on peut tracer le portrait de phase avec $x = \cos(\phi)$ et $y = \sin(\phi)$.

Modèle de phase avec relaxation

En plus de la phase, on peut inclure l'amplitude comme variable dynamique. Cette deuxieme variable, $r$, est positive et est régie par l'équation

$$\frac{dr}{dt} = g(r,\phi).$$

L'équation de phase devient dependante de l'amplitude $$\frac{d\phi}{dt} = f(r,\phi).$$ si $\phi >= 2 \pi$, alors $\phi=0$

On obtient alors, en coordonnees cartesiennes, $$x = r \cos(\phi),$$ $$y = r \sin(\phi).$$

Exercice 1

Comparez les solutions du modèle d'Izhikevich obtenues avec la methode d'Euler et la methode 'Event Locator'. Quelle methode est la plus precise? Comment s'assurer que la solution obtenue est precise? Comparez les temps d'execution de chaque methode. Variez le pas de temps dt et les les parametres AbsTol et RelTol.

Exercice 2

En utilisant la methode de resolution de votre choix, tracez le portrait de phase du modèle d'Izhikevich (tracez u contre v). Localisez les points de discontinuite.

Exercice 3

Codez une methode pour resoudre l'équation de phase suivante: $$\frac{d\phi}{dt} = \omega (1.01+\sin(\phi)).$$

Utilisez le parametre omega=1.0, la condition initiale CI = 0.0, pour des temps entre 0 et 200. Pour la methode numerique, inspirez-vous, c.-a-d. copiez et modifiez, une des deux methode pour le modèle d'Izhikevich. Tracer la solution en coordonnees cartesiennes. Utilisez la fonction comet pour tracer la trajectoire dans le plan de phase (x,y).

Exercice 4

a) Codez une methode pour resoudre l'équation de phase suivante:

$$\frac{dr}{dt} = - \lambda (r-A),$$ $$\frac{d\phi}{dt} = \omega.$$

avec les paramètres lambda = 0.001, 0.01, 0.1, A = 1, et omega = 2*pi/100, pour t entre t = 0 et t = 1000. Resolvez pour des conditions initiales phi0 = 0, r0 = 0.1, 1.0, 2.0. Tracer les solutions en coordonnees cartesiennes.

b) Modifiez les équations pour inclure un terme de forcage dans la direction des x en coordonnees cartesiennes:

$$\frac{dr}{dt} = - \lambda (r-A) + F \cos(\phi) \cos\left(\frac{2 \pi}{T} t\right),$$ $$\frac{d\phi}{dt} = \omega - \frac{1}{r} F \sin(\phi)\cos\left(\frac{2 \pi}{T} t\right).$$

avec T = 50, 100, 200, et F assez petit.