How to make your Matlab code run 100x faster
Contents
An example: the Volterra Equation
The Volterra type II equation is a renewal equation
$$b(t) = f(t) + \int_0^t b(t-a) f(a) da$$where $b(t)$ is the birth rate at time $t$ needed for keeping the population constant in a population with instantaneous death rate of individuals aged $a$, $f(a)$.
Solving the Volterra equation numerically
We use the trapezoidal rule to discretize the integral term
$$t_i = i h, i = 0,1,...,N, h = \frac{t_{final}}{N},$$ $$b(t_i) = bi,$$ $$f(t_i-a_j) = f_{ij},$$ $$f(t_i) = f_i,$$ $$b_0 = f_0.$$and
$$(1-1/2 h f_{ii}) b_i = h \left(1/2 f_{i0} b_0 + \sum_{j-1}^{i-1} f_{ij} b_j\right) + f_i$$This is a linear system
$$A b = f$$with A a NxN matrix
$$A_{ii} = 1-1/2 h f_{ii}, i=1,...,N,$$ $$A_{ij} = -h f_{ij},$$ $$A_{i0} = -h/2 f_{i0},$$ $$A_{00} = 1.$$Once $A$ is determined, the Volterra equation is solved with the command
b = A\f
First implementation: MATLAB
Best use of vectorial notation
type volterra_mat.m
function A = volterra_mat(f,dt) % GENERATE_MATRIX lower triangular NxN matrix n = length(f); mf=repmat(f,1,n); A=spdiags(fliplr(mf'),-(n-1):0,n,n); A(:,1)=A(:,1)/2; A=A-diag(diag(A))/2; A(1,1)=0; A = speye(n)-dt*A;
Second implementation: MEX file (C source code)
Pure C code with two for loops
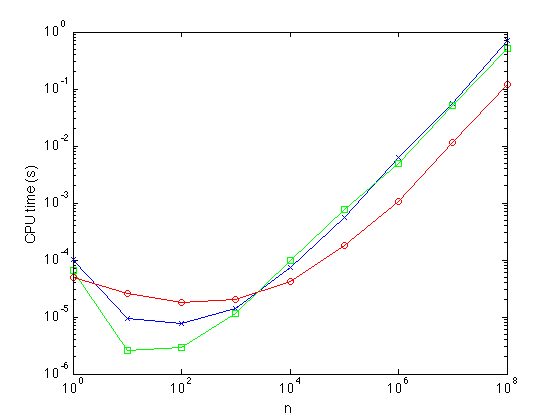
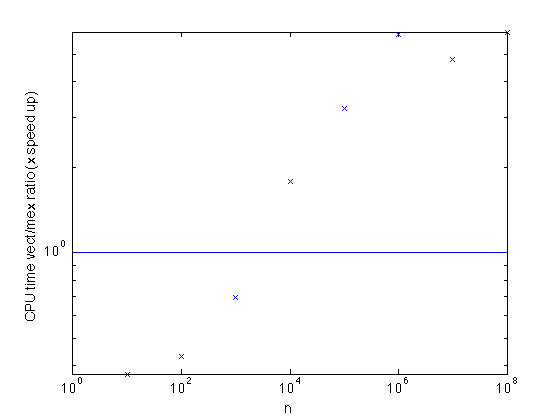
Speed test
clear; volterra_mat_test
speed ratio (matlab/mex): 0.11448 speed ratio (matlab/mex): 35.7465 speed ratio (matlab/mex): 50.0336 speed ratio (matlab/mex): 99.6 speed ratio (matlab/mex): 117.9858 speed ratio (matlab/mex): 56.8965 speed ratio (matlab/mex): 39.681 speed ratio (matlab/mex): 55.7403 speed ratio (matlab/mex): NaN speed ratio (matlab/mex): NaN
MEX files
Source code can be FORTRAN, C, C++
Example with C
void
mexFunction(int nlhs,mxArray *plhs[],int nrhs,const mxArray *prhs[])
{
...
}
mexFunction inputs:
- int nlhs: number of left-hand-side argument, or matlab outputs
- mxArray *plhs[]: pointer to an array of pointers correspondin to the matlab outputs. Array of size nlhs.
- int nrhs: number of right-hand-side argument, or matlab inputs
- const mxArray *prhs[]: pointer to an array of pointers corresponding to the matlab inputs. Array of size nrhs.
mxArray is the basic type of a matlab variable.
Here, the mex-file voltmat_mex takes two arguments (one vector f and one double dt) and returns a matrix A: nlhs = 1, nrhs = 2
{
mwSize mrows, ncols;
double *f; // the pointer to the vector f
double h; // timestep in the discretization f = mxGetPr(prhs[0]); // assign the pointer to the 1D array
mrows = mxGetM(prhs[0]); // get its length
ncols = mrows; // not really useful hereh = mxGetScalar(prhs[1]);
// create a mrowsxncols matrix
double *A = mxCalloc(mrows*ncols, sizeof(double));
// use mxCalloc instead of malloc // filling up the matrix A, to solve the Volterra equation as A*x = f
voltmat(A,f,h,mrows,ncols); // initialize the output
plhs[0]=mxCreateDoubleMatrix(0,0,mxREAL);
// this creates a pointer to an empty matrix of doubles (with real numbers) /* Point mxArray to A */
mxSetPr(plhs[0], A); // first output pointer to A
mxSetM(plhs[0], mrows); // assign the size of A
mxSetN(plhs[0], ncols); // assign the size of A// do not free A, since plhs[0] points to A
return; }
The actual C routine
void voltmat( double *A, double *f, double h, mwSize m, mwSize n )
{
mwIndex i,j;
for (j = 0; j < n; j++)
{
for (i = j; i < n; i++)
{
*( A+i+n*j ) = - *(f + i - j) * h;
}
}
*A = 0;
for (i = 0; i < m; i++)
{
*(A + i) = *(A + i)/2;
}
for (i = 0; i < m; i++)
{
*(A + i*(n+1) ) = 1 + *(A + i*(n+1))/2;
}
}The full C source code
type voltmat_mex.c
/* VOLTMAT_MEX generates a Volterra matrix from the vector f
* To compile:
* mex -O -v voltmat_mex.c
*
* mandatory input arguments:
* f: column vector of doubles of length m
* h: timestep (double scalar)
*/
/* always include mex.h, it contains the Matlab types */
#include "mex.h"
/* #include "matrix.h" */
/* voltmat takes an array of doubles f, a double h, and returns a matrix A */
void voltmat( double *A, double *f, double h, mwSize m, mwSize n )
{
mwIndex i,j;
for (j = 0; j < n; j++)
{
for (i = j; i < n; i++)
{
*( A+i+n*j ) = - *(f + i - j) * h;
}
}
*A = 0;
for (i = 0; i < m; i++)
{
*(A + i) = *(A + i)/2;
}
for (i = 0; i < m; i++)
{
*(A + i*(n+1) ) = 1 + *(A + i*(n+1))/2;
}
}
void
mexFunction(int nlhs,mxArray *plhs[],int nrhs,const mxArray *prhs[])
{
mwSize mrows, ncols;
double *f; /* the pointer to the vector f */
double h; /* timestep in the discretization */
f = mxGetPr(prhs[0]); /* assign the pointer to the 1D array */
mrows = mxGetM(prhs[0]); /* get its length */
ncols = mrows; /* not really useful here */
h = mxGetScalar(prhs[1]);
/* create a mrowsxncols array */
double *A = mxCalloc(mrows*ncols, sizeof(double));
/* filling up the matrix A,
* to solve the Volterra equation as A*x = f
*/
voltmat(A,f,h,mrows,ncols);
/* initialize the output */
plhs[0]=mxCreateDoubleMatrix(0,0,mxREAL);
/* Point mxArray to A */
mxSetPr(plhs[0], A);
mxSetM(plhs[0], mrows);
mxSetN(plhs[0], ncols);
/* Do not free A, since the output plhs[0] points to A */
return;
}
Compiling
First setup the mex compiler. This step is OS-dependent, see Matlab documentation by typing
mex -help
and then compile
mex -O voltmat_mex.c
add the -v switch to display compilation details
This creates a matlab executable file. On MacOS, it has an extension .mexmaci64
The executable can be called as any other Matlab function.
Caveat
Mex-files are pre-compiled, if you have bugs, Matlab will not be able to tell you where the error is.
You cannot interrupt execution of a mex-file from within Matlab (Ctrl-C does not work). To stop the execution, you need to kill Matlab, so make sure you properly save your data before launching possibly long simulations.
It is possible to use debugger tools, but this is for another tutorial.
Second example: The sum of the first N integers
Vectorized notation
type sum_first_n_vect.m
function s = sum_first_n_vect(n) % SUM_FIRST_N_VECT sums the first N integers, vectorial form s = sum(1:n);
Loop notation
type sum_first_n_loop.m
function s = sum_first_n_loop(n)
% SUM_FIRST_N_LOOP sums the first N integers, loop form
s = 0;
for i=1:n
s = s + n;
end
mex code
type sum_first_n_mex.c
/* SUM_FIRST_N_MEX sums the first N integers
* To compile:
* mex -O -v sum_first_n_mex.c
*
* mandatory input arguments:
* integer N
*/
/* always include mex.h, it contains the Matlab types */
#include "mex.h"
void
mexFunction(int nlhs,mxArray *plhs[],int nrhs,const mxArray *prhs[])
{
int n;
double *s;
int i;
n = (int)mxGetScalar(prhs[0]);
/* initialize the output */
plhs[0]=mxCreateDoubleMatrix(1,1,mxREAL);
s = mxGetPr(plhs[0]);
*s = 0;
for (i = 1; i <= n; i++)
{
*s += i;
}
return;
}
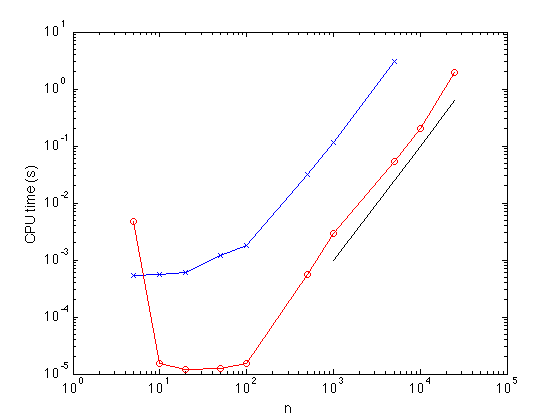
CPU times
clear sum_first_n_test
speed ratio (matlab/mex): 2.0149 speed ratio (matlab/mex): 0.37371 speed ratio (matlab/mex): 0.42946 speed ratio (matlab/mex): 0.69378 speed ratio (matlab/mex): 1.7844 speed ratio (matlab/mex): 3.2112 speed ratio (matlab/mex): 5.8532 speed ratio (matlab/mex): 4.7788 speed ratio (matlab/mex): 5.9796