- A rendre le 4 février 2015 en début de séance
- Chaque étudiant doit rendre une copie, en PDF ou en version papier
- Joindre les codes utilisés pour produire les résultats numériques
L'objectif du DM est d'étudier le modèle deux EDO nonlinéaires présenté par Kuznetsov et collègues dans l'article suivant
Kuznetsov VA, Makalkin IA, Taylor MA, Perelson AS, Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis (1994) Bull Math Biol 56:295-321
Les codes dans immunogeneic_tumor_growth sur github peuvent vous être utiles.
Exercice 1 - Le modèle
1 Décrivez les concepts de "tumor dormancy", "sneaking through mechanisms" et de "immunostimulation effects"
2 Le modèle initial se compose de cinq EDO nonlinéaires pour les variables $(E, T, C, E^*, T^*)$. Les auteurs font des simplifications pour obtenir un modèle avec seulement deux variables $(E,T)$. Décrivez les étapes suivies et les hypothèses utilisées pour réduire le modèle.
3 Le modèle est ensuite adimensionalisé pour obtenir un modèle sur $(x,y)$ décrit par les équations.
\begin{align} \frac{dx}{d\tau} & = \sigma + \rho \frac{xy}{\eta + y} - \mu x y - \delta x, \\ \frac{dy}{d\tau} & = \alpha y (1 - \beta y) - x y. \end{align} avec les valeurs de paramètres| Paramètre | Expression | Valeur |
|---|---|---|
| $\tau$ | $n T_0 t$ | - |
| $x$ | $\frac{E}{E_0}$ | - |
| $y$ | $\frac{T}{T_0}$ | - |
| $T_0, E_0$ | - | $10^{6}$ cellules |
| $\sigma$ | $\frac{s}{n E_0 T_0}$ | $0.1181$ |
| $\rho$ | $\frac{p}{n T_0}$ | $1.131$ |
| $\eta$ | $\frac{g}{T_0}$ | $20.19$ |
| $\mu$ | $\frac{m}{n}$ | $0.00311$ |
| $\delta$ | $\frac{d}{n T_0}$ | $0.3743$ |
| $\alpha$ | $\frac{a}{n T_0}$ | $1.636$ |
| $\beta$ | $\frac{b}{b T_0}$ | $2.0 \times 10^{-3}$ |
Vérifiez les calculs de changement d'échelle et d'adimensionalisation
Exercice 2 - Équilibres
On cherche à identifier et caractériser les états d'équilibre (points fixes) du modèle. Pour conserver le réalisme biologique du modèle, on cherche les états d'équilibre non-négatifs $(x \leq 0, y \leq 0)$, pour des paramètres non-négatifs (aucun des paramètres n'a de sens pour des valeurs négatives).
1 Les isoclines sont des courbes (ou des variétés) dans l'espace de phase pour sur lesquelles $\dot x$ ou $\dot y$ sont constantes. Les isoclines de niveau zéro (nullcline en anglais) sont les courbes qui satisfont $\dot x = 0$ et $\dot y = 0$. Les points d'intersection des isoclines sont des points fixes. Déterminez les isoclines et tracez leurs graphes (numériquement) pour des valeurs de paramètres données dans la figure 2 de l'article: cas avec quatre, deux et un points fixes en faisant varier $\beta$. En déduire que le modèle possède entre un et quatre points fixes.
2 Les points fixes sont donnés par deux équations: un polynôme de degré 3 et une équation linéaire. Déterminez ces deux équations et identifiez les points fixes non-négatifs possibles.
3 La règle des signes de Descartes est une règle simple pour déterminer une borne supérieure sur le nombre de racines réelles positives d'un polynôme à coefficients réels. On ordonne les coefficient par ordre décroissant de degré. Le nombre de racines positives est ou bien égal au nombre de changement de signes des coefficients, ou est inférieur par un multiple de 2. Les racines multiples sont comptées séparément.
En fonction des signes des coefficients du polynôme de degré 3, donnez le nombre maximal de points fixes positifs.
Exercice 3 - Portrait de phase
On cherche à établir les portaits de phase du modèle. Pour cela, il faut dans un premier temps trouver les points fixes, caractériser leur types (col, noeud, foyer), et leur stabilité. Dans un deuxième temps il faut déterminer les variété stables et instables. En particulier, une variété stable partitionne l'espace de phase en deux, de sorte que les toutes les trajectoires sont contenues dans une de ces deux parties.
1 Portrait de phase avec paramètres par défaut. Tracez le portrait de phase du modèle avec les paramètre par défaut. Suivez les étapes
- Déterminez (numériquement) les valeurs des quatres points fixes (nommez-les $A, B, C, D$ comme dans l'article).
- Linéarisez le modèle autour de chacun de ces points fixes. (Déterminez la matrice Jacobienne du modèle (pour $(x,y)$ quelconque) et évaluez-la en ($A, B, C, D$).
- Calculer les valeurs propres et vecteurs propres associées pour chaque point fixe.
- Caractérisez (stabilité asymptotique et type) chaque point fixe.
- Tracez dans l'espace de phase quelques trajectoires bien choisies (essayez de d'atteindre tous les points fixes stables et de couvrir une bonne partie de l'espace).
- Tracez les variétés stables et instables des points col. (Il n'est pas utile de représenter les variétés pour les autres types de points fixes). Pour ce faire, utilisez l'information donnée par les vecteurs propres du linéarisé. Soit $p \in \mathbb{R^2}$ un point col avec $\lambda_1 < 0$, $\lambda_2 > 0$, et $v_1$ $v_2$ les vecteurs propres associés. Alors, dans un voisinage de $p$, les variétés stables et instables sont alignées avec les sous-espace stables et instables du linéarisé, dont les directions sont données par les vecteurs propres. Pour tracer la variété instable, on peut prendre une condition initiale sur le sous-espace instable: $p \pm \epsilon v_2$, avec $\epsilon > 0$ petit.
Exercices 4 Bifurcations
On prend le parametre $\mu$ comme paramètre de bifurcation.
1 Diagramme de bifurcation. Tracez le diagramme de bifurcation du modèle en fonction de $\mu$ (un diagramme pour $x$ et un pour $y$.) Vous devriez obtenir une figure semblable à celle-ci:
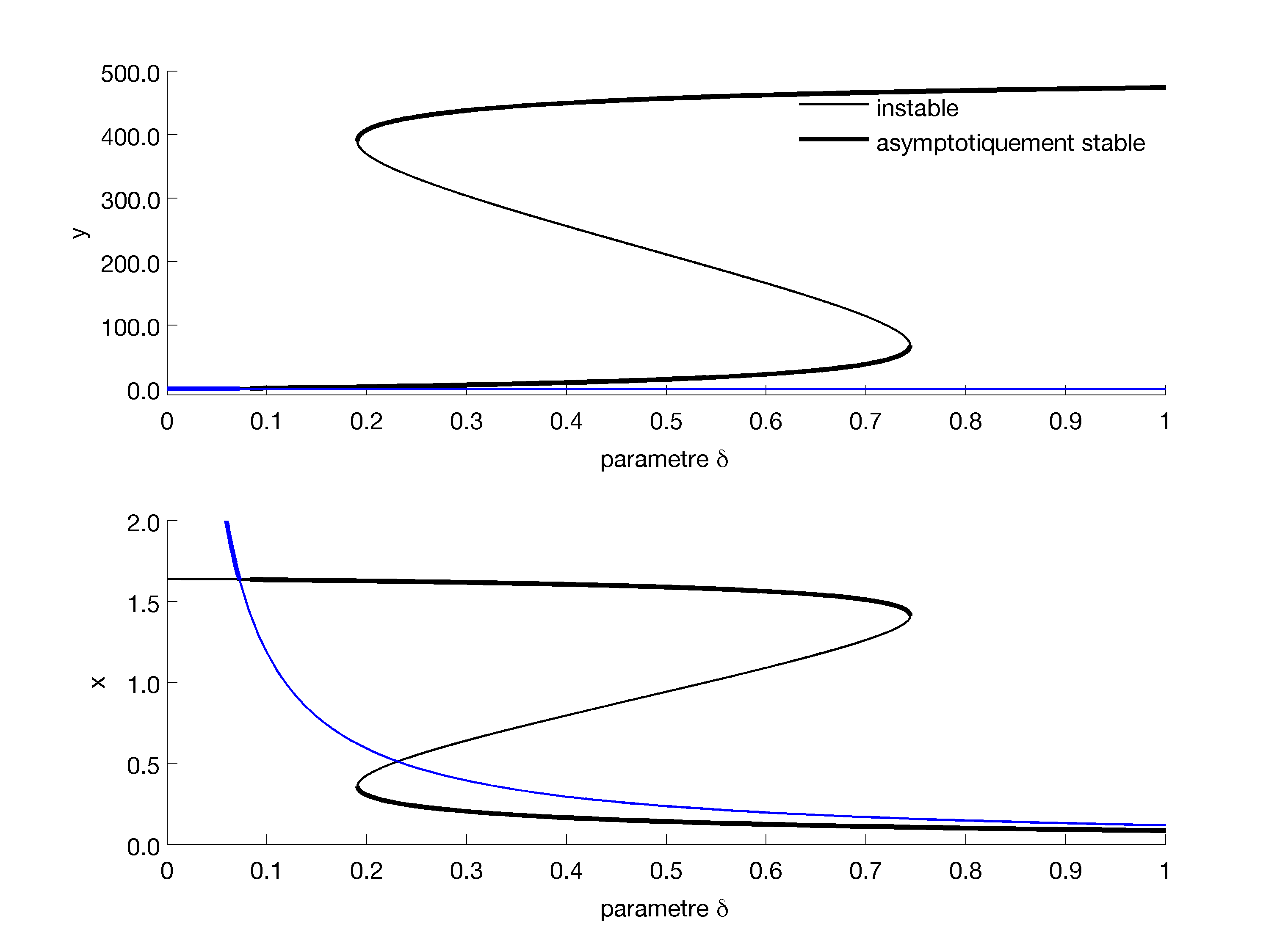
Identifiez les bifurcations rencontrées.
Exercice 5 Bifurcation hétérocline
La bifurcation hétérocline ne peut être détectée localement. En faisant varier $\delta$, tracez les variétées instable du point fixe A et la variété stable du point fixe C, jusqu'à ce qu'elles coïncident. Quelle est l'effet d'une bifurcation hétérocline sur le portrait de phase ?
Exercice 6 Simulations stochastique
Ecrivez le modèle sous forme d'un processus de naissance et de mort. Pour le passage au discret, on prendra un volume isolé $\Omega$ tel que le nombre de cellules dans le système est $N_x = \Omega x$ et $N_y= \Omega y$.
- Listez tous les événements possibles (naissance/mort) et indiquez le taux d'occurence de l'événement.
- Codez le modèle avec l'algorithme stochastique.
- Simulez le modèle à plusieurs reprises, avec différentes conditions initiales.