The aim of this assignment is to study the two-dimensional ODE system presented by Kuznetsov and colleagues in the article

Kuznetsov VA, Makalkin IA, Taylor MA, Perelson AS, Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis (1994) Bull Math Biol 56:295-321

Exercise 1 - The model

1. Describe the concepts of "tumor dormancy", "sneaking through mechanisms" and "immunostimulation effects". Use the description from the article, but also from other sources (give the references).

2. The initial model is made of five nonliear ODEs with variables $(E, T, C, E^*, T^*)$. The authors make simplifications to obtain a model with two variables only, $(E,T)$. Describe the steps followed and the hypotheses used to reduce the model.

3. The model is then non-dimensionalised, and the authors obtain a model on $(x,y)$ with the equations

\begin{align} \frac{dx}{d\tau} & = \sigma + \rho \frac{xy}{\eta + y} - \mu x y - \delta x, \\ \frac{dy}{d\tau} & = \alpha y (1 - \beta y) - x y. \end{align} and parameter values
Parameter	Expression	Value
$\tau$	$n T_0 t$	-
$x$	$\frac{E}{E_0}$	-
$y$	$\frac{T}{T_0}$	-
$T_0, E_0$	-	$10^{6}$ cells
$\sigma$	$\frac{s}{n E_0 T_0}$	$0.1181$
$\rho$	$\frac{p}{n T_0}$	$1.131$
$\eta$	$\frac{g}{T_0}$	$20.19$
$\mu$	$\frac{m}{n}$	$0.00311$
$\delta$	$\frac{d}{n T_0}$	$0.3743$
$\alpha$	$\frac{a}{n T_0}$	$1.636$
$\beta$	$\frac{b}{b T_0}$	$2.0 \times 10^{-3}$

Check that the change of scale and non-dimensionalisation works.

Exercise 2 - Steady states

We want to find and characterise the steady states of the model. To preserve biological realism of the model, we are looking for non-negative steady states (0 included) $(x \geq 0, y \geq 0)$, for non-negative parameter values.

1. Nullclines are curves (or manifolds) in the phase space for which $\dot x = 0$ ou $\dot y = 0$. Intersection points of the nullclines are steady states. Determine the nullclines and plot their graphs (numerically) for the parameters values given in Fig 2 of the article: the case with four, deux and one steady states, by varying the parmater $\beta$. Conclude that the model possesses between one and four steasy states.

   Remark that the parameter to vary is $\beta$, not $\rho$. This question requires only numerical exploration.

2. The steady states are given by two equations: a cubic polynomial and a linear equation. Determine these two equations.

3. §

   The Descartes rule of signs is a simple rule to determine how many positive real roots a polynomial can have. First sort the coefficients by decreasing degrees. The number of positive root is equal to the number of sign changes in the coefficient, or is less than that by a multiple of 2. Multiple root are counted separately.

   Given the parameters of the cubic polynomial, determine the maximal number of positive steady states.

Exercise 3 - Phase portrait

We now try to establish the pahse protrait of the model. To do this, we need first to determine the steady states, and characterise their types: (saddle, node, focus, ...). and their stability. Second, we need to determine the stable and unstable manifolds. In particular, the stable manifold of a saddle will separate the phase space into two part, so that ewvery trajectory is completely contained in one of those parts.

1 Phase portrait with defautl parameters. Plot the phase protrait with default model parameters. Follow the steps:

• Find numerically the four steady states (label them $A, B, C, D$ as in the article).
• Linearise the model around each of the steady states. (Determine the Jacobian matrix for any $(x,y)$ and evaluate it at ($A, B, C, D$).
• Compute the eigenvalues and the eigenvectors associated to each steady state.
• Characterise (asymptotic stability and type) of each steady state.
• Plot in the phase space a few selected trajectories (try to select trajectories that cover most of the phase spaces are reach the stable steady states).
• Plot the stable and unstable manifolds of the saddles. (No need to plot the manifolds for the other type of steady states). To do that, use the information given by the eigenvectors of the Jacoban matrix. Let $p \in \mathbb{R^2}$ a saddle point with $\lambda_1 < 0$, $\lambda_2 > 0$, and $v_1$ $v_2$ the associated eigenvectors. Then, in a neighbourhood of $p$, the stable and unstable manifolds are tangent to the stable and unstable subspaces of the Jacobian, which are spanned by the eigenvectors. To plot the unstable manifold, you can take an initial condition on the corresponding linear subspace: $p \pm \epsilon v_2$, avec $\epsilon > 0$ small. To plot the stable manifold, you can take an initial condition on the corresponding linear subspace: $p \pm \epsilon v_2$, avec $\epsilon > 0$ small, and integrate in negative times.

You should get a figure similar to Fig 3 in the article.

You can use or adapt the codes immunogeneic_tumor_growth.m on immunogeneic_tumor_growth.

Exercises 4 Bifurcations

We choose parameter $\delta$ as the bifurcation parameter.

1 Bifurcation diagram. Plot the bifurcation diagram fo the model, with respect to $\delta$ (plot one diagram for $x$ and one for $y$.) You should obtaint something like

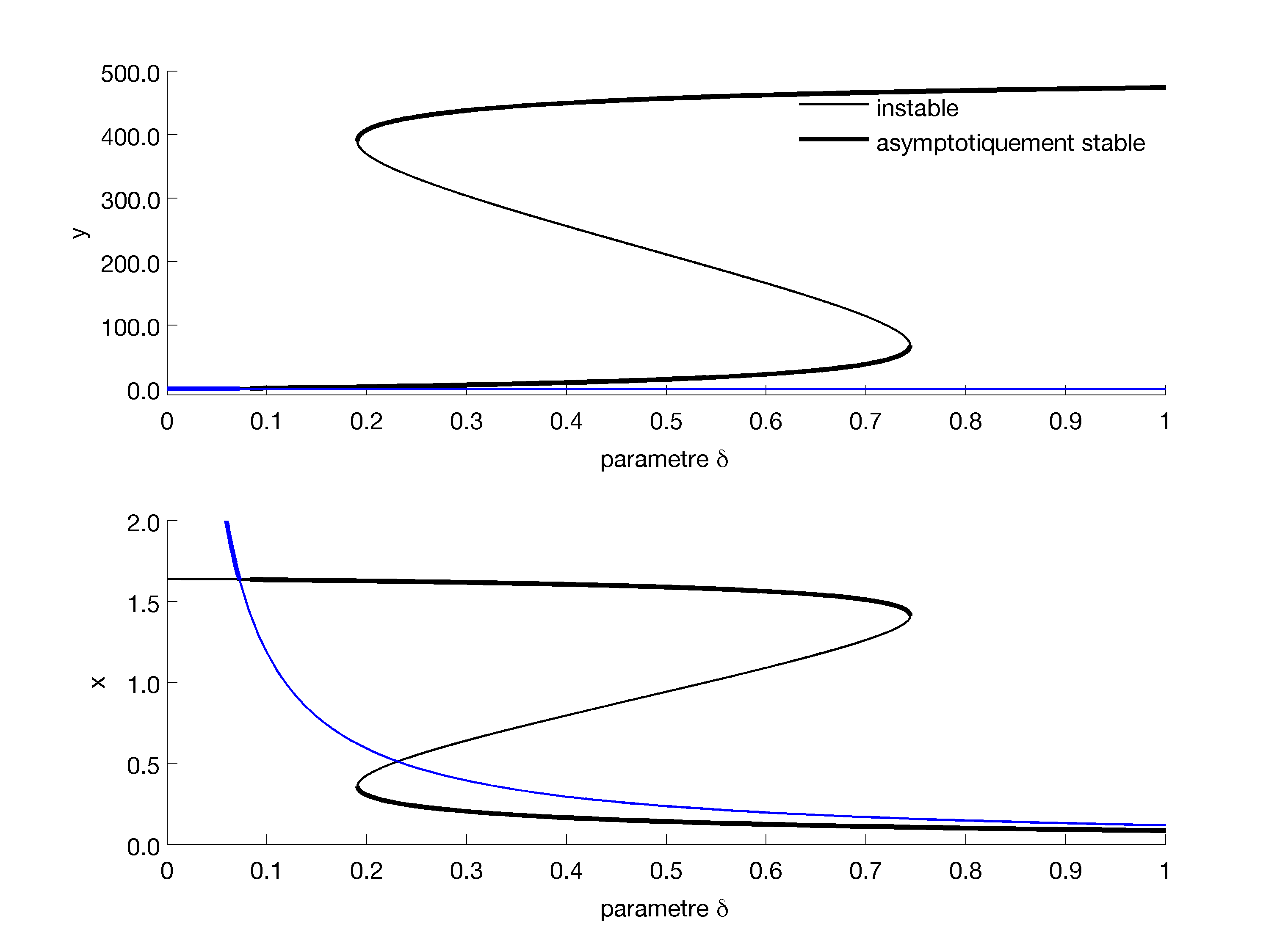
Characterise the bifurcations you see.

Exercise 5 Heteroclinic Bifurcations

The heteroclinic bifurcation cannot be detected locally. By varying $\delta$, plot the unstable manifold of the steady state A and the stable manifold of the steady state C until they coincide. What is the effect of the heteroclinic bifurcation on the phase portrait?

Exercise 6 Stochastic simulations

Write the model as a birth and death process. To convert to model to discrete values, we will use a reference volume $\Omega$ such that the number of cells in the system is $N_x = \Omega x$ and $N_y= \Omega y$. The volume $\Omega$ is a parameter of the birth and death process you will have to take into account.

• List all the possible birht death events, and provide the rate at which each event occurs.
• Implement the process with the Stochastic Simulation Algorithm (SSA).
• Simulate the process many times, with different initial conditions.

You can use or adapt the codes stoch_tumor_growth.m on immunogeneic_tumor_growth.

The typical cell number in the blood is on the order of 100 to 1000 per $\mu$L. To figure out what kind of simulation volume to use, first determine the cell number $N$ you want to simulate, 1, 10, 100, 1000?, and which concentration $C$ you want, 100, 1000? This will give you the required volume $\Omega = N/C$.

References

Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis