Dynamique des populations I

L'objectif du DM est d'étudier les modèles d'infection du système immunitaire par des virus.

Nowak, M. A., Bangham, C. R. (1996). Population dynamics of immune responses to persistent viruses. Science, 272, 74-79

Exercice 1 - Les modèles et les hyopthèses

Q1 Donnez une courte description des termes utilisés dans l'article:

a) Okham's razor
b) Cytotoxic T lymphocytes (CTL)
c) CTL responsivness
d) Basic reproductive ratio $R_0$
e) Equilibrium diversity
f) Epitope

Question bien réussie dans l'ensemble

Exercice 2 - Équilibres et stabilité

L'article présente trois modèles, de complexités croissantes: Virus replication (I), Immune responses reduce virus load (II), et Viral diversity and escape from immune response (III).

Modèle I - Virus replication

Dynamique de la réplication du virus sans réponse immunitaire.

Q2 a) De quel type est le point d'équilibre sans infection ?

Q2 b) Donnez une condition nécessaire et suffisante pour que le point d'équilibre sans infection soit asymptotiquement stable. Comparez avec la valeur $R_0$ trouvée en a).

Question bien réussie. Les valeurs propres de la matrices jacobienne au point fixe sont toutes réelles. Deux des valeurs propres sont toujours négatives. On a donc un noeud si les valeurs propres sont négatives et un point selle si on a une valeur positive.

Question bien réussie. Le point fixe sans infection $(\lambda/d, 0, 0)$ est asymptotiquement stable si et seulement si $R_0<1$. On obtenait une condition équivalente en imposant aux valeurs propres de la matrice jacobienne de ne prendre que des valeur négatives.

Q2 c) Si le point d'équilibre sans infection est instable, quel est le comportement asymptotique du système ?

Pour toutes les valeurs de paramètres admissibles, il existe deux points fixes. Le point fixe avec infection $(x^*,y^*,v^*)$ a des coefficients positifs quand $R_0>1$, c.-à-d. quand le point fixe sans infection est instable. Dans l'article, ce point fixe est décrit comme un foyer stable. Il s'agit ici de montrer que 1) ce point fixe est stable lorsque $R_0>1$, et 2) quelle trajectoires convergent vers ce point fixe.

Q2 d) Calcul du taux de reproduction de base $R_0$.

Maths en action seulement Première méthode:

Le taux de reporduction de base est donné dans l'article par $R_0 = \beta \lambda k / (d u a)$. Ce taux est le nombre moyen de nouvelles cellules infectées par un cellule infectée, quand le nombre de cellules infectées est petit. Définissons $R_0$ de la façon suivante: $$ R_0 = \int_0^\infty \beta x(t)v(t) dt,$$ où $x(t)$ est à l'équilibre sans infection, c.-à-d. au tout début de l'infection, quand le nombre d'infecté est négligeable, et où $v(t)$ est la quantité de virus produite par une seule cellule infectée. Pour trouver $R_0$, trouvez d'abord la probabilité pour une cellule infectée de survivre jusqu'au temps $t$, $p_y(t)$. La production virale moyenne uniquement due à une cellule infectée est donnée par $$ \dot v = k p_y(t) - uv.$$

Résolvez pour $v(t)$, avec condition initiale $v(0)=0$ et calculer l'intégrale pour $R_0$.

La durée de vie d'une cellule infectée est distribuée exponentiellement, et la probabilité qu'une cellule infectée soit vivante au temps $t$ est $p_y(t) = \exp(-at)$. La quantité de virus $v(t)$ produite par une cellule infectée est donnée par la solution de l'équation différentielle ci-dessus.

Deuxième méthode

En utilisant $x = \lambda / d$, $v = ky/u$, exprimez $\dot y/(ay)$, le taux relatif de nouvelles cellules infectées par durée de vie d'une cellule infectée, comme $$ \frac{\dot y}{a y} = R_0 - 1,$$ de façon à retrouver $R_0$.

Modèle II- Immune response

Dynamique de la réplication du virus avec réponse immunitaire.

Q2 e) Maths en action seulement En plus des deux points d'équilibre sans système immunitaire, il existe un troisième point d'équilibre pour $z$ non-nul (noté $\hat z$). Donnez une condition nécessaire et suffisante sur les paramètres pour que ce troisième point d'équilibre soit asymtotiquement stable. Vérifiez que cette condition est équivalente à $cy^* > b$, $x^* < \hat x$, ou $v^* > \hat v$.

Le point d'équilibre $\hat y = b/c$. La condition $cy^* > b$ dit essentiellement que $\hat y < y^*$, ou encore que $\hat z > 0$. Démontrer la stibilité de ce point fixe directement est difficile. La matrice Jacobienne est de taille 4x4 et peu de simplifications sont possibles. Une approche consiste à montrer que le point fixe * est instable. Une autre approche est de déterminer les valeurs propres pour des valeurs de paramètres bien choisies, et d'ensuite faire varier ces paramètres en s'assurant que les parties réelles des valeurs propres ne changent pas de signe. En prenant $\hat y = y^*$ et $\hat z = 0$,

Modèle III - Viral diversity

Diversité virale et échappement du système immunitaire.

Q2 f) Maths en action seulement Simulations numériques. Reproduisez les figures 3A-D. Utilisez le logiciel/langage de votre choix.

Q2 g) Maths en action seulement Etude de stabilité. \begin{align} \dot x & = \lambda - dx - x \sum_{i=1}^n \beta_i v_i, \\ \dot y_i & = \beta_i v_i - a y_i - p z_i y_i , \\ \dot v_i & = k_i y_i - u v_i \\ \dot z_i & = c y_i z_i - b z_i. \end{align}

Exercice 3 - Portrait de phase

Pour le master SITN, utiliser le modèle I pour les questions a) et b).

Q3 a) Tracez les portraits de phase dans le plan $yv$ quand le point d'équilibre sans infection est stable. Inclure les points d'équilibre négatifs.

Note du 3 février Il faut se baser sur les paramètres donnés dans l’article. Cependant, il est courant que toutes les valeurs de paramètre ne soient pas fournies dans les articles de recherche. Il faut donc choisir 2 jeux de paramètres, un pour le point d’équilibre avec infection instable, et un quand il est stable. Essayer de ne varier qu’un paramètre à la fois, en gardant le plus possible les paramètres proches de ceux fournis dans l’article.

Q3 b) Tracez les portraits de phase dans le plan $yv$ quand le point d'équilibre avec infection mais sans réponse immunitaire est stable. Inclure les points d'équilibre négatifs.

Q3 c) Maths en action seulement Tracez les portraits de phase dans le plan $vz$ quand le point d'équilibre avec réponse immunitaire est stable. Inclure les points d'équilibre négatifs.

Exercice 4 - Bifurcations

Pour cet exercice, on prend le modèle II (réponse immunitaire). Comme valeurs de paramètres, se baser sur les valeurs de la figure 2: $\lambda = 1$, $d = 0.01$, $a = 0.5$, $\beta k / u = 0.05$, $b = 0.05$, $p = 1$. Le paramètres de bifurcation sont la sensibilité du système immunitaire $c$ et le taux de mort des cellule infectées par la réponse immunitaire $p$.

Q4 a) Maths en action seulement Tracez les diagrammes de bifurcations correspondant à la figure 2, pour chacun des scénarios (Model 1, 2, 3). Inclure tous les points d'équilibre, incluant les points instables.

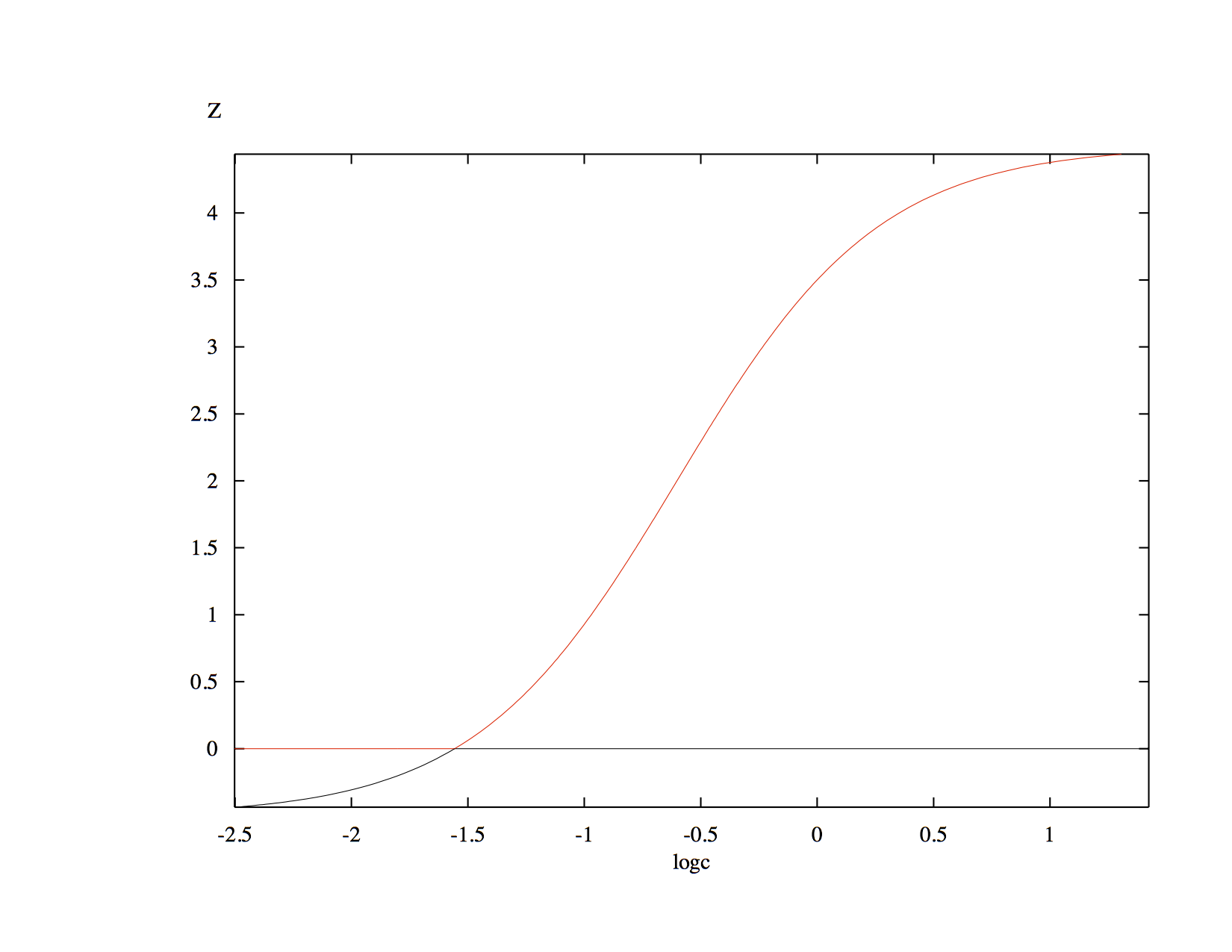
Note du 4 février. Voici un diagramme de bifurcation pour $z$ avec $c$ comme paramètre de bifurcation. Les paramètres utilisés sont: $\lambda=1,d=0.01,a=0.5,\beta=0.05,k=1,u=1,b=0.05,p=1$. Le paramètre $c$ varie entre $10^{-2.5}$ et $10^{1.2}$. Notez l'échelle log sur le diagramme. Ce diagramme a été calculé numériquement avec XPPAUT, mais il est possible de calculer le diagramme de bifurcation analytiquement. Les courbes en rouge représentent de points d'équilibre stables et les courbes en noir des points d'équilibre instables. Après quelques essais infructueux à faire fonctionner MATCONT, j'ai réussi à produire le même diagramme de bifurcation.

Pour les SITN, tracez le diagramme de bifurcation du modèle I avec, par exemple $\beta$ comme paramètre de bifurcation

Q4 b) identifiez toutes les bifurcations que vous voyez: type de bifurcation, pour quelles valeurs de paramètres et les changements dans le portrait de phase.

Exercice 5 - Simulations stochastiques

Q5 Maths en action seulement Ecrivez le modèle II sous forme d'un processus de naissance et de mort. Pour le passage au discret, on prendra un volume isolé $\Omega$ tel que les nombres de cellules dans le système est $N_r = \Omega r$ pour $r \in \{x,y,v,z \}$.

a) Listez tous les événements possibles (naissance/mort) et indiquez le taux d'occurence de l'événement.
b) Codez le modèle avec l'algorithme stochastique.
c) Simulez le modèle à plusieurs reprises, avec différentes conditions initiales.

Référence

Nowak, M. A., Bangham, C. R. (1996). Population dynamics of immune responses to persistent viruses. Science, 272, 74-79