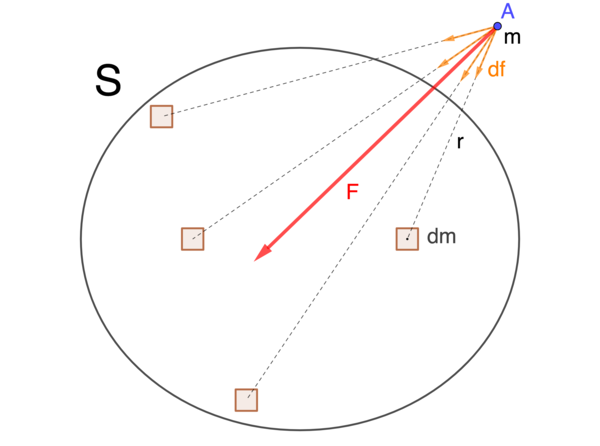

On décompose S en petits objets élémentaires, des cubes par exemples, que l'on peut assimiler à des objets ponctuels. Pour chaque cube on calcule l'attraction élémentaire df qu'il exerce sur M en remplaçant, dans la formule de la Gravitation Universelle, M1 par le centre du cube, m1 par la masse dm de ce cube, M2 par A et m2 par m. La force de gravitation F exercée par S sur M est la somme de toutes les attractions élémentaires. On ne les a bien sûr pas toutes représentées sur la figure, pour une meilleure visibilité.
En réalité la somme ainsi calculée dépend du découpage choisi. Mais on peut démontrer qu'en choisissant des cubes de plus en plus petits on obtient des sommes de plus en plus proches d'un même vecteur limite. C'est cette limite qui, par définition, est l'attraction F exercée par S sur M.
Si on double, par exemple, la masse m de M, chacune des attractions élémentaires df est doublée, et donc aussi leursomme F. Ainsi la force d'attraction F est proportionnelle à la masse de M.
L'attraction F d'un objet de masse m quelconque est donc égale à F = m.a, en désignant par a la force de gravitatation exercée sur un objet de masse 1kg. Si M n'est soumis à aucune autre force, par la deuxième loi de Newton, il subit une accélération égale à F / m = (m.a)/m = a.
En résumé, par sa seule présence, le corps S modifie l'espace environnant: En chaque point A il existe un vecteur a qui est l'accélération commune à tous les objets placés en A, libres de toute autre force que la force d'attraction de S. Ce vecteur est appellé la valeur au point A du champ gravitationnel de S.
Sur la figure le point A est extérieur à S. Mais le calcul est exactement le même s'il est à l'intérieur. L'attraction en un point intérieur est en général plus faible car les cubes élémentaires se répartissent dans toutes les directions autour de M et leurs attractions s'opposent les unes aux autres.
Le champ gravitationnel de S est ainsi bien défini; mais son calcul effectif par la méthode présentée ici suppose connue la distribution des masses à l'intérieur de S. Ce n'est en général pas le cas, en particulier lorsque S est la Terre.