Il n'y a pas plus de 5 types de polyèdres réguliers
Un sous-ensemble p du plan est convexe s'il satisfait la propriété suivante: si p contient les point P et Q il contient tous les points du segment PQ.
Les angles auxquels on s’intéresse ici sont uniquement des angles non orientés de demi-droites, dont la mesure est un nombre compris entre 0 et 180°
La somme des angles d'un polygone convexe à n côtés est (n-2) × 180°.
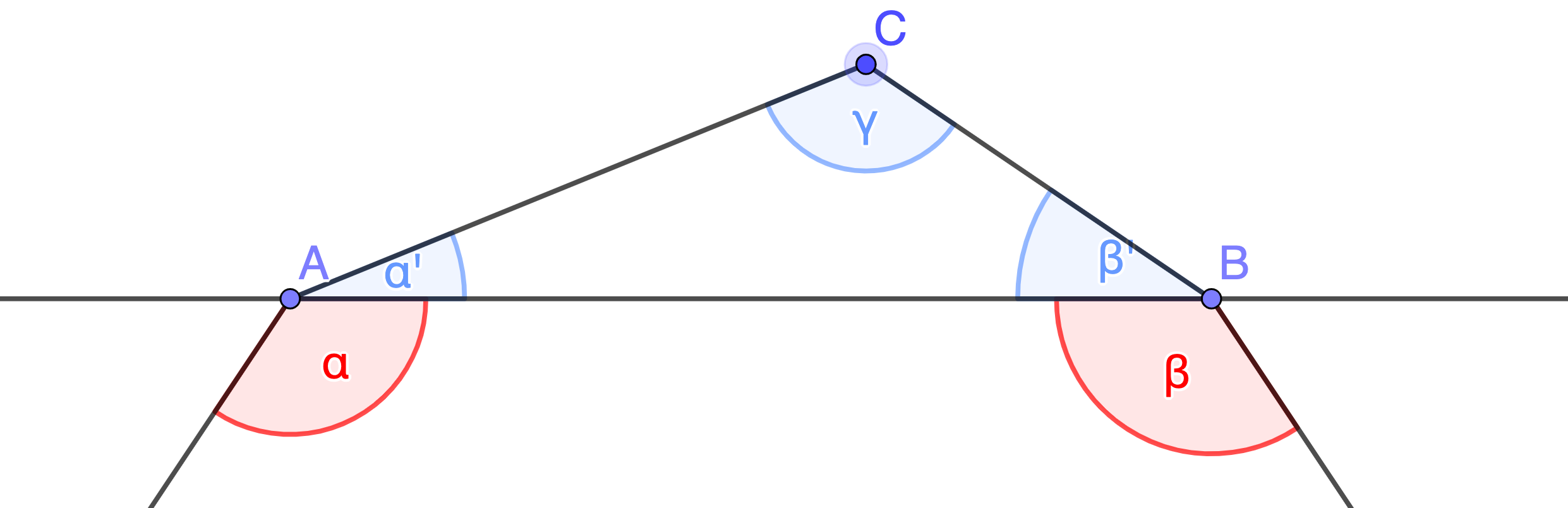
Soit P un polygone convexe à n côtés. Si n=3, P est un triangle et la somme de ses angles est 180° = (3-2) × 180°. Il suffit de démontrer que l'ajout d'un nouveau sommet à P augmente la somme de ses angles de 180°. Soit C le nouveau sommet ajouté entre A et B. Pour que le polygone reste convexe après l'ajout de C il faut que C et P soient de part et d'autre de la droite AB. Avant cet ajout l'angle en A (resp. B) était α (resp. β). Après l'ajout l'angle en A (resp. B) devient α + α' (resp. β + β'). Avec le nouvel angle γ qui vient s'ajouter en C la somme des angles est augmentée de α' + β' + γ = 180° car ces trois angles sont les trois angles du triangle ABC.
Un trièdre est la figure définie par trois demi-droites non coplanaires ayant un unique point commun S, le sommet du trièdre.
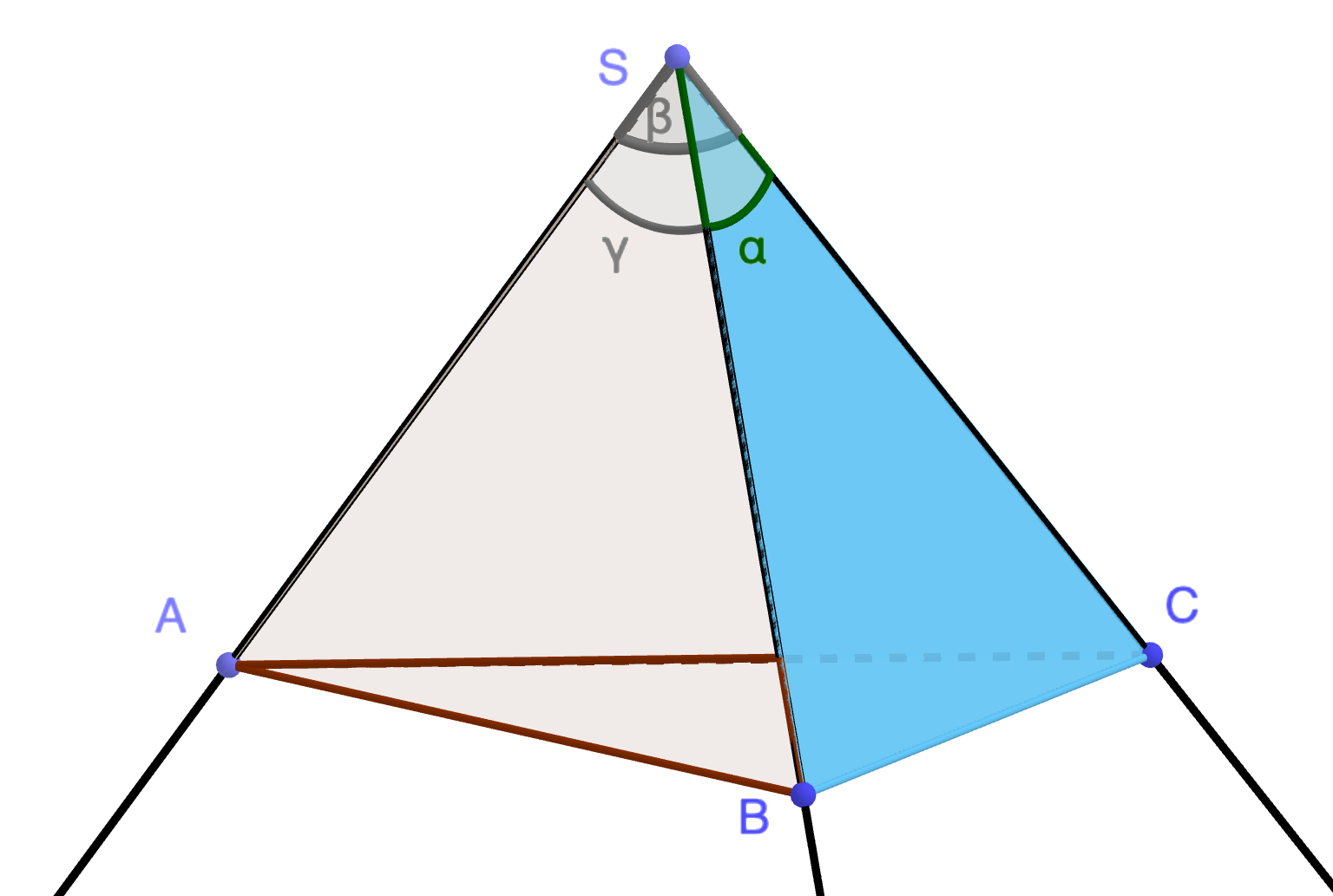
Chacun des 3 angles en un même sommet d'un trièdre est inférieur à la somme des 2 autres.
Cette inégalité est assez naturelle. Soit un plan π qui rencontre les trois arêtes du trièdre en trois points A,B,C. L'inégalité triangulaire classique dit que dans le triangle ABC la longueur de chacun des côtés est inférieure à la somme des longueurs des deux autres côtés. Les trois angles α, β, γ au sommet S du tétraèdre SABC, sont les angles sous-lequels on voit les trois côtés BC, CA et AB. Il est donc raisonnable de s'attendre à ce qu'aucun de ces trois angles ne soit supérieur à la somme des deux autres. Nous admettrons cette propriété pour ne pas pas alourdir encore ce texte (Démonstration ici, fichier pdf triedre.pdf)
Un polyèdre convexe est une partie convexe de l'espace dont la frontière est une réunion finie de polygones qu'on appelle ses faces. Deux faces ne sont jamais contenues dans un même plan. L'intersection de deux faces qui ne sont pas disjointes est appelée une arête.
Une pyramide est un polyèdre P défini par un polygone, appelé la base de P et un point S appelé le sommet de P. Les faces de P sont le polygone de base et les faces latérales. A chaque côté AB de la base est associé une face latérale, le triangle SAB.
La proposition suivante dit que la somme des angles au sommet d'une pyramide est toujours plus petite que 360°. Ce résultat peut sembler évident à beaucoup, d'autant plus qu'il est très facile à démontrer dans le cas particulier où la projection orthogonale du sommet S est à l'intérieur de la base. La démonstration dans le cas général est un peu plus délicate et s'appuie sur la Proposition 2.
La somme des angles au sommet d'une pyramide convexe est plus petite que 360°.
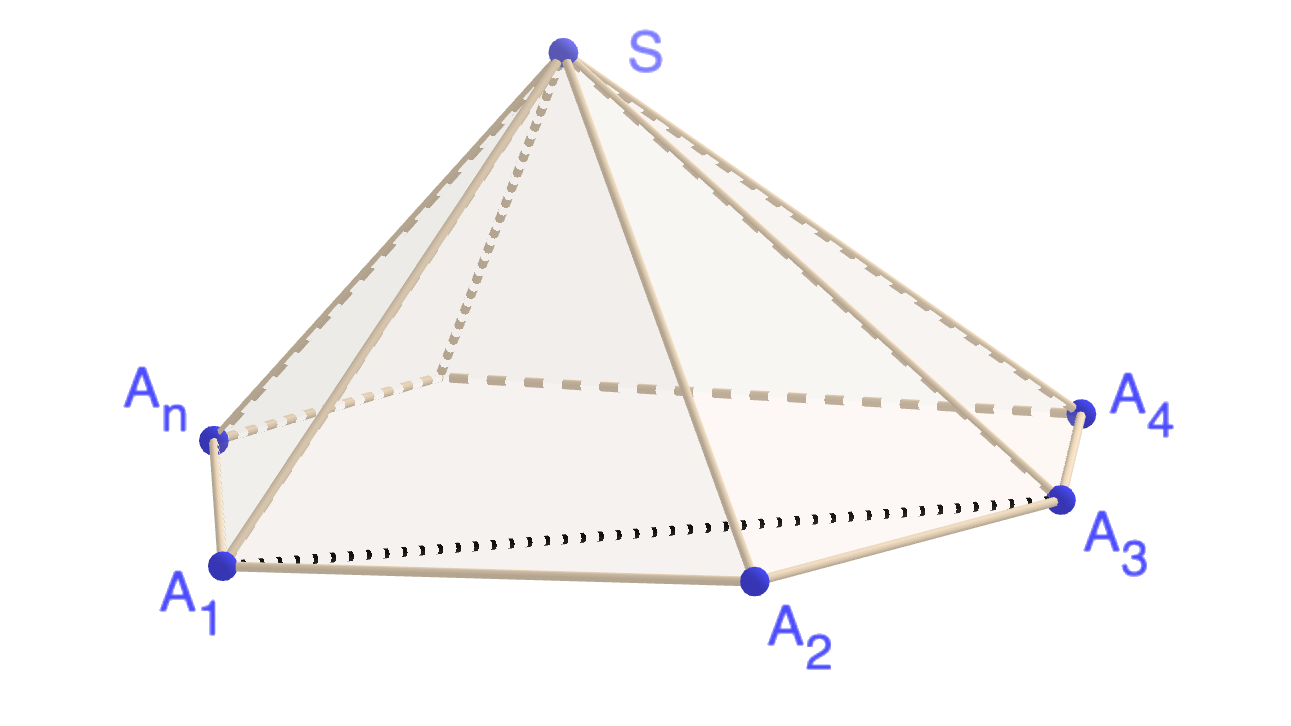
Notons σ la somme des angles au sommet de la pyramide. L'inégalité triangulaire au sommet d'un trièdre appliquée aux trièdres de sommets A2, A3, A4, … A1 donne les inégalités
En ajoutant membre à membre toutes ces inégalités on obtient à gauche la somme des angles du polygone de base c'est à dire (n-2) × 180 et à droite la somme
qui s'écrit encore, en modifiant l'ordre des termes
Chacune des termes entre crochets est la somme des deux angles à la base de l'une des faces latérales. Chaque crochet est donc le supplémentaire de l'un des angles au sommets de la pyramide. Cette somme est donc égale à n × 180 - σ. On a donc
c'est à dire σ < 360.
Un polyèdre régulier est un polyèdre convexe dont chaque sommet est entouré d'un même nombre de
faces, q, qui sont toutes identiques à un même polygone régulier à p côtés. Le couple (p,q)
est appelé le type de ce polyèdre.
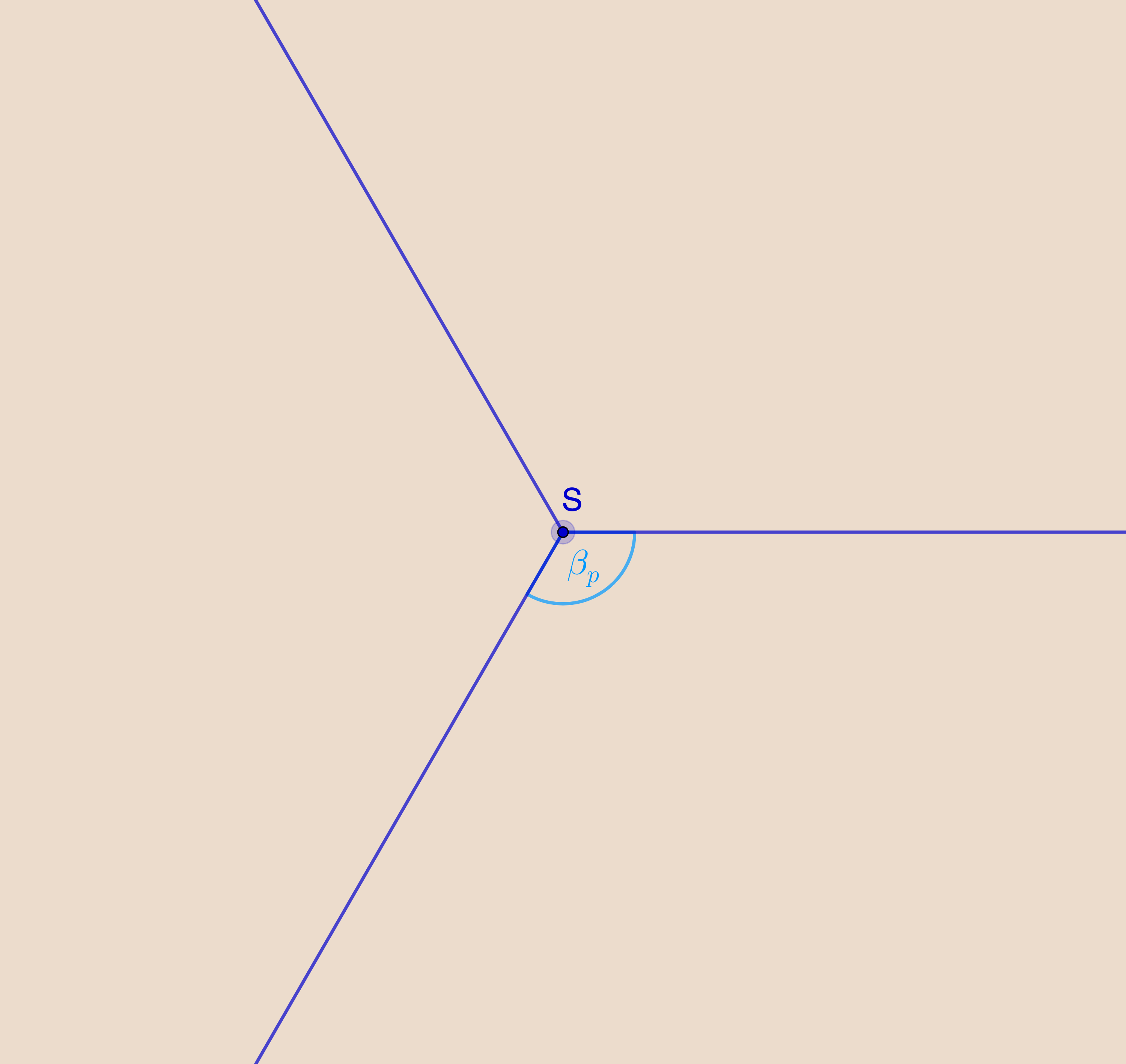
La figure ci-contre montre le voisinage d'un sommet d'un polyèdre de type (p,3). Chaque sommet est entouré de 3 polygnes réguliers à p côtés.
Que peut-on dire de p et q? Puisque chaque sommet est un coin, il est entouré d'au moins trois faces. Donc p ≥ 3.
Puisque les faces sont des polygones à p côtés les angles au sommet sont tous égaux à βp = (p-2)/p × 180°, par la proposition 1. Puisqu'il y a q faces autour de chaque sommet la somme des angles au sommet est qβp. Cette somme est plus petite que 360° par la proposition 3, ce qui donne q < 360 / βp. Ainsi, pour chaque valeur de p les seules valeurs possibles de q sont les entiers saisaisant 3 ≤ q < 360 / βp
Il existe au plus 5 types de polygones réguliers, les types (3,3), (3,4), (3,5), (4,3), (5,3)
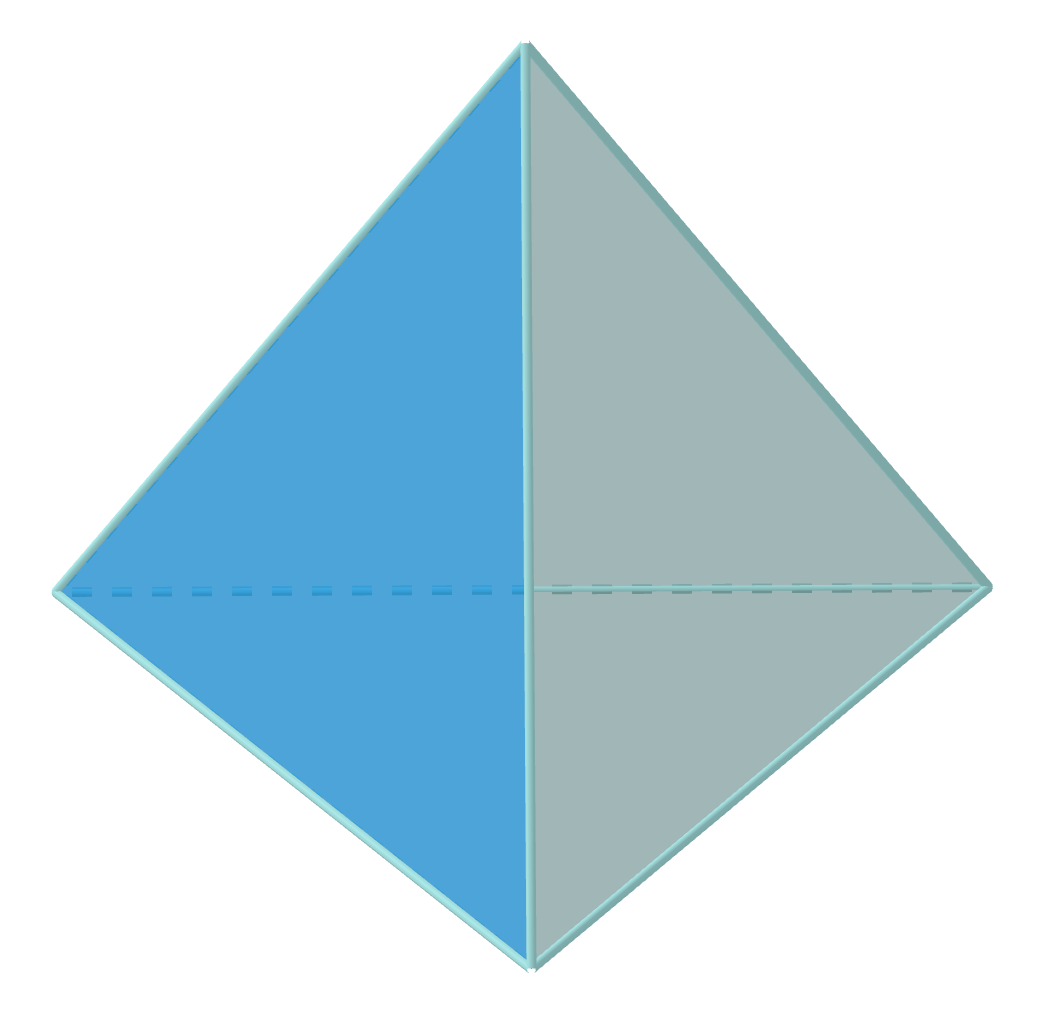
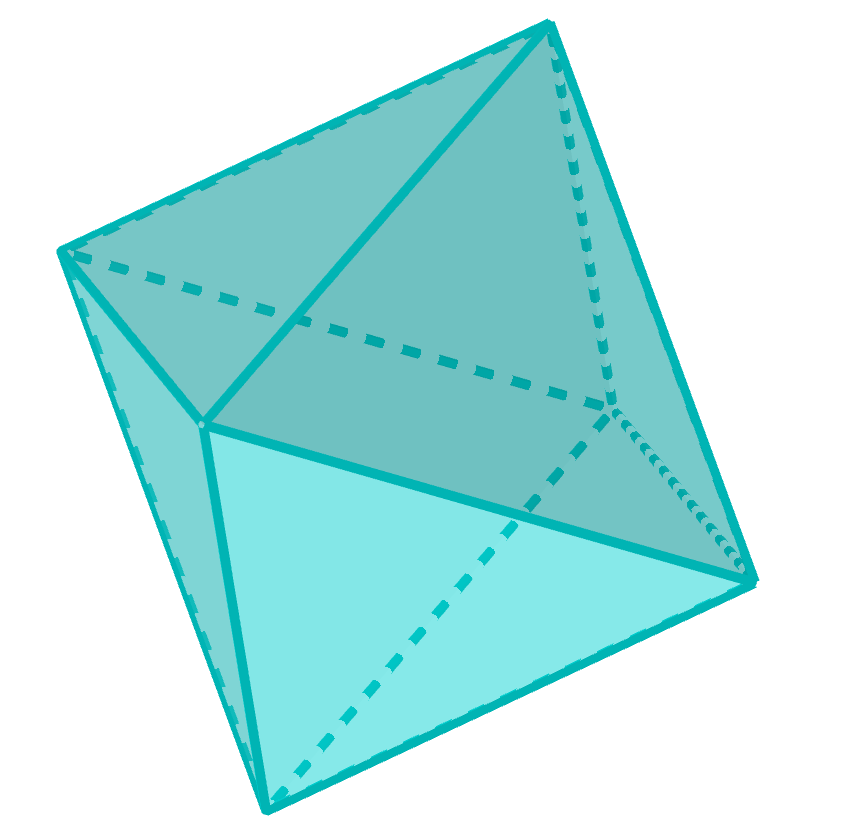
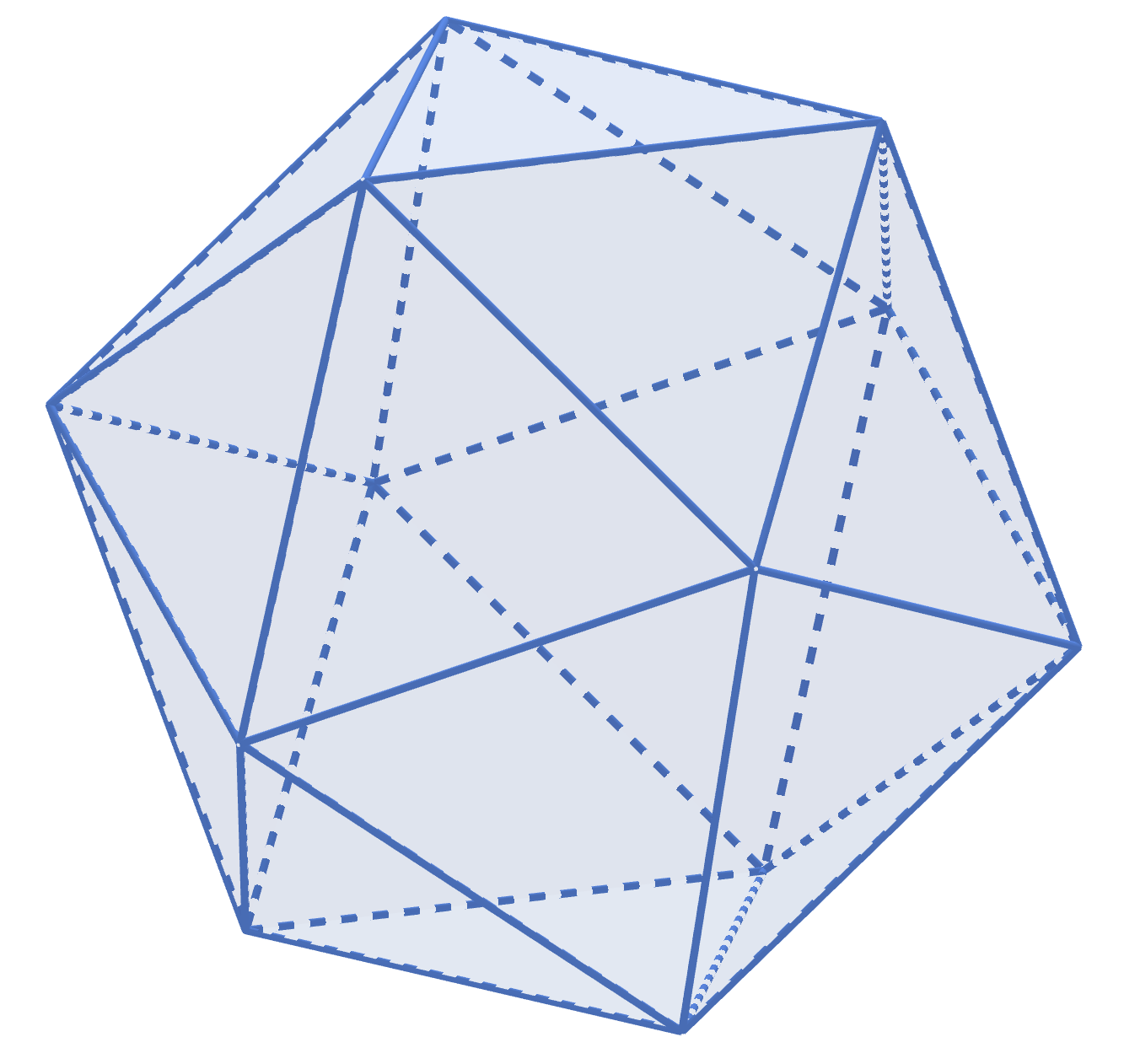
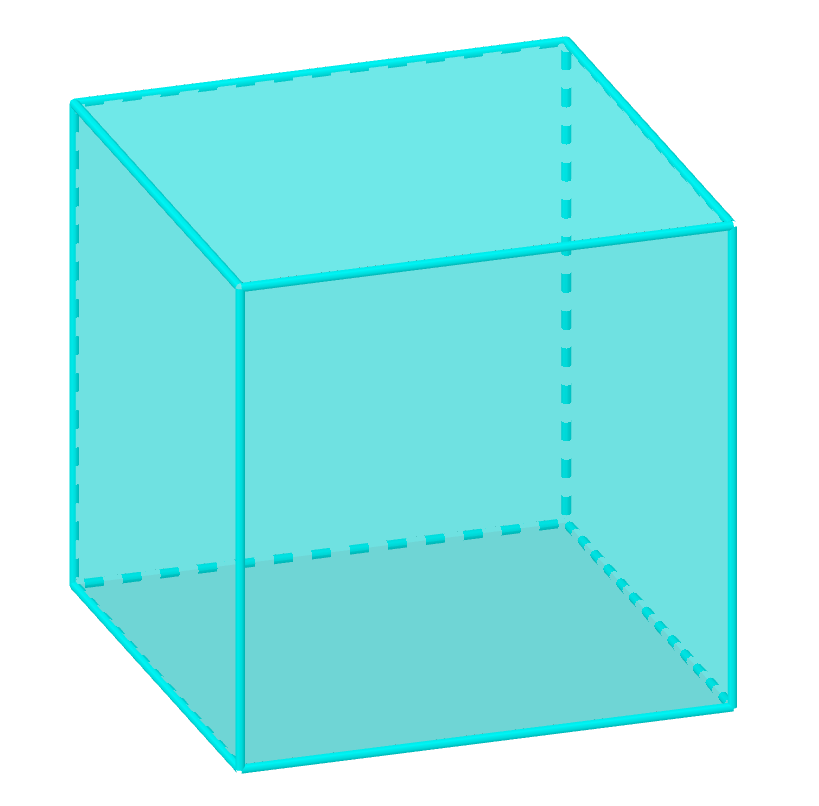
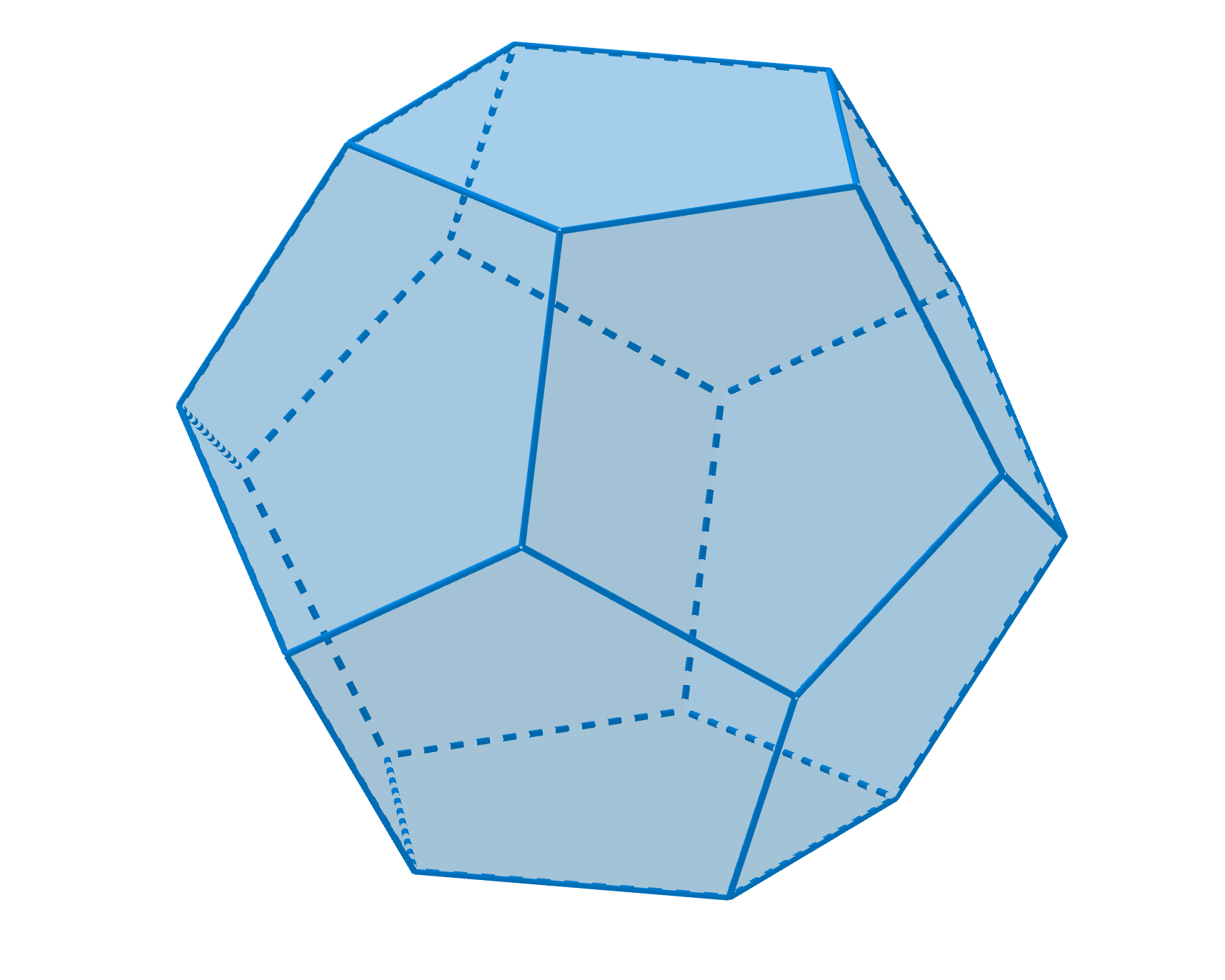
Soit P un polyèdre régulier de type (p,q). Le nombre S de ses sommets et le nombre F de ses faces s'obtiennent très simplements à l'aide du nombre A de ses arêtes.
Les nombres de sommets et de faces d'un polyèdre régulier de type (p,q) avec A arêtes sont donnés par S = 2A/q, F = 2A/p.
Outre les équations de la proposition 5, une troisième égalité nous est fournie par une importante équation reliant les nombres de sommets, d'arêtes et de faces d'un polyèdre convexe quelconque, démontrée par Euler en 1748.
Les nombre de sommets S, nombre d'arête A et nombre de face F d'un polyèdre convexe satisfont l'équation S - A + F = 2
Par exemple, dans le cas du cube, 8 sommets, 12 arêtes et 6 faces, on a bien 8 - 12 + 6 = 2.
Les nombres de sommets, d'arêtes et de faces d'un polyèdre régulier de type (p,q) sont donnés par
| S = 4p 2p + 2q - pq | A = 2pq 2p + 2q - pq | F = 4q 2p + 2q - pq |
En remplaçant S et F dans l'équation d'Euler S - F + A = 2 par 2A/q et 2A/p (cf Proposition 5) on obtient 2A/q - A + 2A /p = 2, qui donne la valeur de A = 2pq/(2p + 2q - pq). En utilisant à nouveau la Proposition 5 on en déduit les valeus de S et F.
En utilisant ces formules on dresse le tableau suivant:
| Nom | type = (p,q) | Sommets | Arêtes | Faces |
| Tétraèdre | (3,3) | 4 | 6 | 4 |
| Hexaèdre | (4,3) | 8 | 12 | 6 |
| Octaèdre | (3,4) | 6 | 12 | 8 |
| Dodécaèdre | (5,3) | 20 | 30 | 12 |
| Icosaèdre | (3,5) | 12 | 30 | 20 |