L’utilisation d’un logiciel facilite la classification des triangles et des quadrilatères. Le carré apparaît plus naturellement comme cas particulier de rectangle quand on peut faire varier continûment les dimensions d’un rectangle.
Ainsi, la situation du triangle BON propose une famille de triangles isocèles, et l’on attend des élèves qu’ils comprennent comment ils ont été « construits pour être isocèles ». Certains cependant, en début de cinquième, notent que le triangle peut être isocèle ou équilatéral. Outre le recours habituel à la définition ( un triangle isocèle est un triangle qui a au moins 2 côtés égaux), on peut s’appuyer ici sur ce qui varie : l’angle au sommet, et remarquer que cet angle détermine les différentes formes de triangles isocèles, avant de conclure que le triangle peut être isocèle et équilatéral, mais est dans tous les cas isocèle.
L'apport du logiciel est évident dans la classification des triangles et des quadrilatères. Mais un triangle équilatéral a beau être isocèle, quand l’énoncé demande un triangle isocèle, il est généralement mal choisi de le tracer équilatéral ! Les élèves doivent aussi comprendre l'intérêt d’éviter les cas particuliers pour raisonner.
Voici un exemple. On a demandé aux élèves de tracer sur le cahier deux cercles concentriques et un diamètre de chaque cercle. Beaucoup d'entre eux tracent spontanément deux diamètres perpendiculaires, et en déduisent que cette construction produit un losange.
| L'enseignant reproduit leur figure avec cabri, en plaçant à vue les deux diamètres perpendiculaires. et le déplacement d'un point montre immédiatement en quoi elle est trompeuse. Des élèves peuvent alors suggérer de regarder ce qui se passe si l'on change la taille des cercles, si les deux cercles sont confondus... |
La notion de « figure quelconque » n’est pas si simple, une figure n'est particulière que par rapport au problème étudié, si elle porte des propriétés supplémentaires pouvant parasiter le raisonnement dans ce problème, comme on le voit dans l’exemple suivant .
Soit l'énoncé suivant.
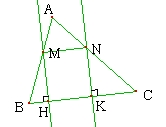
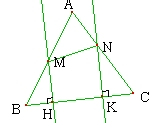
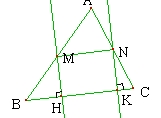
Tracer un triangle quelconque ABC. Placer un point M sur [AB] et un point N sur [AC]. La perpendiculaire à (BC) passant par M coupe [BC] en H et la perpendiculaire à (BC) passant par N coupe [BC] en K. Quelle est la nature du quadrilatère MNKH ?


