The shape of a theorem

Leonard Hardiman

Introduction

  • Ingredients for a mathematical anecdote:
    • accessibility
    • wow-factor
    • honesty.

  • Principle: the best way to know a (mathematical) object is to know where it lives, to understand its landscape.

  • We examine the question, “where do theorems live?” via a single case study: Pappus’ theorem.

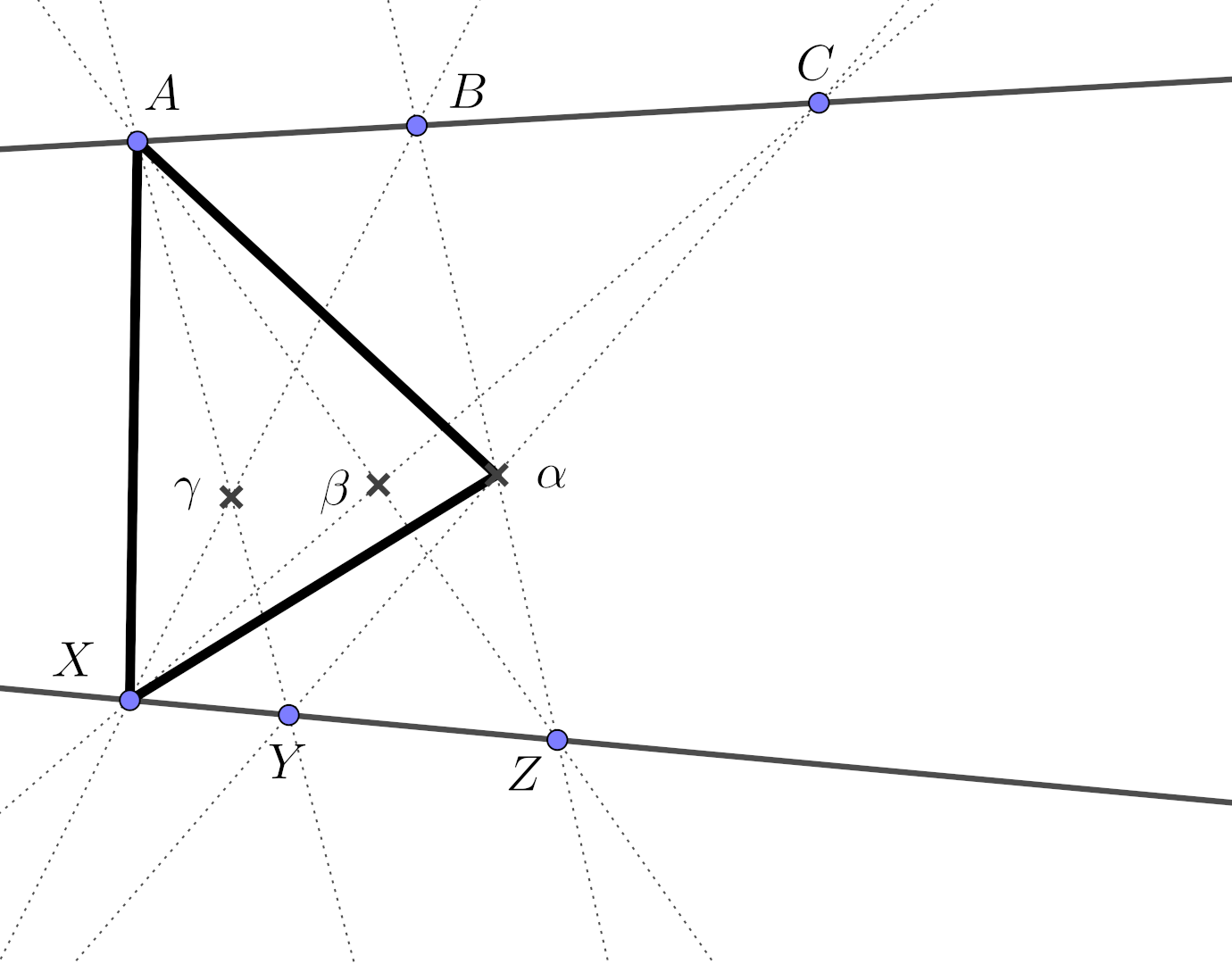
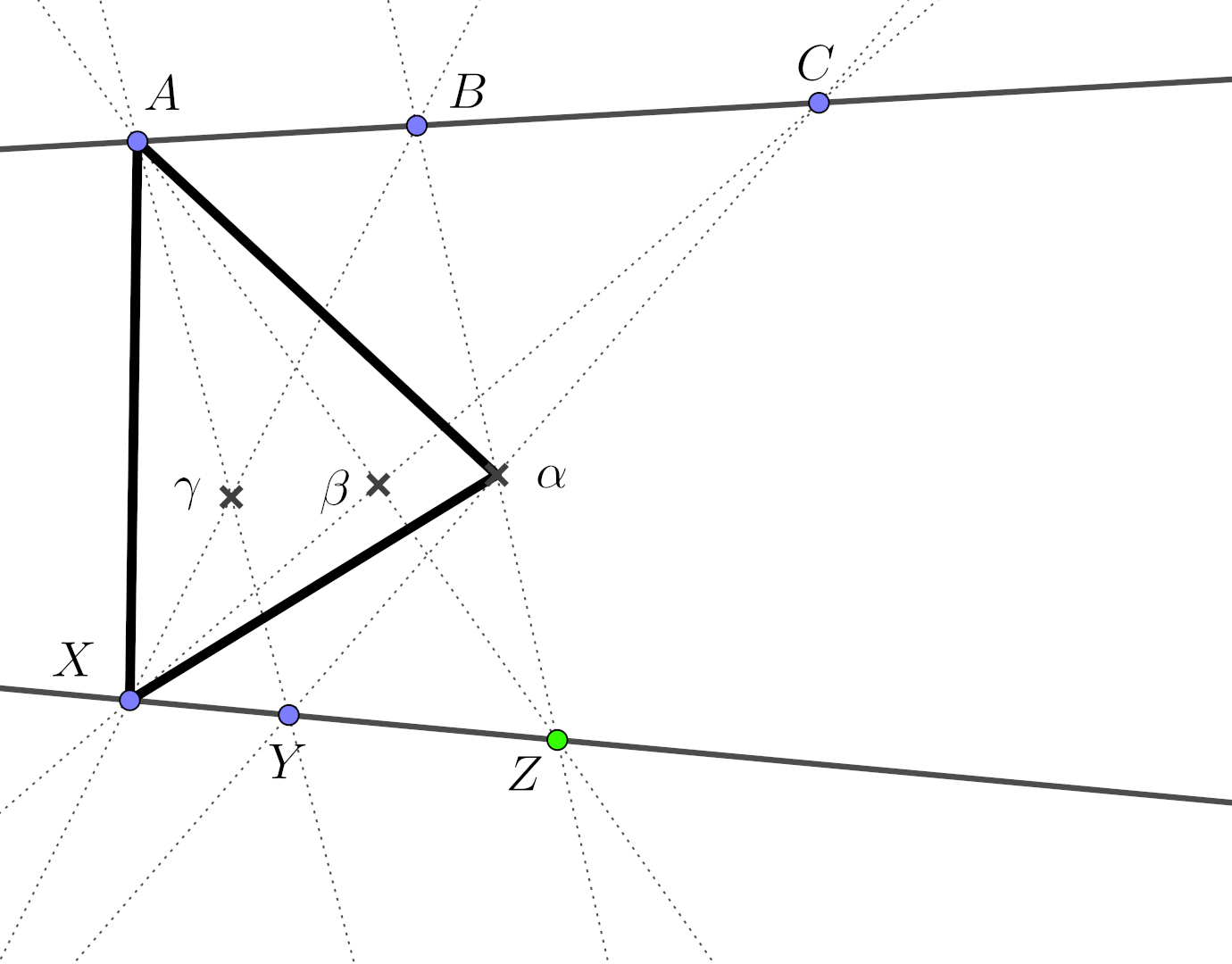
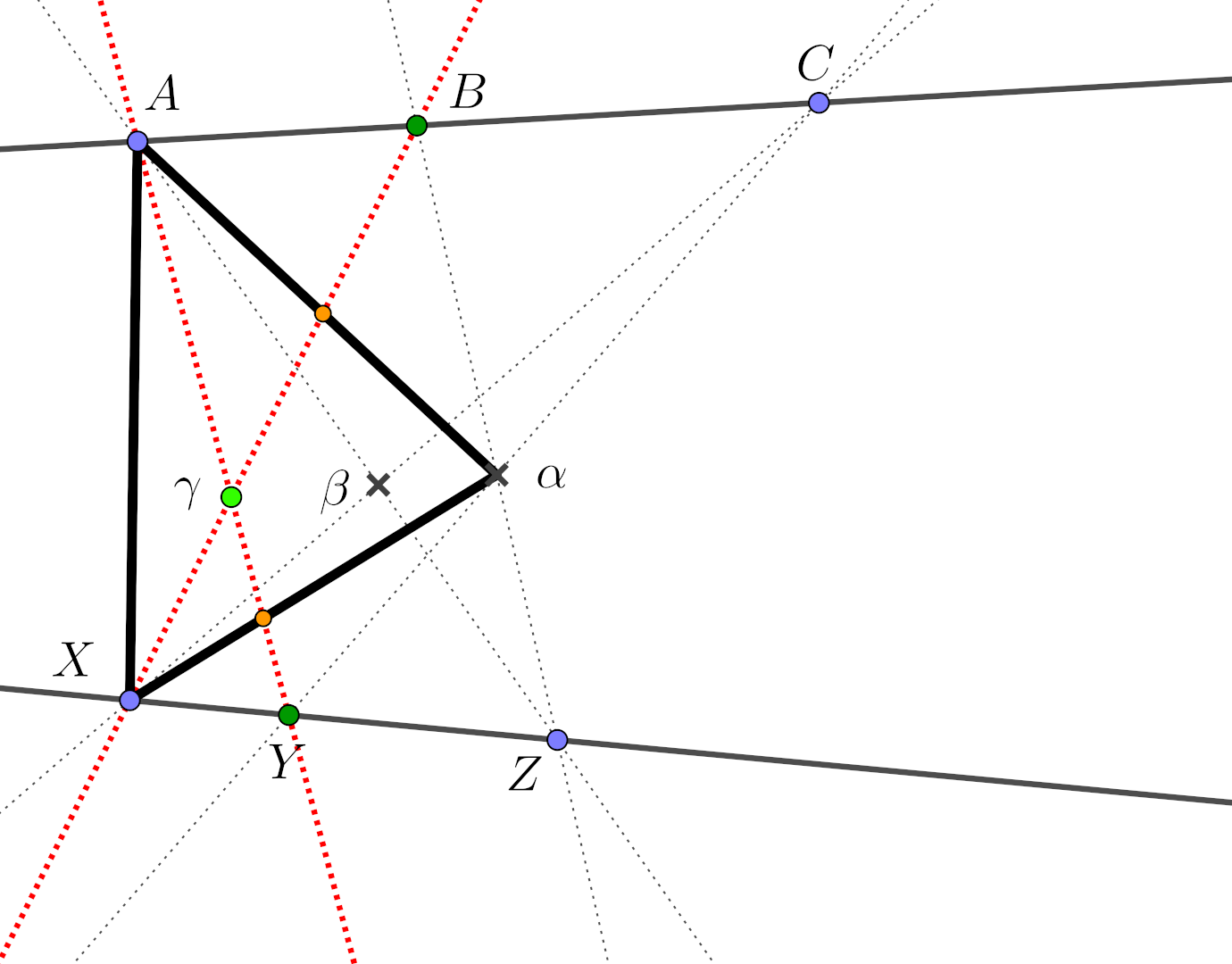
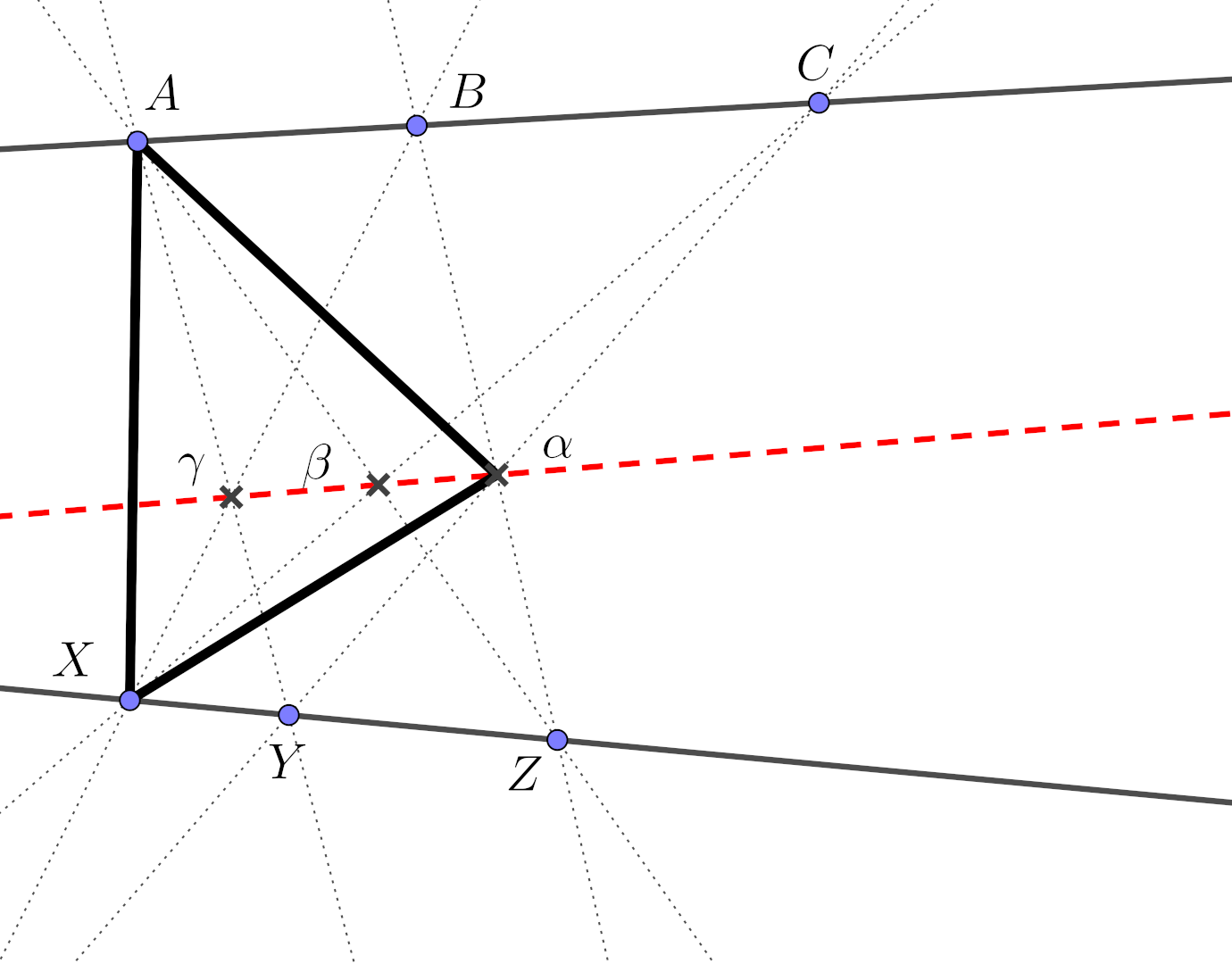
Pappus’ theorem

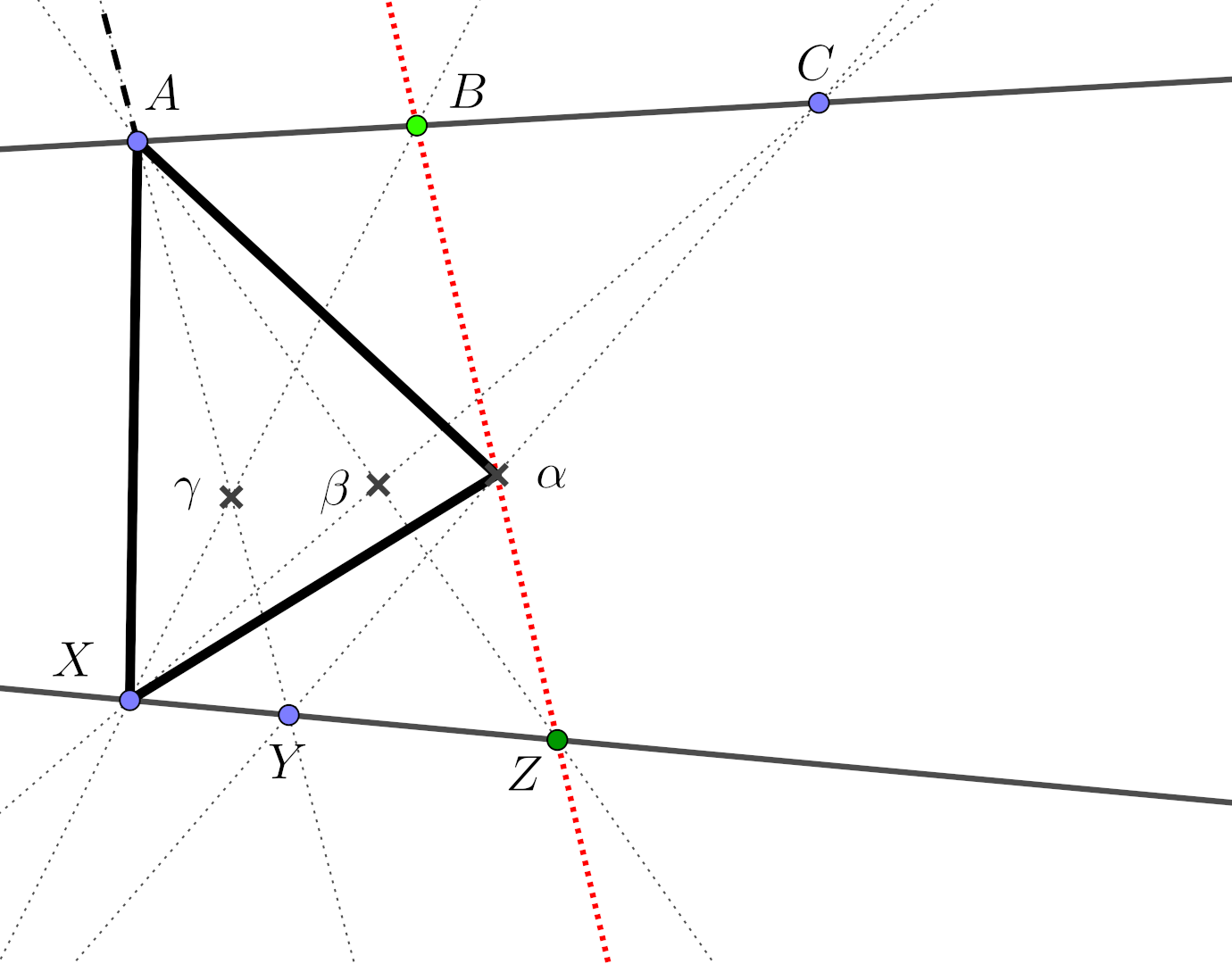
Let \(\{A,B,C\}\) and \(\{X,Y,Z\}\) be two distinct triples of collinear points. Then the points \(\gamma = (A,Y) \cap (B,X)\), \(\beta = (A,Z) \cap (C,X)\) and \(\alpha = (B,Z) \cap (C,Y)\) are also collinear.

Plan :

  • Ceva’s theorem

  • Topological proof
    (the shape is revealed)

  • An algorithm

  • Conclusion

Ceva’s theorem

Let \(ABC\) be an oriented triangle and let \(D\) be a point. We consider \(X,Y,Z\) as in the figure below. Then, the signed lengths of segments satisfy,

\[\begin{align*} \frac{|AX|}{|XB|} \cdot \frac{|BY|}{|YC|} \cdot \frac{|CZ|}{|ZA|} = 1. \end{align*}\]

Notes :

  • Ceva’s theorem can be proved using the fact that a triangle’s area is proportional to the length of its base.

  • Ceva’s theorem can be glued to itself…

Glueing Ceva’s theorem

Glueing Ceva’s theorem on a sphere

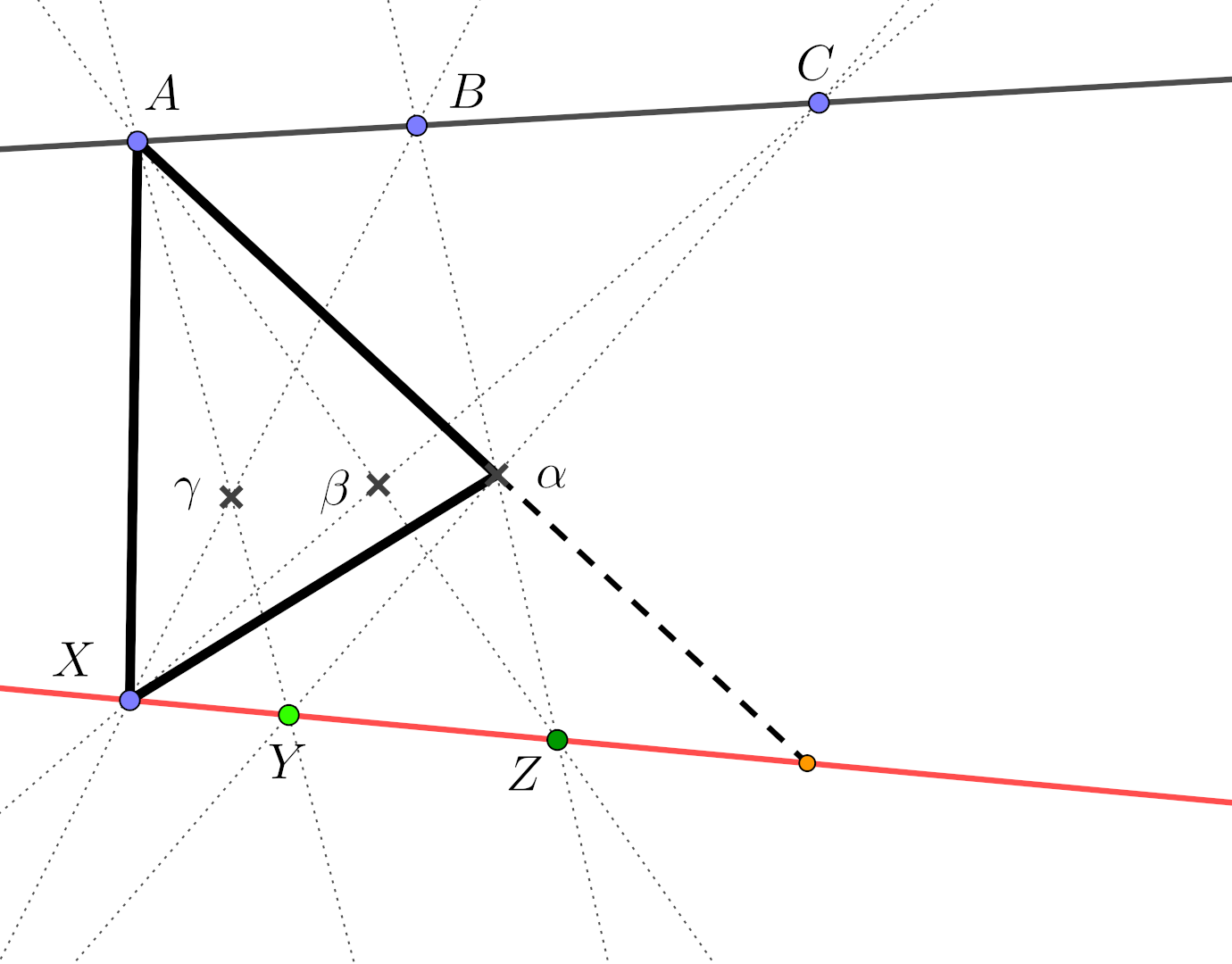
Topological proof of Pappus’ theorem

The shape is revealed

Topological proof of Pappus’ theorem

_

Topological proof of Pappus’ theorem

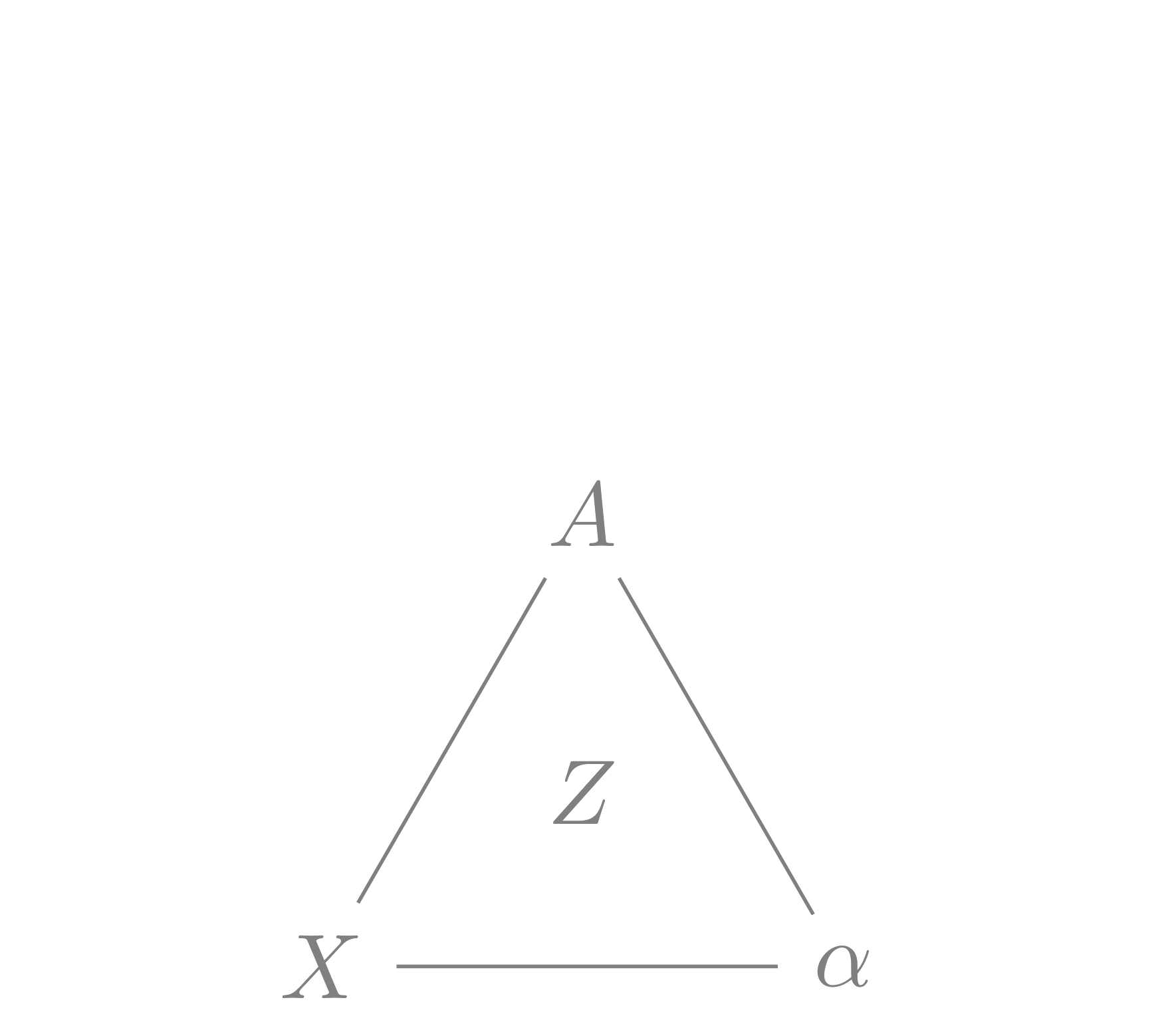
Topological proof of Pappus’ theorem

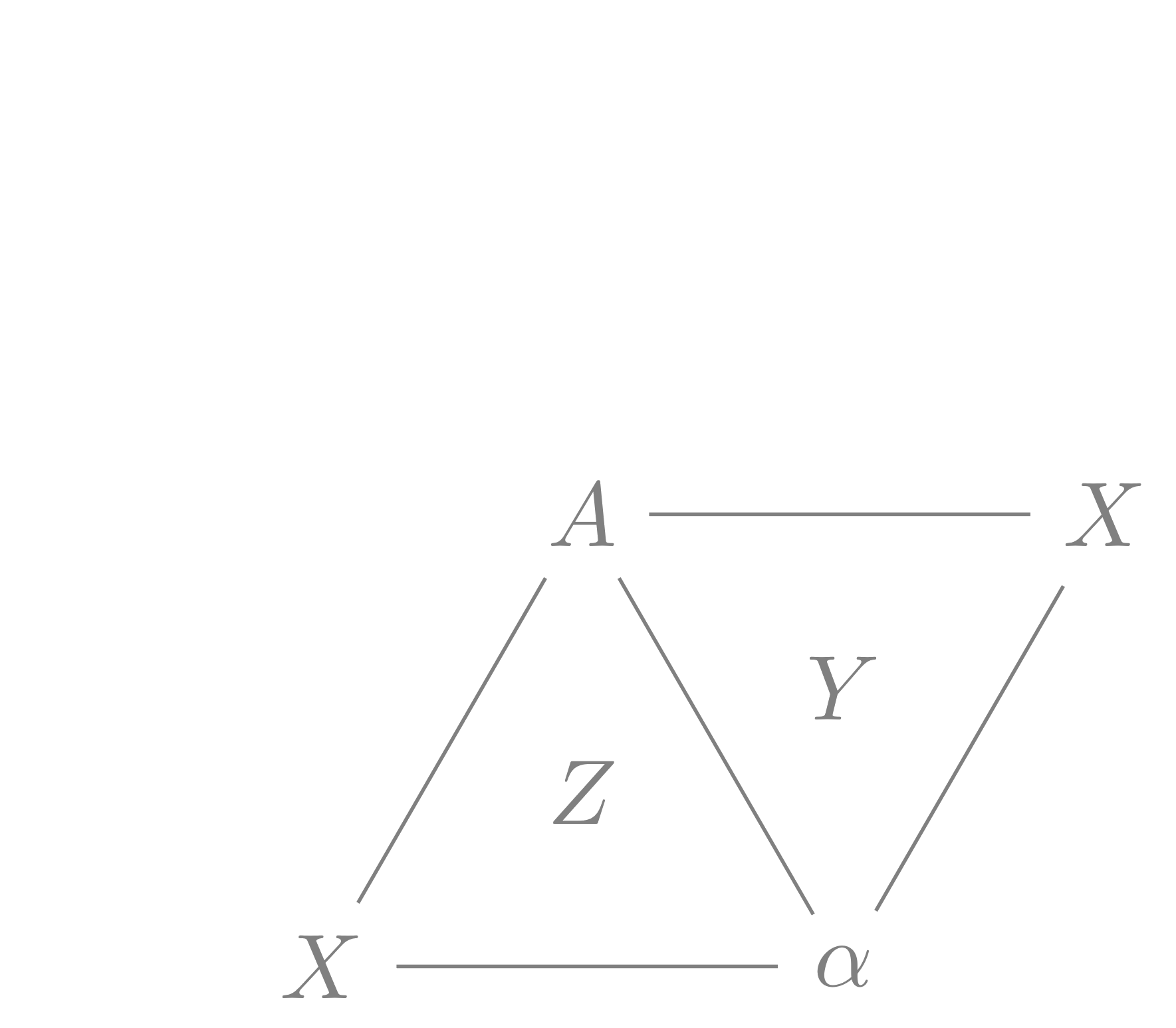
Topological proof of Pappus’ theorem

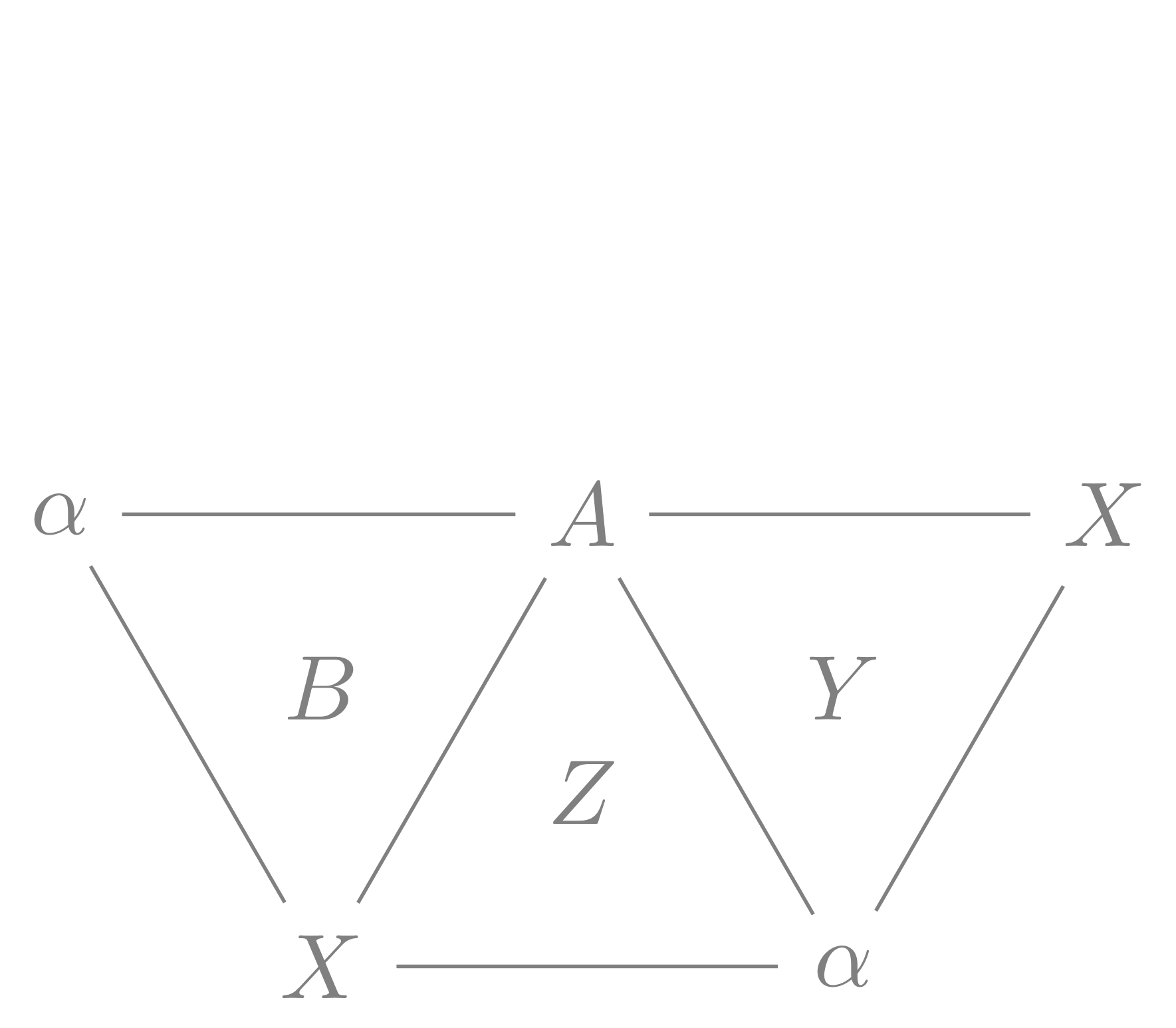
Topological proof of Pappus’ theorem

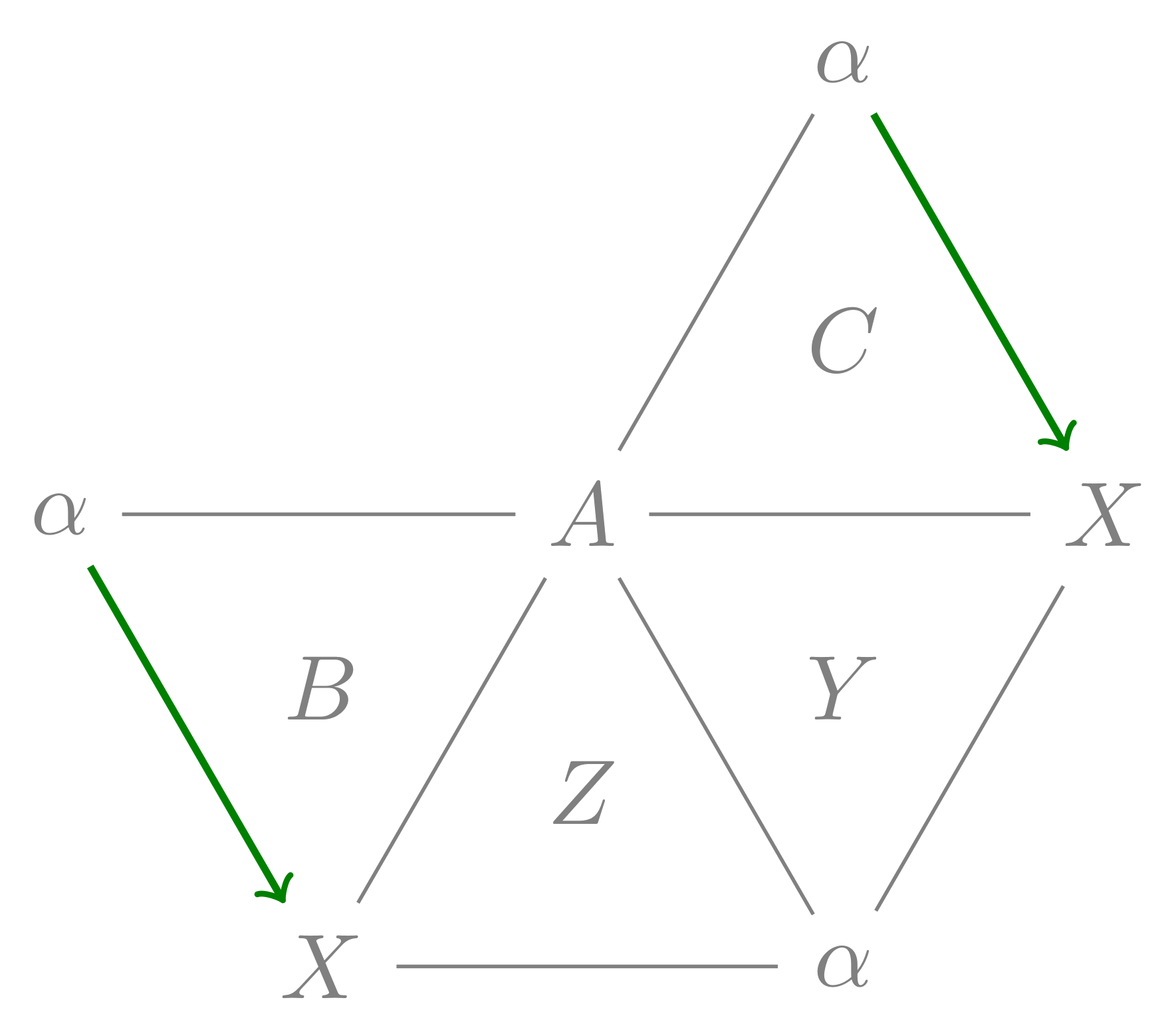
Topological proof of Pappus’ theorem

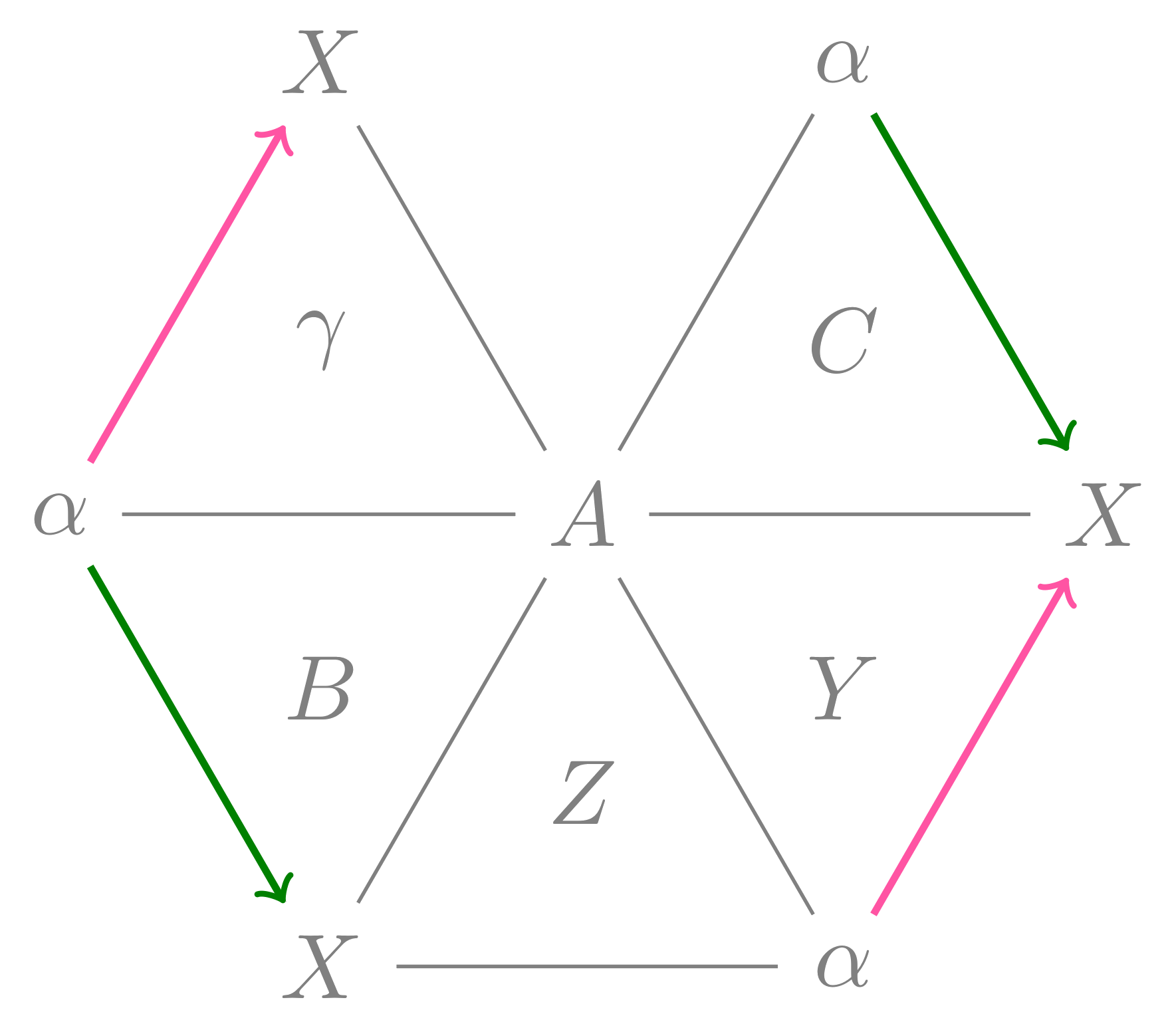
Topological proof of Pappus’ theorem

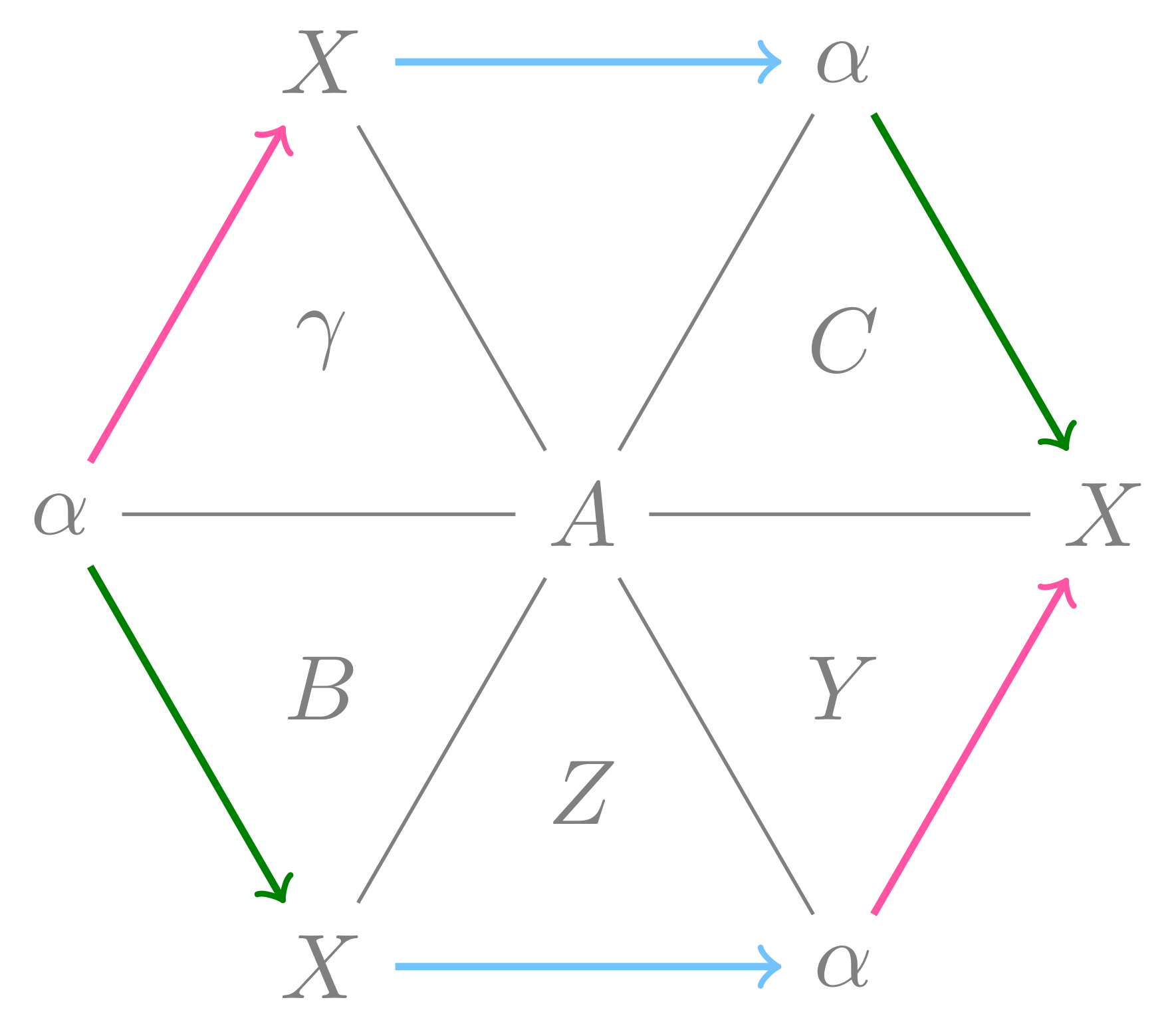
Topological proof of Pappus’ theorem

_

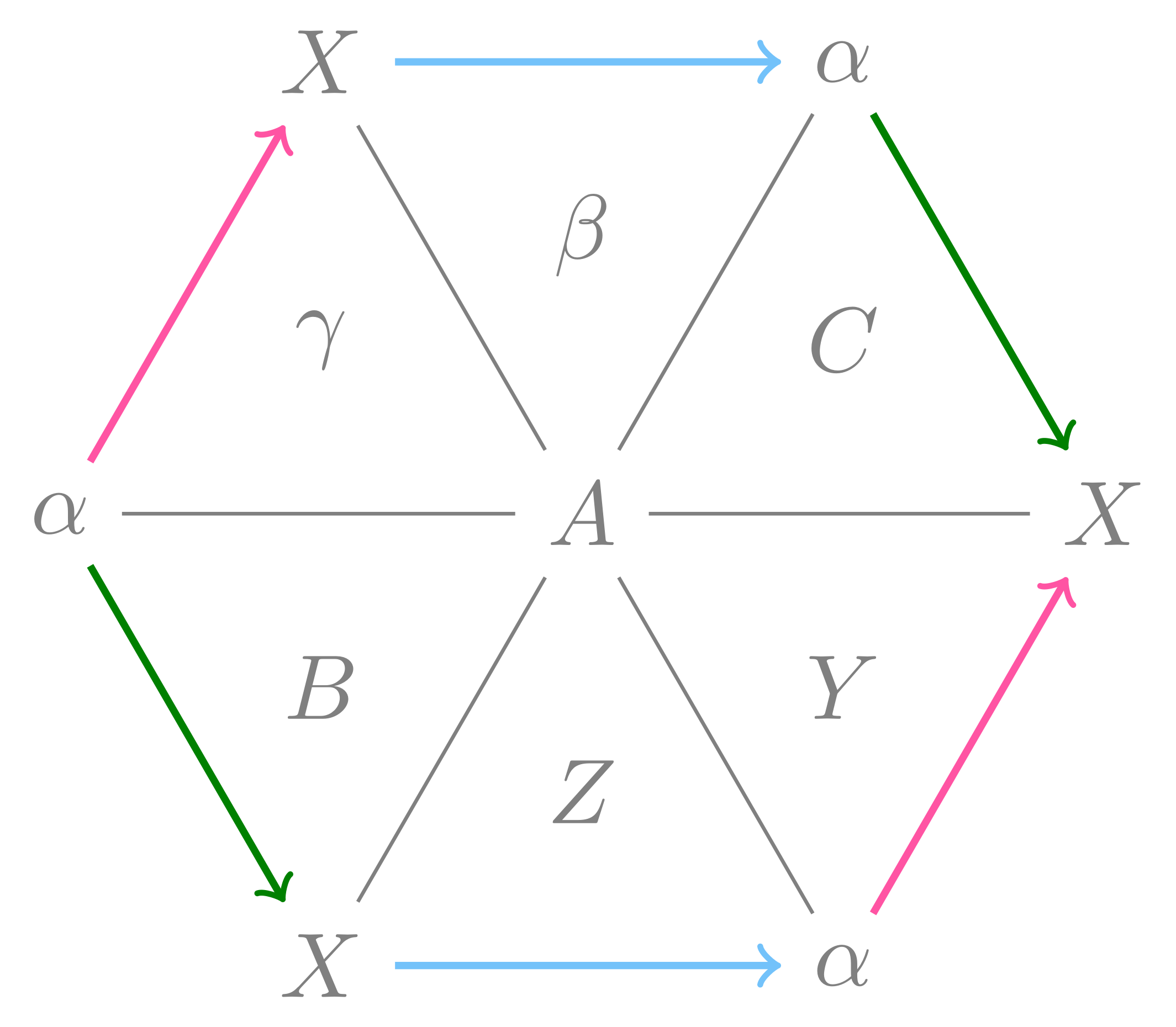
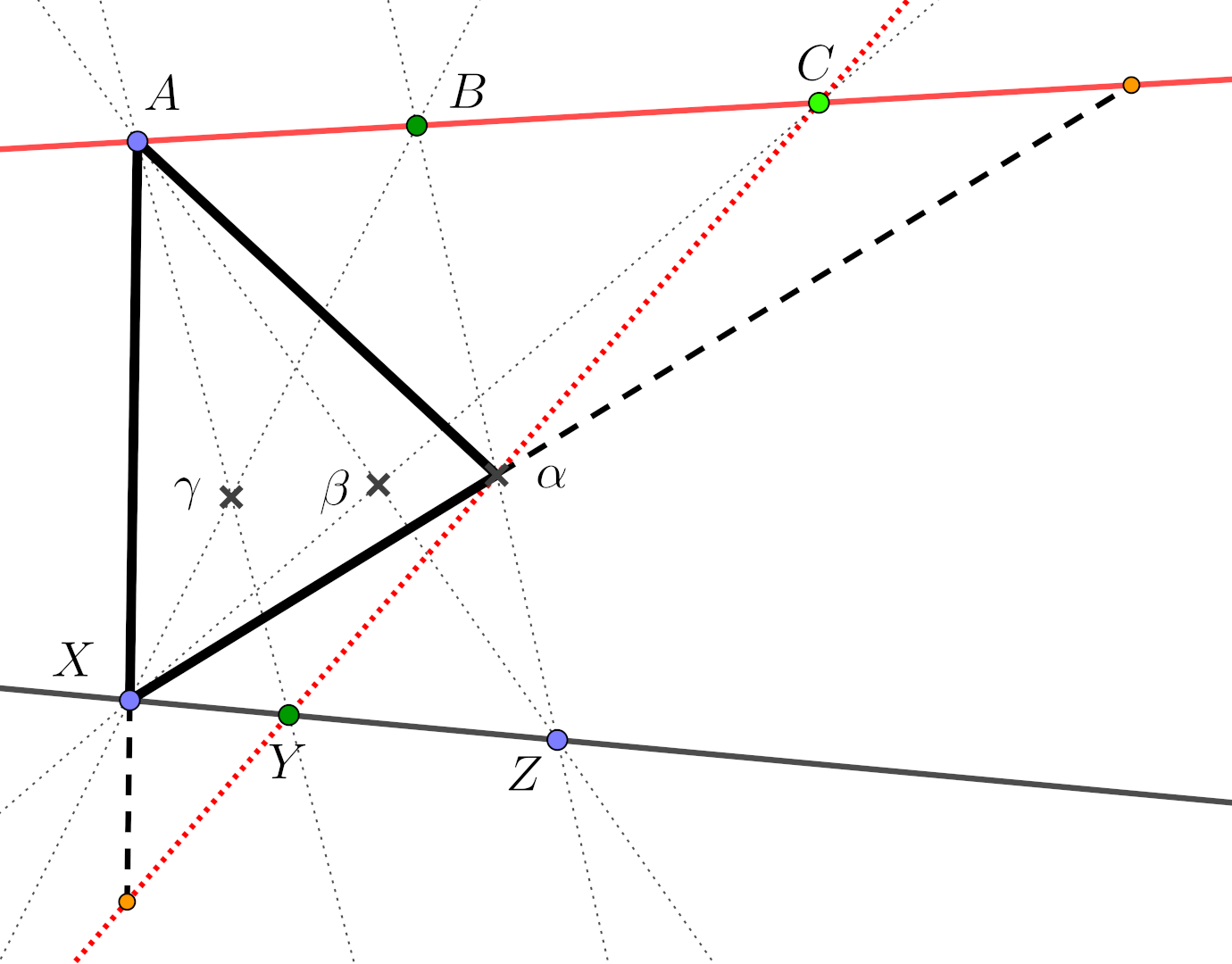
And we could have gone the other way!

Once the (triangulated) surface has been chosen, the proof just falls out!

So what is this mysterious surface?

So what is this mysterious surface?

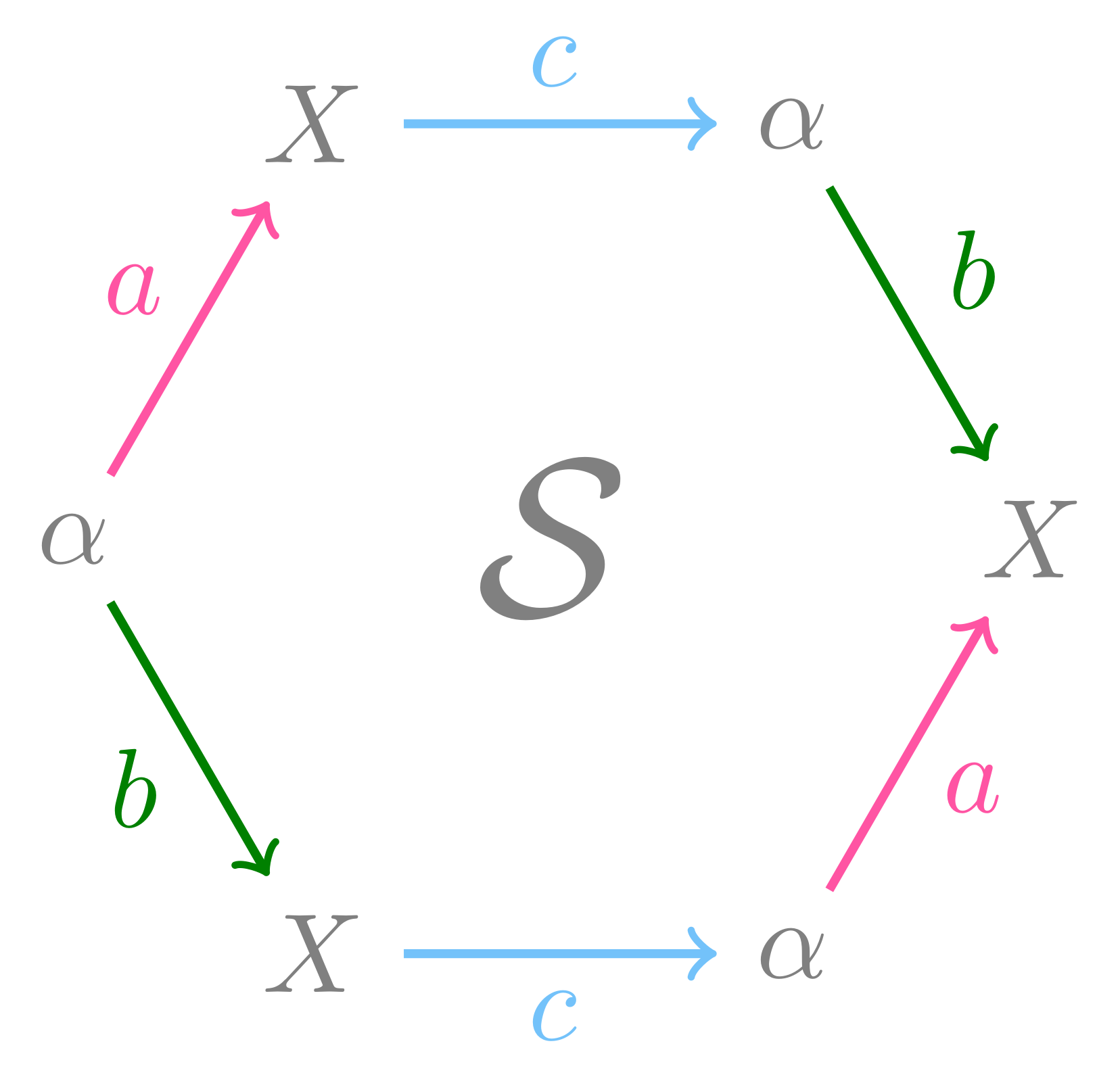
So what is this mysterious surface?

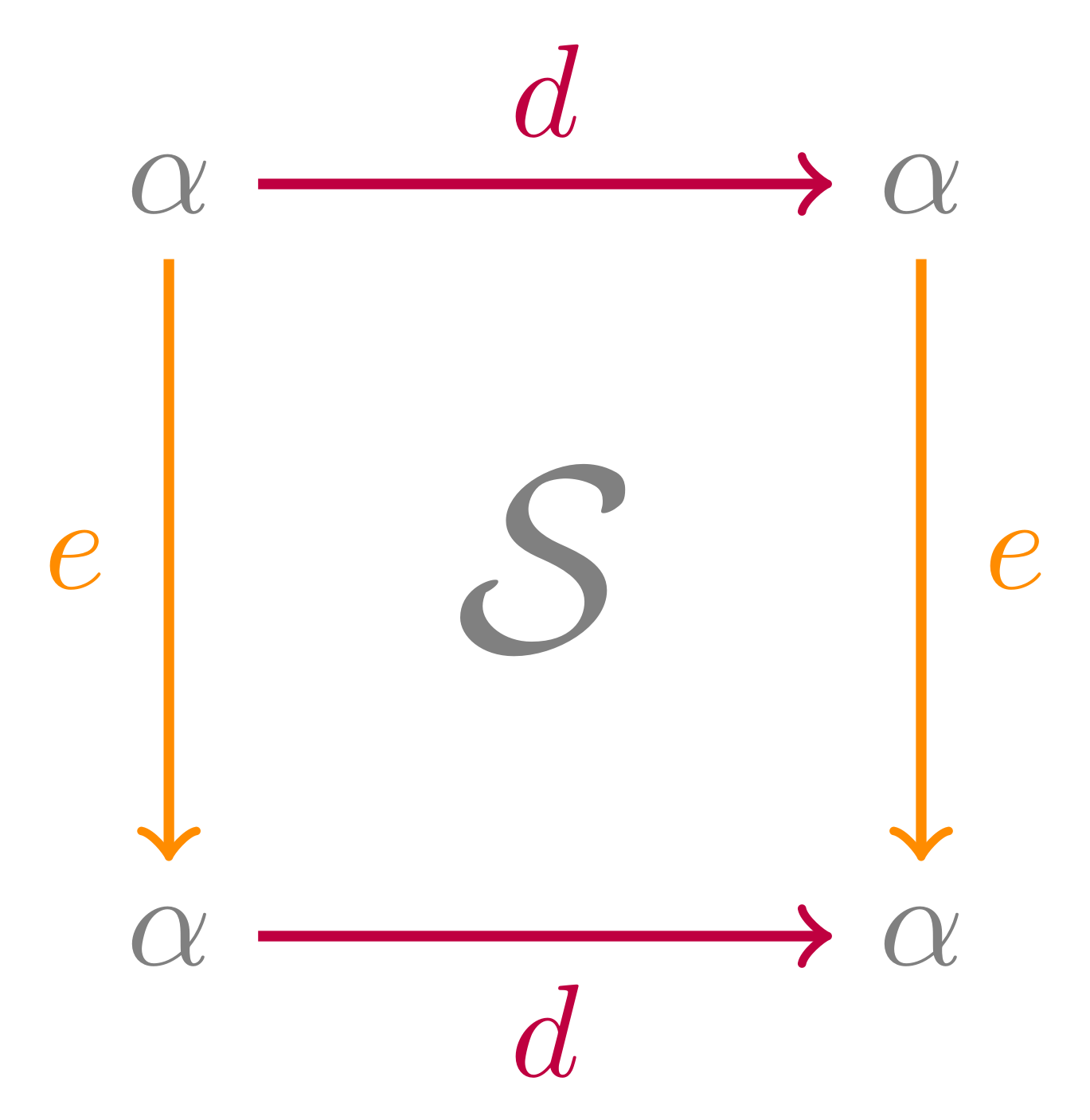
(setting \(d = a \circ c\) and \(e = b \circ a^{-1}\))

So what is this mysterious surface?

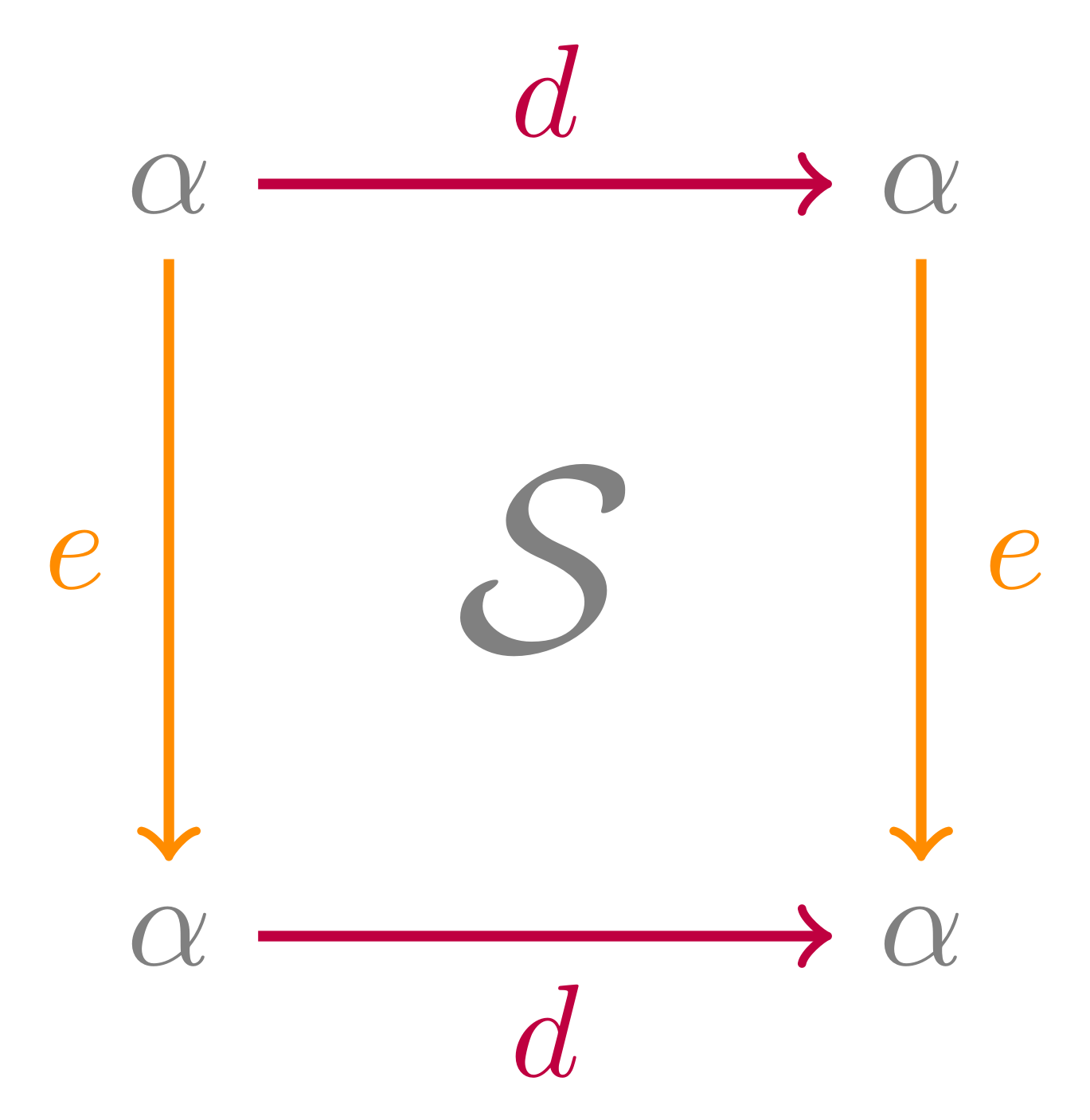
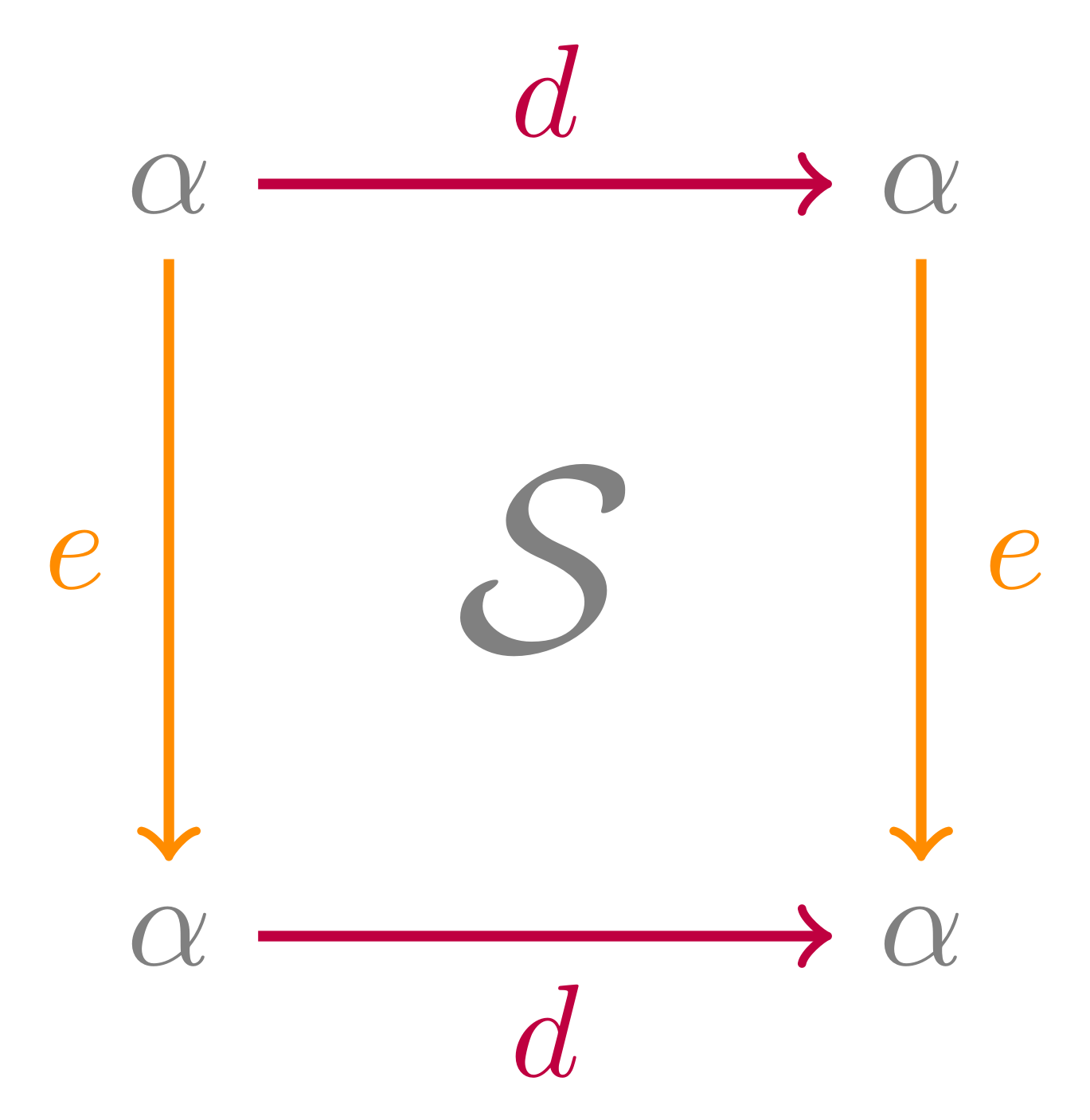
It’s a torus, the simplest non-trivial surface!

An algorithm

What would happen if we started with a different (triangulated) surface \(\mathcal{S}\)?

We would prove different theorems! This gives us a theorem finding algorithm.

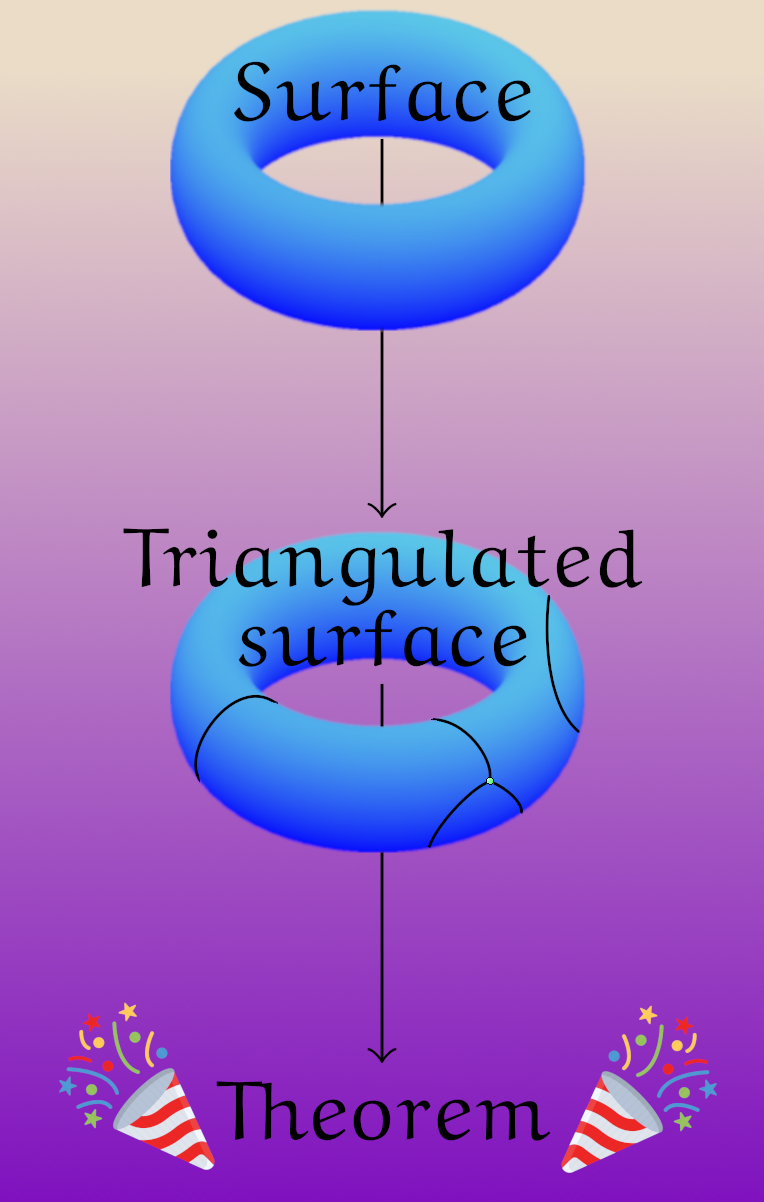
Properties:

  1. Powerful. Can prove many theorems (Miguel’s, Desargues’, Thales’…)

  2. Intuitive. Once the surface is chosen the proof just “falls out”.

  3. Rich. What happens if you glue two surfaces together? Does the genus affect the resulting theorem?

Conclusion

  • The topological proof gives a much richer view of the theorem landscape.

  • Our new theorem-generating algorithm which leads to many interesting questions (glueing, genus…).

  • So does a theorem have a shape?
    It’s an open question.

References

  1. Apel, Susanne, and Jürgen Richter-Gebert. 2010. “Cancellation Patterns in Automatic Geometric Theorem Proving.” In Automated Deduction in Geometry.

  2. Bobenko, Alexander I. 2020. “Projective Geometry Notes: Winter Semester 2016.” TU Berlin.

  3. Coxeter, H. S. M., and S. L. Greitzer. 1967. “Geometry Revisited.” 1st ed. Vol. 19. Mathematical Association of America. http://www.jstor.org/stable/10.4169/j.ctt19b9k65.

  4. Crapo, H., and Jürgen Richter-Gebert. 1995. “Automatic Proving of Geometric Theorems.” In. Springer, Dordrecht. https://doi.org/10.1007/978-94-015-8402-9_8.

  5. Hardiman, Leonard. 2020. “The shape of a theorem.” https://hidden-shapes.com.

  6. Richter-Gebert, Jürgen. 1993. “Mechanical Theorem Proving in Projective Geometry.” SC-93-05. Takustr. 7, 14195 Berlin: ZIB.

  7. ———. 2006. “Meditations on Ceva’s Theorem.” In The Coxeter Legacy: Reflections and Projections (Eds. Chandler Davis & Eric Ellers, American Mathematical Society, Fields Institute).

  8. ———. 2011. Perspectives on Projective Geometry: A Guided Tour Through Real and Complex Geometry. 1st ed. Springer Publishing Company, Incorporated.