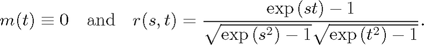MAGP (Example results)
Let X be a Gaussian process with mean and covariance functions denoted by:
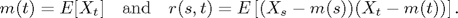
We assume regularity conditions imposed in Mercadier (2006).
Let M(a,b) denotes the maximum of X over the interval [a,b]:
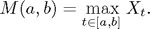
MAGP computes (by lower and upper bounds) the distribution of
the maximum M(a,b) when X is centered.
The estimation of
P[M(a,b)>u] is given by the command
magp(r,a,b,u,option). Consequently, this toolbox allows for
instance:
- the approximation of the pdf of M(a,b);
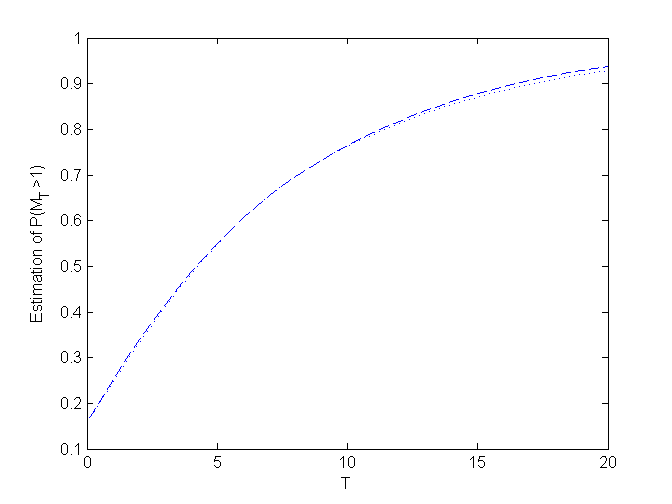
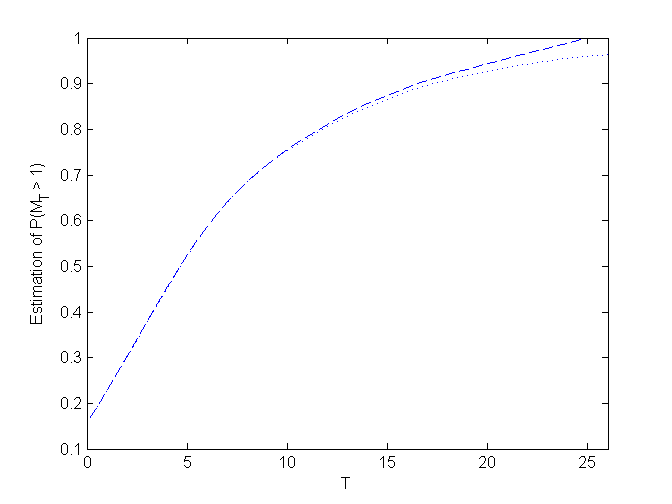
- the analysis of the behaviour of {M(0,T)>u} when T varies (see below);
- ...
Example 1 -- Stationary case with:
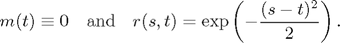
syms x y r=exp(-(x-y)^2/2); % Bounds for P( M(0,1)> 1 ): magp(r,0,1,1,500) ans = 0.2533 0.2541 % Plot the bounds of the function T -> P( M(0,T) > 1 ) obtained by MAGP: