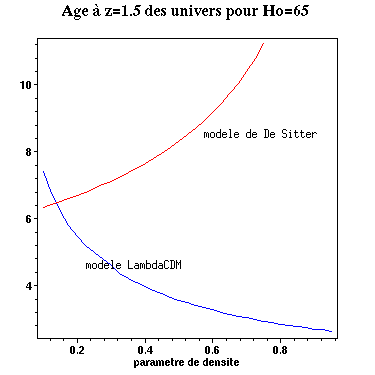
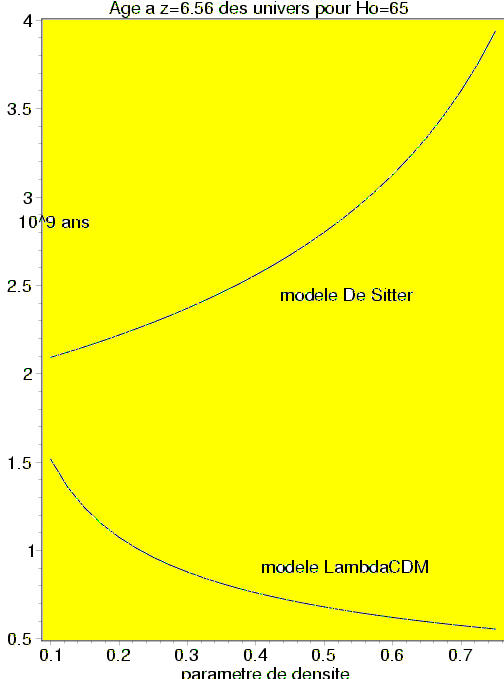
Voici l'âge des galaxies suivant leur redshift :
Pour le tracé des courbes, la formule simple à utiliser est classique.
Soit 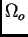 le paramètre de densité de matière dans les cadres
le paramètre de densité de matière dans les cadres
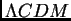 et
et 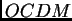 ,
,
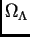 le paramètre de densité associé
à la constante cosmologique,
le paramètre de densité associé
à la constante cosmologique, 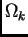 le paramètre de densité de courbure
défini par
le paramètre de densité de courbure
défini par
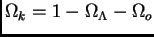 , alors l'âge d'un objet
observé à un redshift de z est :
, alors l'âge d'un objet
observé à un redshift de z est :
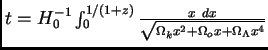 .
.
Si on note 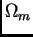 le paramètre de densité de la matière observée
aujourd'hui alors on obtient chacun des modèles suivants en posant :
le paramètre de densité de la matière observée
aujourd'hui alors on obtient chacun des modèles suivants en posant :
- pour 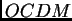 ,
,
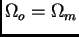 et
et
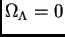 ;
;
- pour 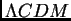 ,
,
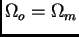 et
et
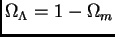 ;
;
- pour De Sitter,
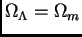 et
et 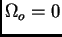 .
.
Nous avons négligé dans ces formules le paramètre de densité de radiation
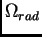 , mais cela ne modifie pas fondamentalement les résultats (sauf
pour les redshifts z plus grand que 1000).
, mais cela ne modifie pas fondamentalement les résultats (sauf
pour les redshifts z plus grand que 1000).
Tout lecteur attentif aura compris que le nouveau modèle
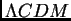 (paradime standard ?) n'est pas viable !
(paradime standard ?) n'est pas viable !
Par contre les modèles du type De Sitter passent l'épreuve aisément.
Ces modèles du type De Sitter admettent pour métrique :
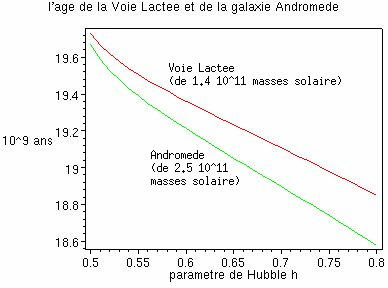
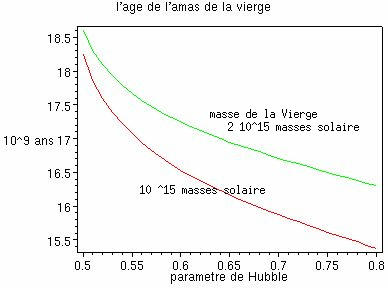
Passons maintenant à l'âge des surdensités locales dans l'univers proche.
Ces courbes sont construites à partir de ces modèles de De Sitter
dont la forme locale statique est :
De fait il est facile de montrer que cette forme (2) est l'approximation de toute
métrique d'univers.
Dans ce cadre Einsteinien, une surdensité de masse M se traduit par la métrique :
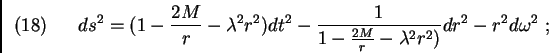
En résumé : l'étude locale de l'univers ne peut que reposer sur l'ensemble
suivant d'équations qui se déduisent de la métrique (18) :
Pour ceux qui souhaiteraient travailler dans un cadre post-Newtonien, les équations
ci-dessus peuvent se déduire du champ d'accélération suivant :
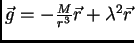


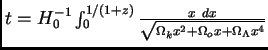 .
.
![]() ,
,
![]() et
et
![]() ;
;
![]() ,
,
![]() et
et
![]() ;
;
![]() et
et ![]() .
.
![]() , mais cela ne modifie pas fondamentalement les résultats (sauf
pour les redshifts z plus grand que 1000).
, mais cela ne modifie pas fondamentalement les résultats (sauf
pour les redshifts z plus grand que 1000).
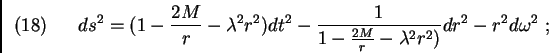
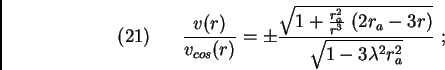
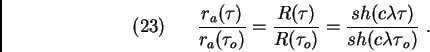
![]()