La métrique de De Sitter


et ses trois formes isotropes sur l'hyperboloide SO(1,4)/SO(1,3)
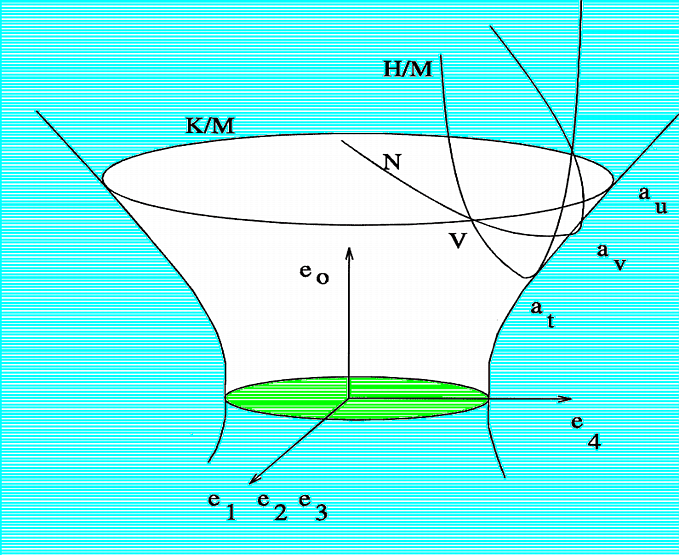
Dans le groupe de De Sitter G=SO(1,4), soient K=SO(4), H=SO(1,3),
M=SO(3) et N le sous-groupe R^4 de la décomposition d'Iwasawa.
La restriction à l'hyperboloïde G/H, dessiné ci-dessus, de la
métrique sur R^5, invariante par le groupe de De Sitter, nous donne
les trois types de modèles d'univers.

Pour en savoir plus un document en postscript est disponible en cliquant
sur la tulipe
 .
.







 .
.