La relativité
générale est-elle une théorie de la gravitation
ou un cadre géométrique ?

Les équations d'Einstein, un système de 10
équations à 10 inconnues, certes mais ...
Pourquoi oublie-t-on de dire que les inconnues sont des fonctions de
4 variables ?
En fait, il y a trop peu d'équations (les
équations d'Einstein) par rapport au nombre d'inconnues
(les coefficients à 4 variables de
la métrique). Certes il y a des conditions aux limites qui
permettent de déterminer des constantes d'intégration, mais elles ne
suffisent pas. On peut également utiliser le concept mathématique
de conditions de Cauchy, qui
permet d'obtenir des théorèmes d'unicité de solutions. Hélas,
ou heureusement ! même dans l'exemple de problèmes à symétrie
sphérique, on est loin de l'unicité. La relativité générale est un
cadre géométrique qu'il faut complèter pour
obtenir une théorie de la gravitation. Précisons un peu.
L'ambiguité de la relativité
générale est très rarement mise en évidence dans les ouvrages
sur la gravitation. Si cependant l'ambiguité sur la métrique
solution d'un problème est signalée et démontrée par certains
auteurs (c.f. S. Weinberg sections 7.4 et 7.5, ou encore par
S. Hawking et G. Ellis, chapitre 7) qui
montrent qu'il faut une jauge pour lever l'ambiguité de la
métrique, il est très rare de voir une
étude de l'ambiguité de la relativité générale du point
de vue des géodésiques suivies par les corps en chute libre (corps
d'épreuve). Il y a une croyance
disant que peu importe la métrique solution (peu importe la jauge),
les géodésiques sont les mêmes!
Cette croyance est
fausse, bien que fondée sur le concept de covariance, car elle s'appuie
sur l'ambiguité de l'expression "les géodésiques sont les
mêmes", expression traduisant à
la fois une covariance de nature locale (des équations des
géodésiques) et à la fois des contraintes associées à des
conditions aux limites (jamais covariantes).

Le plus rapide pour comprendre
l'ambiguité sur les géodésiques, est d'étudier le
problème le plus simple, les géodésiques dans un champ central
à symétrie sphérique (émis par une boule
"statique"). Par exemple, la période de rotation d'un satellite (corps
d'épreuve) dépend de la jauge choisie !
L'étude des géodésiques
montre, à l'évidence, qu'il faut une jauge pour confronter sans
ambiguité la relativité générale aux observations. A propos
de jauge, il est intéressant de revenir sur le travail de
K. Schwarzschild;
en fait on donne à tort son nom à une métrique
qui n'a rien à voir, sinon comme astuce technique, avec son travail.
La solution proposée par Schwarzschild provient d'une "jauge", celle de
déterminant un; de plus, K. Schwarzschild avait déjà signalé
en 1916, l'ambiguité de la relativité
générale dont les principes généraux avaient été établis 6 mois
plus tôt par A. Einstein.

"Dans la relativité générale,
à chaque fois qu'on fait un pas il faut s'arrèter pour
nettoyer ses chaussures." J.-M. Souriau.

Introduite très tôt, par De Donder en 1921 et Lanczos en 1922,
elle s'inscrivait dans la problématique du
moment, à savoir trouver un "meilleur système de coordonnées".
Elle s'appelle toujours "condition des coordonnées harmoniques",
dénomination pas très heureuse car celà cache sa signification de
jauge.Une fois une jauge écrite
dans un système privilégié de coordonnées, il est tout à
fait possible de la transcrire de manière covariante;
ceci est un fait bien connu. Ainsi toute jauge peut et doit s'écrire de
manière covariante. C'est Logunov qui est le premier, à ma
connaissance, à écrire la jauge harmonique de manière
covariante.
Justifications diverses de la jauge harmonique :
1- Par analogie avec l'électromagnétisme;
Dans cette théorie la jauge de Lorentz est incontournable, par une
présentation similaire de l'electromagnétisme et de la gravitation, la
condition dite de "coordonnées harmoniques" est établie.
2- Le champ gravitationnel se propage à la
vitesse de la lumière car la jauge harmonique préserve le
d'Alembertien.
3- Les lois de conservation peuvent s'écrire sous forme
intégrale c.f. V. Fock.
4- Le formalisme P.P.N. (i.e. l'approximation
post-Newtonnienne) qui seul peut permettre l'interprétation des
résultats d'observation, nécessite la jauge harmonique c.f. S.
Weinberg chap. 9.4.
5- Si le champ gravitationnel est transporté
par le graviton (supposé de masse nulle et de spin 2) alors toute
métrique traduisant un champ gravitationnel vérifie la jauge
harmonique. C'est un théorème sur les représentations du groupe
de Poincaré. Plus précisément, si l'on considère la représentation
du groupe de Poincaré, i.e. le groupe des invariants de l'espace de
Minkowski, dans l'espace des deux-tenseurs symétriques elle contient des
représentations de spin 2, 1 et 0; aussi si
l'on veut un champ gravitationnel qui ne soit pas transporté par une
particule de spin 1 (le photon), i.e. compatible avec l'électromagnétisme,
il faut restreindre cette représentation au sous-espace des
deux-tenseurs symétriques tels que cette représentation ne contienne
pas la représentation de spin 1, ce qui impose des équations
d'orthogonalité.
6- L'étude des ondes gravitationnelles est
toujours faite dans un système de coordonnées harmoniques; la
justification souvent donnée vaut son pesant de gratons (comme on dit
à Lyon) :
les calculs sont plus simples!
Les justifications 1, 2 et 3 sont heuristiques, par contre les
justifications 4 et 5 sont importantes.

Nul doute que dans un
proche avenir on puisse tester la validité de la jauge
harmonique.

Il est communément admis que toute étoile ou astre a une vie, qui
après différentes phases (séquence principale, géante rouge,
novae ou supernovae , etc... ), devient un astre mort, un "déchet"
froid ne pouvant plus trouver en son sein un regain de vitalité. Les
astronomes et astrophysiciens disent même que tout soleil évoluera
vers une situation très stable finale du type naine blanche ou étoile
à neutrons ou encore "trou noir" suivant la masse de cette étoile. Nous
avons donc des objets limites, qui dans la mesure où ils n'évoluent
plus, peuvent être considérés sous le seul point de vue gravitationnel.
PAGE EN COURS DE REDACTION
En utilisant la jauge harmonique, nous obtenons :
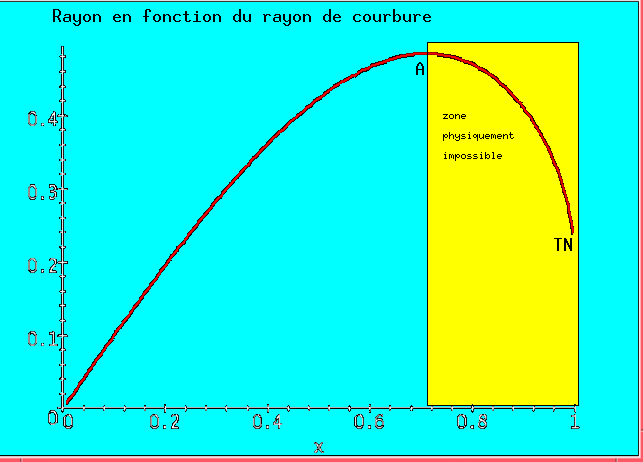
c'est-à-dire, la limite trou noir ne peut pas être
approchée suite à un effondrement gravitationnel !
Il est à signaler que pour une étoile à neutrons,
nous trouvons le même
ordre de grandeur de masse critique que celui utilisé dans la
littérature obtenu à partir de considérations d'équilibre
interne.







