Is general
relativity a theory of the gravitation
or a geometrical framework?

The Einstein equation is a system of 10
equations of 10 unknown functions, certainly but...
Why does one forget to say that the unknown functions are related to
4 variables?
In fact, there are not enough equations (the ten Einstein
equations) compared to the number of unknown functions
(coefficients of the 4 variables
of the underlying space-time). Admittedly there are boundary conditions which
makes it possible to determine constants of integration, but they
are not enough. One can also use the mathematical concept
of Cauchy conditions, which
makes it possible to obtain theorems upon the unicity of solutions. Alas,
or fortunately! even in the example of problems with spherical
symmetry, one is far from unicity. General relativity is
a geometrical framework which must be completed
to obtain a theory of the gravitation. Let us specify a little.
The ambiguity of general
relativity is very seldom highlighted in the works
on the gravitation. So however this ambiguity on metric
solutions of a given problem is announced and shown by some
authors (c.f. S. Weinberg sections 7.4 and 7.5, or by
S. Hawking and G Ellis, chapter 7, ...) who
shows that one needs a gauge to raise the ambiguity of
the metric, it is very rare to read
a study about the ambiguity of the general relativity from
the point of view of geodesics followed by the bodies in free fall
(test body). There is a belief
saying that it does not matter the metric solution (it does not matter the gauge), the geodesics are the same !
This belief is
false, although founded on the concept of covariance, because it is based
on the ambiguity of the expression " the geodesics are
the same ", this expression translating
at the same time a covariance of local nature (of the equations of
the geodesics) and at the same time of the constraints associated with
boundary conditions (never covariant).

Fastest to understand
the ambiguity on the geodesics, is to study
the simplest problem, the geodesics in a central field
with spherical symmetry (emitted by a "
static " star). For example, the period of rotation of a
satellite (test body) depends on the selected gauge!
The study of geodesics
shows, obviously, that one needs a gauge to confront without
ambiguity general relativity to the observations.
In connection with gauge, it is interesting to reconsider the work of
K Schwarzschild;
in fact one wrongly gives his name to metric
which does not have anything, if not like technical easy way,
with his work.
The solution suggested by Schwarzschild comes from a " gauge ", that of
determinant one; moreover, K Schwarzschild had already announced
in 1916, the ambiguity of the general
relativity whose general principles had been established 6 months
earlier by A. Einstein.

" In general relativity,
each time that a step is made one needs to stop
and clean its shoes." J.-M. Souriau.

Introduced very early, by Donder in 1921 and Lanczos in 1922,
it fell under the problematic of
the moment, namely to find a " better frame of reference ".
It is always called " the harmonic co-ordinates condition ",
this name being not very happy because it hides its significance of
gauge. Once a gauge is written
in a privileged system of co-ordinates, it is
fully possible to transcribe it in a covariant manner,
this is a well-known fact. Thus any gauge can and must be written in a
covariant form. It is Logunov which is the first, to my
knowledge, to write the harmonic gauge in a covariant form.
Various justifications of the harmonic gauge:
1 By analogy with electromagnetism;
In this theory the gauge of Lorentz is impossible to circumvent, by
a similar presentation of the electromagnetism and gravitation,
the condition known as of " harmonic co-ordinates condition "
is established.
2 The gravitational field is propagated at
the speed of the light because the harmonic gauge preserves
the d' Alembertian.
3 The 3 conservation laws can be written in integral
form c.f. V Fock.
4 P.P.N. formalism (i.e. the
post-Newtonnian approximation ) which only can allow the interpretation of
the results of observation, requires harmonic gauge cf. S.
Weinberg chap. 9.4.
5 If the gravitational field is transported
by the graviton (supposed of null mass and spin 2) then very
metric translating a gravitational field checks the harmonic
gauge. It is a theorem on the representations of the Poincaré group.
More precisely, if one considers the representation
of the Poincaré group, i.e. the group of the invariants of the
Minkowski space, in the space of the symmetrical two-tensors it contains
representations of spin 2, 1 and 0; therefore if
one wants a field gravitational which is not transported by
a particle of spin 1 (the photon), i.e. compatible with electromagnetism,
it is necessary to restrict this representation with the subspace of
the symmetrical two-tensors such as this representation does not contain
the representation of spin 1, which imposes orthogonality equations, so
the harmonic co-ordinates condition.
6 The study of the gravitational waves
is always made in a harmonic frame of reference;
the often given justification ...
the computations are simpler!
Justifications 1, 2 and 3 are heuristic, on the other hand
justifications 4 and 5 are significant.

There is no doubt that in the near future
one can test the validity of the harmonic gauge.

It is commonly allowed that any star has a life, which
after various phases (principal, red giant,
novae or supernovas, etc...), becomes a died star, a cold " waste
" not being able more to find in its center a renewal of vitality.
The astronomers and astrophysicists even say that any sun will evolve
to a very stable type of matter, for exemple white dwarf, neutron star
or ... according to the mass of this star. We
thus have limiting objects, which insofar as they do not evolve
any more, can be considered under the only gravitational point of
view.
PAGE IN THE COURSE OF DRAFTING
So, using the harmonic gauge, we obtain :
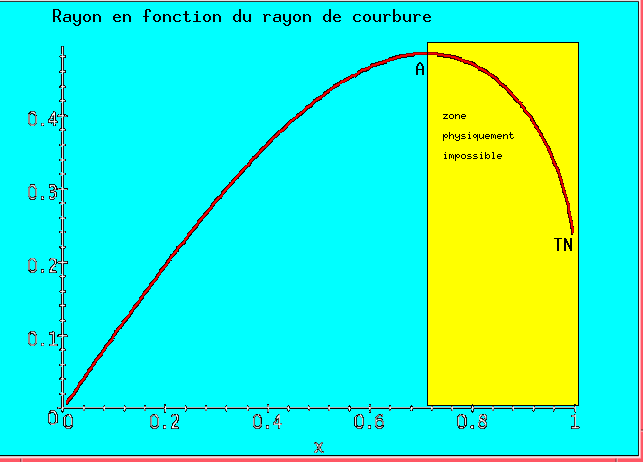
insofar a gravitational collapse could never lead to a black hole !
It is to be underline that for a neutron star,
we find the same
order of magnitude of critical mass as that obtained in
the literature starting from equilibrium considerations.
If you want the proofs click here :









