L'oscillateur et la jauge harmonique

Michel Mizony, IGD

Institut Girard Desargues (UMR 5028 CNRS), Université lyon 1
43, bd. du 11 Novembre 1918, 69622 Villeurbanne cedex
e-mail: mizony@desargues.univ-lyon1.fr

Un exemple de mécanique qui pose question

Sur la problématique de l'oscillateur harmonique (pendule simple ou ressort). Plaçons-nous dans le contexte d'un des plus simples des systèmes mécaniques : celui du système masse-ressort idéal, à petites oscillations, soumis à une force extérieure F(t). L'équation du mouvement de la masse est traditionnellement écrit sous la forme $\ddot{x}+Kx-F(t)=0$ , ou K est une constante associée au ressort. Expérimentalement les mécaniciens se sont vite aperçus qu'il existait un terme complémentaire en x , appelé force de " frottement " plus précisément force de dissipation, du fait qu'il est proportionnel à la vitesse, et ce bien qu'il n'existe aucune source de frottement. On a donc l'équation $\ddot{x}+ \alpha \sqrt{K}\dot{x} +Kx-F(t)=0$, où $\alpha$ est bien mesuré. Mais des expériences plus fines, lors d'études sur l'amortissement en régime transitoire rapide, montrent qu'il faut remplacer ce coefficient $\alpha \sqrt{K}$ par une fonction $\gamma (t) = \alpha \sqrt{K} + \beta t +...$ ; et le coefficient $\beta$ commence à être bien mesuré. Le problème est donc le suivant : Soit $\ddot{x}+ \gamma\dot{x}+ Kx -F(t)=0$ cette équation du mouvement, comment obtenir théoriquement cette fonction $\gamma$. Question ouverte, mais importante. En effet, il est une expérience que l'on fait souvent, celle de constater que la plupart des pannes mécaniques interviennent pendant la mise en route ou lors de l'arrêt d'un système. Peut-on limiter les sources de ces pannes qui proviennent lors d'un changement de régime brutal (changement de régime modélisé par notre force extérieure $F(t)$, par exemple de la forme $Asin(w(t)))$. Il semble important de connaître $\gamma$ en fonction de F, pour mieux comprendre certaines causes de pannes. En régime normal, on sait qu'il suffit d'éviter des plages de résonances, mais le problème reste incompris en régime transitoire (démarrage, arrêt, ou ... panne secondaire qui perturbe soudainement le régime normal). De fait avec des collègues de l'INSA de Lyon (Ahmad Al Majid et Régis Dufour) nous avons cette année trouver un premier résultat, i.e. la piste de modélisation qui semble bonne à l'épreuve des expérimentations ; cette piste est basée sur le fait que le temps propre de la pièce mobile n'est pas forcément celui des pièces fixes (autrement dit celui du laboratoire), ce qui oblige à utiliser toute la théorie tensorielle de la relativité générale. Même si les vitesses en jeu ne sont pas relativistes, il se trouve que les phénomènes vibratoires liés à des régimes transitoires rapides nécessitent de recourir au temps propre. C'est ce que viennent de montrer Ahmad Al Majid et Régis Dufour du laboratoire de Mécanique des Structures, UMR CNRS 5006 de l'INSA de Lyon cf. [1], qui ont mis en évidence l'existence d'un temps propre de la pièce mobile.

Remarque : bien des problèmes que l'on croit bien modélisés ne le sont pas.

En examinant les résultats expérimentaux, Ahmad est parti de l'idée simple qui consiste à se poser la question de savoir si le temps propre d'une pièce en mouvement était bien le même que celui de l'observateur fixe (expérimentateur). Aussi a-t-il introduit un tenseur métrique et trouvé des solutions telles que l'une des équations des géodésiques avait la forme théorique voulue. Une des solutions était même assez bonne du point de vue expérimental. Mais cette solution a un gros inconvénient, celui de paraître une solution ad hoc. Un traitement systématique s'imposait donc.

Sur le calcul tensoriel. L'on sait que pour assurer l'unicité de solution pour un problème de gravitation, dans le cadre de la relativité générale, il faut une jauge (des équations complémentaires), cf. V. Fock par exemple. La jauge prise usuellement est la jauge harmonique, souvent appelée ``système de coordonnées harmoniques''. A part des justifications théoriques du type le graviton est de spin 2, ou le mouvement d'un front d'onde s'écrit très simplement, il n'y a pas encore à ce jour de véritables vérifications de cette jauge. A l'aide de la puissance des ordinateurs et de logiciels de Calcul Formel (Maple), nous avons dans un premier temps cherché toutes les 2-métriques ${\it g}=\left [\begin {array}{cc} \tau(t,x)&\,f(t,x)\\ \noalign{\medskip }f(t,x)&-h(t,x)\end {array}\right ]$ telles que l'une des équations des géodésiques soit de la forme voulue. Evidemment il y a beaucoup, énormément de solutions. Puis nous avons cherché celles qui de plus vérifient les équations de la jauge harmonique. Le résultat est là, qui résiste à l'expérimentation.

Formulation tensorielle

Voici les résultats de calcul tensoriel (obtenus avec le logiciel Maple) dont nous aurons besoin.
Soit $(t,x)$, l'espace-temps de l'observateur qui regarde les oscillations du système. Pour cet observateur la métrique est la métrique canonique $grr$ de Lorentz. Soit $g$ la métrique associée à la masse qui oscille. Prenons son écriture dans la carte associée à l'observateur; elle est de la forme $\left [\begin {array}{cc} \tau(t,x)&\,f(t,x)\\ \noalign{\medskip }f(t,x)&-h(t,x)\end {array}\right ]$. Mais pour obtenir des équations ``simples'', il est pratique de la prendre sous la forme ${\it g(t,x)}=h(t,x)\left [\begin {array}{cc} \tau(t,x)&1/2\,f(t,x)\\ \noalign{\medskip }1/2\,f(t,x)&-1\end {array}\right ]$, avec pour conditions initiales au point $(0,0)$ : ${\it g(0,0)=grr(0,0)=\left [\begin {array}{cc} 1&0\\ \noalign{\medskip }0&-1\end {array}\right ]}$, (absence de force extérieure $F$). Pour une 2-métrique le tenseur d'Einstein est toujours identiquement nul, ce qui correpond au cadre expérimental (les forces de gravitations s'exercant sur la pièce mobile sont négligeables).

Une des équation du mouvement peut se mettre sous la forme :

$$\ddot {x}+\frac{1}{2}\frac{h'}{h} {\dot {x}}^2+\frac{\dot h}{... ...au \frac{h'}{h}-\frac{1}{2}f\frac{\dot h}{h}=0\ \ \ \ \ \ \ (1)$$

l'autre équation étant l'intégrale première du mouvement, est donnée par la métrique :

$$h (\tau+f\dot x - {\dot x}^2 ) =1\ .$$

Ecrivons maintenant les deux équations provenant de la jauge harmonique écrites de manière ${grr}$-covariante : elles s'obtiennent en calculant : $D_{\mu}(\sqrt{\frac{g}{grr}} g^{\mu \nu}) = 0$ où $D_{\mu}$ est la dérivation covariante par rapport à la métrique plate ${grr}$

Lemme 1 : Les équations provenant de la jauge harmonique sont:

$$\{\ \dot \tau=\,f'\,\tau \,-f\dot f ,\ \ \tau '\,=\, \dot f\ \}\ .$$

D'après ce lemme 1, pour $u(t,x)$ telle que $\dot {u}=\tau$ et $u'=f$, alors la métrique $g$ s'écrit :

théorème 1 :

$${\it g(t,x)}=h(t,x)\left [\begin {array}{cc}\dot {u}(t,x) &1/... ...'(t,x)\\ \noalign{\medskip }1/2\,u'(t,x)&-1\end {array}\right ]$$

et vérifie la jauge harmonique si et seulement si u est solution de l'équation :

$$(*)\ \ \ \ {\frac {\partial ^{2}}{\partial {t}^{2}}}u(t,x)-\l... ...\right ){\frac {\partial ^{2}}{\partial t\partial x}}u(t,x)=0.$$

Il ne reste plus qu'à résoudre cette équation pour déterminer $f(t,x)=u'(t,x)$ (et par suite $\tau$). Pour cela, posons $u(t,x)=\sum _{i=0}^{\infty }u_{i}(t){x}^{i}$. Alors l'équation (*) se réduit au système d'équations

Lemme 2 : pour $i \geq 0$:

$$u_{i+2}(t)=\frac {\ddot{u}_{i}(t)+\sum _{j=1}^{i+1}j(i+3-2j)u_{j}\dot{u}_{i+2-j}}{(i+1)(i+2)\dot{u}_{0}(t)}\ ,$$ (1)

Formulation Lagrangienne

Il est évidemment tentant de poser tout de suite $h'=0$ et $-\frac{1}{2}f\frac{\dot h}{h}=Kx-F(t)$; et de fait dans le processus de résolution du problème, c'est bien ce que nous avons fait, avant de mettre en évidence les résultats ci-dessus. Mais restons dans un cadre général, en examinant la formulation Lagrangienne du problème.
Le Lagrangien classique est

$$\frac{1}{2}m{\dot x}^2-( \frac{1}{2}Kx^2-F(t)x)$$

et pour tenir compte du temps propre, nous avons introduit un facteur conforme en prenant:

$$L=e^{\nu (t,x)} (\frac{1}{2}m{\dot x}^2-( \frac{1}{2}Kx^2-F(t)x))$$

dont l'équation du mouvement, donné par $\frac{d}{dt}(\frac{\partial L}{\partial \dot x})- \frac{\partial L}{\partial x}$, s'écrit

$$m\ddot x +\frac{m}{2}\nu '{\dot x}^2 +m\dot \nu {\dot x} +Kx-F(t)\ +\nu ' ( \frac{1}{2}Kx^2-F(t)x) \ \ \ \ \ \ (2)$$

Cette équation (2) ressemble beaucoup à l'équation (1) obtenue dans le cadre tensoriel, en remplaçant K par K/m, F par F/m et en posant

$$e^{\nu (t,x)}=h(t,x).$$

Mais dans ce cadre Lagrangien, comment trouver ce facteur conforme ? Il manque des équations. Le cadre tensoriel en fournit, mais ces équations sont diffiles à obtenir (même avec l'aide de la puissance du calcul formel). Et si il y a deux dimensions d'espace au lieu d'une, je ne sais pas faire grand chose.

En résumé, le cadre Lagrangien nous donne rapidement l'équation fondamentale du mouvement et le cadre de la relativité générale les équations supplémentaires nécessaires, à partir des équations de la jauge harmonique.

Résultats pour l'oscillateur harmonique

Revenons dans la situation de l'expérimentation faite; les vitesses ($\dot x$) sont très petites, aussi nous allons négliger les termes en ${\dot x}^2$ dans les équations (1) et (2) tout simplement en prenant $h'=\nu '=0$ et en posant $\gamma(t)= \dot {\nu}= \frac{\dot h}{h}$.
L'équation du mouvement se réduit à

$$\ddot {x}+ \gamma (t)\dot {x}+ Kx -F(t)=0\ ,$$

avec

$$- \frac{1}{2}f(t,x(t)\ \frac{\dot h}{h} = Kx(t) -F(t)$$

pour la solution $t\rightarrow x(t)$ de l'équation du mouvement vérifiant les conditions initiales $x(0)=\dot x(0)=0$. Nous allons aussi tenir compte des conditions aux limites en particulier celle qui stipule que si la force F(t) est périodique ( $F(t)=A\ sin(\omega t)$) alors l'équation du mouvement se réduit à $\ddot{x}+ \alpha\ sqrt(K)\dot{x}+ Kx -F(t)=0$.
Il reste donc à calculer $\gamma(t)$ en fonction de $K$, $F(t)$, en utilisant la jauge harmonique, i.e. le lemme 2.

Corollaire :
Sous l'hypothèse de la jauge harmonique, l'équation différentielle du mouvement de l'oscillateur harmonique contient un terme d'amortissement (ou de dissipation) dont le coefficient $\gamma(t)$ admet le développement limité à l'ordre 4 suivant lorsque $F(0)=0$ et $\dot {F}(0) \neq 0$:

$$\gamma(t)=\alpha\,\sqrt{K}(1+\frac{t}{2}\frac{\ddot F(0)}{\do... ...dot F}(0)\ddot F(0)+ K \ddot F(0)\dot F(0)}{\dot F(0)^2}+ ... )$$

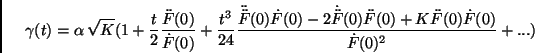
La preuve ne pose pas de difficultés, mais pour les calculs pénibles il est intéressant de recourir à un logiciel de calcul formel.

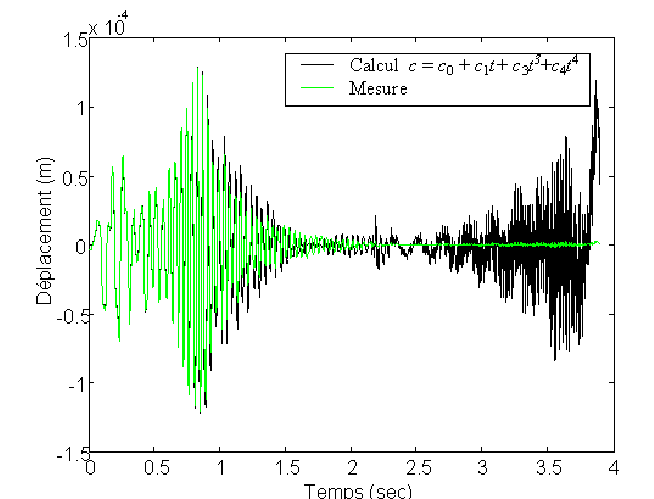
Voici ce que donne la confrontation à l'expérimentation (réalisée par A. Al Majid à l'INSA de Lyon).
Pour les figures $\gamma(t)$ est noté $c(t)=co+c1*t+c3*t^3+c4*t^4$.



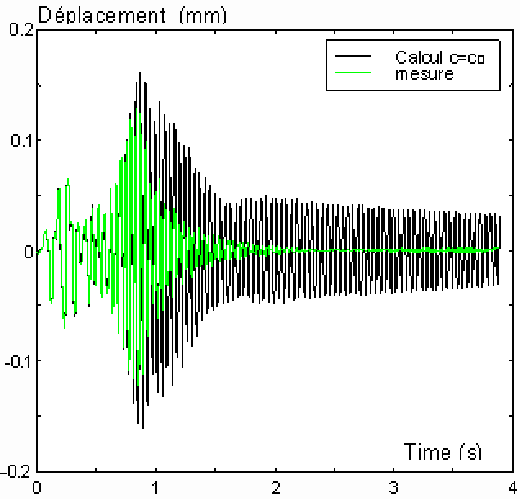
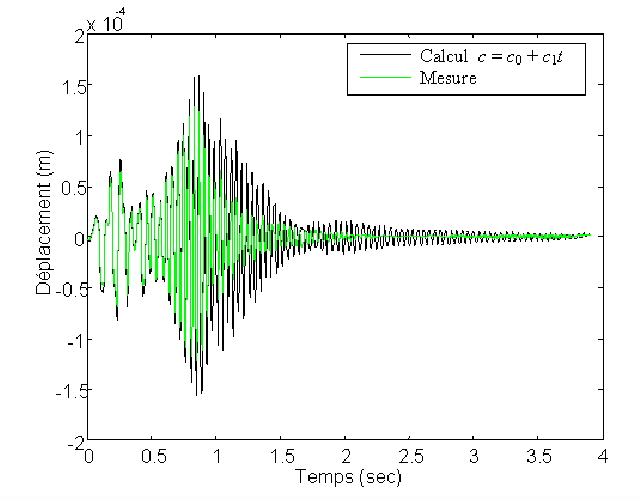
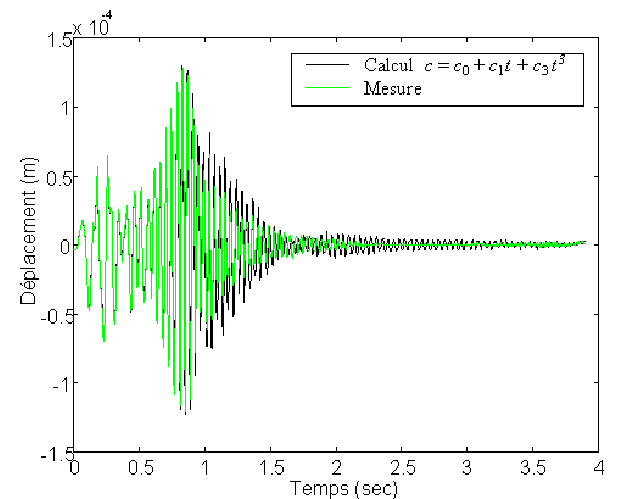
Il est manifeste que l'adéquation entre la courbe expérimentale et la courbe théorique augmente avec l'ordre du développement limité. A l'ordre suivant cette adéquation est encore meilleure dans un premier temps, puis se manifeste sans doute un problème d'instabilité dans la résolution numérique.

Remarques en vrac
1- Au niveau de la confirmation expérimentale, les premiers résultats sont probants, mais ils restent à les conforter. La question de la compréhension de ce coefficient de dissipation $\gamma$ à travers le concept de temps propre reste à approfondir. De fait, dans le cadre d'un régime transitoire rapide, l'amortissement peut être modélisé comme phénomène métrique.
2- Il reste à comprendre pourquoi la jauge harmonique est essentielle pour de simples problèmes de mécanique. Est-ce lié au fait que la force extérieure se transmet à la vitesse de la lumière, ou plus profondemment à une invariance du mouvement de tout ``front d'onde'' dans la terminologie de Vladimir Fock ?
3- On sait que le groupe de Poincaré est fondamental au niveau de la relativité restreinte et générale, ainsi qu'au niveau de la mécanique quantique, pourquoi ne jouerait-il pas un rôle à l'échelle intermédiaire de la mécanique usuelle ? En fait la jauge harmonique possède un rapport étroit avec ce groupe de Poincaré.
4- Relativisons. Ceci n'est évidemment qu'un début, et pour plusieurs raisons : la constante K n'est constante qu'à une première approximation; les mouvements de l'oscillateur sont supposés petits; nous avons regardé un problème à une seule dimension spatiale; enfin nous avons supposé que le coefficient de dissipation $\gamma$ ne dépend que de t (en négligeant l'aspect relativiste des vitesses).
5- Au risque de me répéter, sans la puissance de calcul des ordinateurs, et celle du logiciel ``Maple'', je n'aurais pas pu trouver que la forme à adopter pour le tenseur métrique soit : ${\it g(t,x)}= \left [\begin {array}{cc} \tau(t,x)h(t,x)&1/2\,f(t,x)h(t, x)\\ \noalign{\medskip }1/2\,f(t,x)h(t,x)&-h(t,x)\end {array}\right ]$.
6- Une certitude : pour espérer traiter de manière similaire l'étude de phénomènes vibratoires dans le plan ou l'espace, on ne peut pas faire l'économie de la traduction de la jauge harmonique dans le cadre Lagrangien.
7- Une deuxième certitude : l'oscillateur harmonique nous fournit un test d'un aspect de la relativité générale (celui de la pertinence de la jauge harmonique), un test en laboratoire sur terre, de plus extrèmement peu couteux financièrement, et renouvellant le problème de l'étude de la limite entre mécanique classique et mécanique relativiste.

A. Al Majid et R. Dufour ``An Event Dimension for Modeling Damping Due to Time-Varying Forcing Frequency'', in Nonlinear Dynamics, Kluwer Academic Publishers, 2000.
A. Al Majid et R. Dufour : " Modelling damping effect due to high transient motion using the Riemannian space " ; ASME, Pittsburg (Pennsylvanie), Septembre 2001.
V.Fock, ``The theory of space, time and gravitation'', Pergamon Press, 1961;
M. Mizony et G. Arsac ``Que peut nous apprendre la gravitation sur l'espace-temps?'' preprint de l'Institut Girard Desargues (UCBL), no 12, juillet 1998.
M. Mizony ``la relativité générale aujourd'hui'', preprint du Laboratoire d'Analyse Fonctionnelle et Probabilités (UCBL), no 12, octobre 1993.