 L'Effet Pioneer et les formes de métrique de l'univers
L'Effet Pioneer et les formes de métrique de l'univers
L'accélération anormale de Pioneer est-elle normale ? est-ce l'effet des coordonnées locales,
autrement dit, provient-elle d'une correction cosmologique au champ émit
par notre Soleil ?
Pour les preuves et développements voir : Cosmological effects in the local static frame, Michel Mizony et Marc Lachièze-Rey, Novembre 2004,
à paraître dans Astronomy and Astrophysics, (gr-qc/0412084).

INTRODUCTION : Dans les articles traitant de l'"accélération anormale" des sondes Pioneer,
cette accélération, notée "a_p", obtenue à partir de redshift observés, est exprimée en
terme d'une accélération (celle de la longueur du trajet subit par les signaux émis par la sonde).
Cette accélération a_p est donc décrite comme conséquence d'un champ post-newtonien, tout simplement pour
pouvoir évaluer les influences conventionnelles pouvant s'exercer sur la sonde
(effet de rotation, de pression de radiation, ...).
Par exemple, dans l'article de Mbelek et Michalski (gr-qc/0310088), l'étude des "spin" des
satellites Pioneer10 et Pioneer11 permet aux auteurs d'évaluer cette "accélération anormale"
à :
a_p=(7.84 +,- 0.01) 10^(-8)cm/(s^2).
Il a été remarqué que cette "accélération anormale" a_p est de l'ordre de grandeur de la
constante de Hubble qui traduit l'expansion de l'univers.
Peux-t-on valider ou invalider simplement cette assertion ?
Si elle est vraie alors la valeur locale (dans le système solaire) de la constante de
Hubble est environ de :
H_o=75km/s/Mpc.
Si elle est fausse alors cette accélération reste encore non comprise donc "anormale".
Sur les formes de métriques de l'univers
Dans des notations usuelles, la métrique d'univers s'exprime dans les coordonnées comobiles
(tau, alpha) par
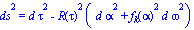
Si on veut de plus que cette métrique s'exprime dans une forme localement inertielle au point
ici et aujourd'hui (tau_o, 0) on a :
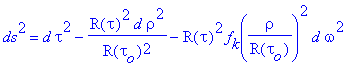
Avec cette forme de métrique on obtient immédiatement la formule exprimant
le redshift cosmologique z et la vitesse radiale, que l'on notera Vl, d'un signal lumineux
(ou radio) émis
par un corps comobile se trouvant au point (tau, rho) :
Vl(tau,rho)= 1 + z = R(tau_o)/R(tau)= d tau_o/d tau
De ce résultat, on obtient immédiatement une première formule de base :
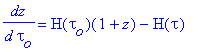 En posant
En posant 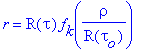 , on obtient la forme de métrique
suivante dans les coordonnées (tau,r):
, on obtient la forme de métrique
suivante dans les coordonnées (tau,r):
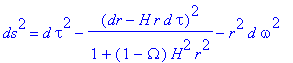
Exprimons la formule du redshift et de la vitesse d'un signal émis d'un corps en chute
libre cosmologique, vitesse écrite
dans ces coordonnées (tau,r); on a d'une part
Vl(tau,r)=Vl(tau,r(tau,rho))=Vl(tau,rho)=1+z
et d'autre part en utilisant la dernière forme de métrique :
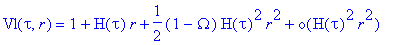
On retrouve ainsi une formule classique du redshift émis en un point (tau,r) par un corps
en chute libre dans les coordonnées cosmologiques (tau,rho) :
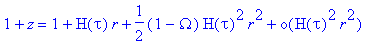 C'est la deuxième formule de base permettant de bien poser le problème de l'accélération
anormale notée a_p des sondes.
C'est la deuxième formule de base permettant de bien poser le problème de l'accélération
anormale notée a_p des sondes.
Des deux formules de base on obtient alors en première approximation :
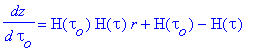
Si tout le monde est d'accord pour dire que cette accélération se calcule à
partir de dz/dtau, deux écoles s'expriment et divergent sur la manière de mener ce calcul.
En effet dans la deuxième formule de base on a r=r(tau) qui décrit une trajectoire.
1- Est-ce celle de la sonde, dans ce cas sa vitesse (cosmologique) dr/dtau=H*r en
première approximation et donc dz/dtau est de l'ordre
de H^2 r, c'est-à-dire
l'effet Pioneer ne s'explique pas à partir
d'une correction cosmologique.
2- Est-ce celle des signaux émis en direction du soleil, dans ce cas dr/dtau=- Vl(tau,r)
et cette
correction cosmologique explique complètement l'effet Pioneer;
et même
a_p serait plus précisément
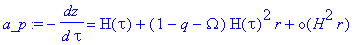 Cette deuxième interprétation est fréquente dans la littérature, car
l'accélération a_p traduirait, via des mesures de fréquences, "la vitesse de changement
de la longueur de la trajectoire du signal reçu puis réémit par la sonde observée".
Cette deuxième interprétation est fréquente dans la littérature, car
l'accélération a_p traduirait, via des mesures de fréquences, "la vitesse de changement
de la longueur de la trajectoire du signal reçu puis réémit par la sonde observée".
Une lecture attentive de la définition de a_p montrerait, semble-t-il, que la première
interprétation est la bonne : et donc un développement
limité sur H dans dz/dtau_o, donne la contribution cosmologique a_p_cosmo, négligeable
pour les sondes :
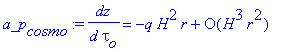
L'EFFET PIONEER RESTERAIT DONC "ANORMAL"
Mais une lecture plus attentive, montre que implicitement il est supposé que la vitesse des signaux est
invariante (car égale à c, la vitesses de la lumière). Or le fait que la vitesse de la lunière soit une
constante (fondamentale) dans le vide et que la vitesse de la lumière soit covariante (ds=0) n'est pas du tout
incompatible avec le fait qu'elle soit "variable" par rapport à un système de coordonnées fixé (cf. la formule
ci-dessus de Vl(tau,r)).
En clair cela signifie que la variation dz/dtau du redshift mesurée a deux composantes :
- d'une part celle due à l'accélération proprement dite de la sonde (accélération liée à l'expansion de l'univers)
donnée par la formule a_p_cosmo,
-d'autre part celle due à la variation de la vitesse de la lumière (provenant de Vl(tau,r).
Ainsi a_p est la somme de ces deux contributions.
TOUT EST DONC BIEN NORMAL.
Mais nous n'avons considéré que l'effet cosmologique pur, sans tenir compte de la masse du soleil.
Pour examiner l'influence du soleil, écrivons une forme locale de la métrique d'univers,
que l'on nomme (Marc Lachièze-Rey et moi) la forme osculatrice hic et nunc
de la métrique d'univers. Elle s'obtient en posant tau=h(t,r), avec h(t,0)=tau, et en cherchant
la fonction h pour éliminer le terme croisé dans la métrique d'univers exprimée dans les coordonnées
locales (t,r). On obtient :
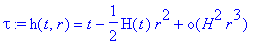
et donc
la métrique osculatrice de l'univers, dépendant des 3 paramètres cosmologiques
Omega, H et q,
(cette métrique est exacte pour les modèles d'univers de De Sitter pour lesquels Omega =-q) :
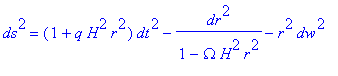
Le domaine de validité de cette forme de métrique est donné par Hr<1, donc r< 4000 Mpc environ.
On peut calculer alors la métrique d'univers locale avec une masse M à l'origine; (exacte pour Omega =-q)
et approchée à l'ordre 2 en M/r et 3 en H r :
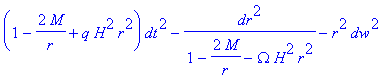
On calcule alors les géodésiques radiales et on obtient la
trajectoire d'un mobile
qui part d'un point ro animé d'une vitesse vo; et comme l'élément de distance lumineuse
dl est égal à dl=L/F dr, où L et F sont les racines carrées des coefficients de la
métrique ci-dessus on a
1+z=L/F dr/dt et on obtient :
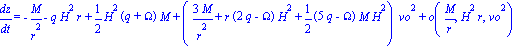

Ainsi l'effet Pioneer, l'accélération "anormale" en direction du soleil,
constatée sur différents satellites (Galiléo, Pioneer 10 et 11), à travers des observations
de signaux radios, n'est toujours pas expliquée par l'accélération propre du satellite
(accélération d'origine cosmologique); cependant si l'on considère les géodésiques
lumineuses "radiales", pour chacune des formes de la métrique d'univers et si on note V la "vitesse"
de la lumière dans ces coordonnées, il est surprenant de constater que l'on a une
"accélération" de la lumière de
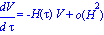 Et si ce n'était pas tout simplement cette accélération cosmologique de la "vitesse"
de la lumière qui est mise en évidence ? Cet exemple montre qu'il est important de ne pas confondre
l'invariance de la vitesse limite c, (celle de la lumière si le photon est effectivement de masse nulle) et
la vitesse d'un signal lumineux dans un système de coordonées fixé (en clair un système géocentrique ou héliocentrique pour
les mesures du redshift des satellites incriminés).
Et si ce n'était pas tout simplement cette accélération cosmologique de la "vitesse"
de la lumière qui est mise en évidence ? Cet exemple montre qu'il est important de ne pas confondre
l'invariance de la vitesse limite c, (celle de la lumière si le photon est effectivement de masse nulle) et
la vitesse d'un signal lumineux dans un système de coordonées fixé (en clair un système géocentrique ou héliocentrique pour
les mesures du redshift des satellites incriminés).
EN BREF PIONEER EST SOUMIS A UN CHAMP D'ACCELERATION COSMOLOGIQUE (covariant) DE L'ORDRE DE -q_o H_o^2 r et
envoie DES PHOTONS DONT L'ACCELERATION DU MOUVEMENT (non covariant) VAUT c H_o en première approximation.
En tant que mathématicien, je ne peux aller plus loin, aux astrophysiciens de trancher;
en effet "l'accélération" a_p déterminée provient de mesure de décalage spectral, donc on a tout lieu de penser
a priori que a_p traduit la variation du redshift (covariant), donc dz/d tau. Mais pour évaluer a_p,
il y a des corrections faites qui tiennent compte de la répartition de masses dans le système solaire.
Si, pour effectuer une seule de ces corrections, il est utilisé une distance spatiale (objet non covariant) alors
l'objet a_p évalué n'est pas covariant. Il se peut alors qu'il représente bien l'évolution de la distance
lumineuse de Pioneer, mesurée via des décalages spectraux (covariants) et des corrections (newtoniennes ou autres)
non covariantes. Ainsi pour moi le débat n'est pas tranché.

Note : dans les formules, la vitesse de la lumière vaut 1 (et H est l'inverse d'une longueur).
 L'Effet Pioneer et les formes de métrique de l'univers
L'Effet Pioneer et les formes de métrique de l'univers L'Effet Pioneer et les formes de métrique de l'univers
L'Effet Pioneer et les formes de métrique de l'univers
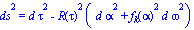
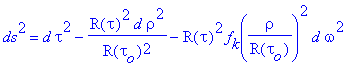
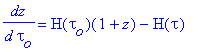
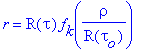 , on obtient la forme de métrique
suivante dans les coordonnées (tau,r):
, on obtient la forme de métrique
suivante dans les coordonnées (tau,r): 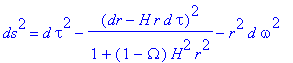
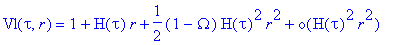
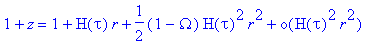
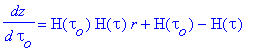
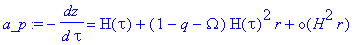
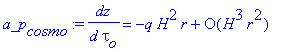
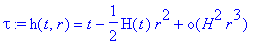
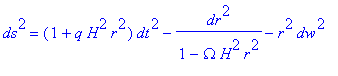
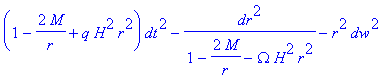
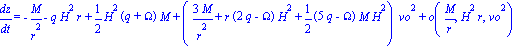

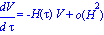 Et si ce n'était pas tout simplement cette accélération cosmologique de la "vitesse"
de la lumière qui est mise en évidence ? Cet exemple montre qu'il est important de ne pas confondre
l'invariance de la vitesse limite c, (celle de la lumière si le photon est effectivement de masse nulle) et
la vitesse d'un signal lumineux dans un système de coordonées fixé (en clair un système géocentrique ou héliocentrique pour
les mesures du redshift des satellites incriminés).
Et si ce n'était pas tout simplement cette accélération cosmologique de la "vitesse"
de la lumière qui est mise en évidence ? Cet exemple montre qu'il est important de ne pas confondre
l'invariance de la vitesse limite c, (celle de la lumière si le photon est effectivement de masse nulle) et
la vitesse d'un signal lumineux dans un système de coordonées fixé (en clair un système géocentrique ou héliocentrique pour
les mesures du redshift des satellites incriminés).
