On appelle graphe la donnée d'un ensemble de points appelés sommets et d'un ensemble de lignes appelées arêtes qui relient certains sommets entre eux.

Le nombre de sommets d'un graphe s'appelle l'ordre du graphe.

Deux sommets reliés entre eux par une arête sont dits adjacents.

Le degré d'un sommet est le nombre d'arêtes issues de ce sommet.

Un sommet qui n'est adjacent à aucun autre sommet du graphe est dit isolé.

Un graphe est dit complet si deux sommets quelconques distincts sont toujours adjacents.

Autrement dit, tous les sommets sont reliés deux à deux par une arête.

Exemple de graphes

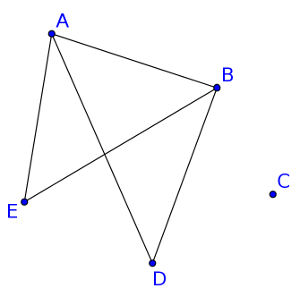	Le graphe ci-contre est d'ordre 5 car il possède 5 sommets Les sommets A et B sont adjacents Les sommets D et E ne sont pas adjacents Le sommet C est isolé
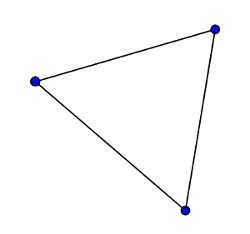	Le graphe ci-contre est complet d'ordre 3
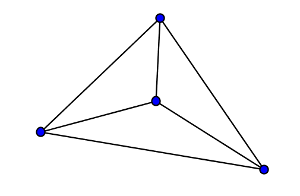	Le graphe ci-contre est complet d'ordre 4

Un graphe peut être orienté ou non-orienté.

Dans un graphe non-orienté, chaque arête peut-être parcourue dans les deux sens.

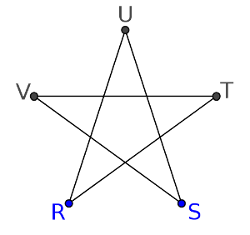
Dans un graphe orienté, chaque arête ne peut-être parcourue que dans un seul sens indiqué par une flèche.

Un graphe (orienté ou non-orienté) peut contenir des boucles c'est-à-dire une arête dont l'origine et l'extrémité correspondent au même sommet (on a par exemple une boucle B sur la représentation précédente).

On considère un graphe non orienté à \( n \) sommets. Soit \( d_i \) le degré du sommet \( i \), \( 1 \leqslant i \leqslant n \). Soit A le nombre d'arêtes du graphe.

On a \( \;\; A = \frac{1}{2} \sum\limits_{\substack{i=1}}^{n}{d_i} \)

Autrement dit, le nombre d'arêtes est égal à la moitié de la somme des degrés des sommets

Ce résultat s'explique assez facilement: en ajoutant les degrés de chaque sommet (c'est à dire le nombre d'arêtes issues de ce sommet), on comptabilise deux fois chaque arête (une fois avec le sommet d'une extrémité et une seconde fois avec le sommet de l'autre extrémité de l'arête). D'où le résultat.

Il découle de cette propriété que la somme des degrés des sommets est nécessairement paire et donc que le nombre de sommets de degré impair est pair.