Formation I.S.N.

Le parcours en largeur avec Python

Comment représenter un graphe avec Python

Nous avons vu dans la partie présentant la notion de graphe, que tout graphe est caractérisé par sa matrice d'adjacence composée de 1 et de 0 selon que deux sommets sont ou ne sont pas reliés par une arête.

Une façon d'encoder un graphe sous Python est d'utiliser un dictionnaire qui sera la représentation de sa matrice d'adjacence. La clé associée à chaque sommet sera la liste des sommets adjacents.



Prenons l'exemple de ce graphe :

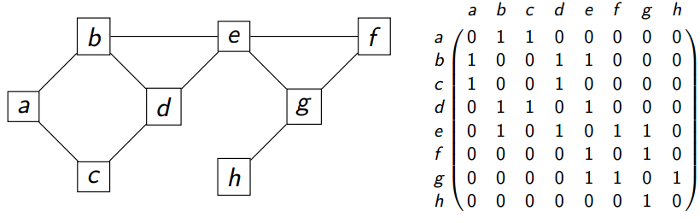
Exemple-graphe-matrice

On utilisera un dictionnaire python de la façon suivante:


G = dict()
G['a'] = ['b','c']
G['b'] = ['a','d','e']
G['c'] = ['a','d']
G['d'] = ['b','c','e']
G['e'] = ['b','d','f','g']
G['f'] = ['e','g']
G['g'] = ['e','f','h']
G['h'] = ['g']

Programmation Python du BFS (Breadth First Search)

Avec une telle représentation d'un graphe, la programmation du BFS se réalisera avec une fonction bfs(graphe, sommet de départ) dont les variables seront les suivantes :

  • Un dictionaire P tel que, en fin de parcours, pour tout sommet S du graphe, P[S] sera le père de S, c'est-à-dire le sommet à partir duquel le sommet S a été découvert lors du parcours.
  • Un dictionnaire couleur tel que, pour tout sommet S, couleur[S] soit blanc si le sommet S n'est pas passé dans la file, gris si le sommet S est dans la file et noir si le sommet S est sorti de la file.
  • Une liste Q utilisée comme file (FIFO) : on enfile un sommet lorsqu'il est découvert et on le défile lorsqu'il est terminé (traitement prioritaire des sommets découverts au plus tôt).

Voici un exemple de déroulement de la fonction avec l'appel bfs(G, 'b'):



Déroulement détaillé de la fonction bfs()
Etape 1

P = {'b' : None}

Q = ['b']

Découverts(gris ou noirs) = ['b']

Fermés(noirs) = []

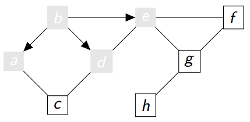Etape 2

P = {'b': None , 'a': 'b' , 'd': 'b' , 'e': 'b'}

Q = ['b', 'a', 'd', 'e']

Découverts(gris ou noirs) = ['b', 'a', 'd', 'e']

Fermés(noirs) = []

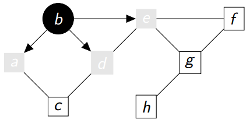Etape 3

P = {'b':None , 'a':'b' , 'd':'b' , 'e':'b'}

Q = ['a', 'd', 'e']

Découverts(gris ou noirs) = ['a', 'd', 'e']

Fermés(noirs) = ['b']

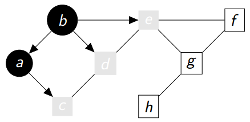Etape 4

P = {'b':None , 'a':'b' , 'd':'b' , 'e':'b' , 'c':'a'}

Q = ['d', 'e', 'c']

Découverts(gris ou noirs) = ['b', 'a', 'd', 'e', 'c']

Fermés(noirs) = ['b', 'a']

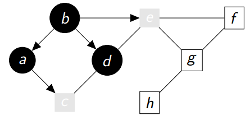Etape 5

P = {'b':None , 'a':'b' , 'd':'b' , 'e':'b' , 'c':'a'}

Q = ['e', 'c']

Découverts(gris ou noirs) = ['b', 'a', 'd', 'e', 'c']

Fermés(noirs) = ['b', 'a', 'd']

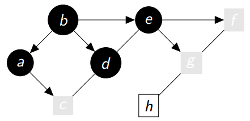Etape 6

P = {'b':None , 'a':'b' , 'd':'b' , 'e':'b' , 'c':'a' , 'f':'e' , 'g':'e'}

Q = ['c', 'f', 'g']

Découverts(gris ou noirs) = ['b', 'a', 'd', 'e', 'c', 'f', 'g']

Fermés(noirs) = ['b', 'a', 'd', 'e']

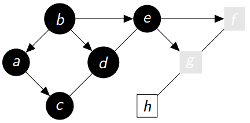Etape 7

P = {'b':None , 'a':'b' , 'd':'b' , 'e':'b' , 'c':'a' , 'f':'e' , 'g':'e'}

Q = ['f', 'g']

Découverts(gris ou noirs) = ['b', 'a', 'd', 'e', 'c', 'f', 'g']

Fermés(noirs) = ['b', 'a', 'd', 'e', 'c']

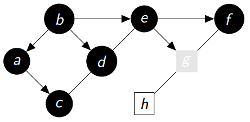Etape 8

P = {'b':None , 'a':'b' , 'd':'b' , 'e':'b' , 'c':'a' , 'f':'e' , 'g':'e'}

Q = ['g']

Découverts(gris ou noirs) = ['b', 'a', 'd', 'e', 'c', 'f', 'g']

Fermés(noirs) = ['b', 'a', 'd', 'e', 'c', 'f']

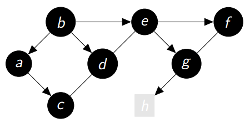Etape 9

P = {'b':None , 'a':'b' , 'd':'b' , 'e':'b' , 'c':'a , 'f':'e' , 'g':'e' , 'h':'g'}

Q = ['h']

Découverts(gris ou noirs) = ['b', 'a', 'd', 'e', 'c', 'f', 'g', 'h']

Fermés(noirs) = ['b', 'a', 'd', 'e', 'c', 'f', 'g']

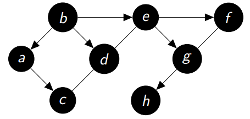Etape 10

P = {'b':None , 'a':'b' , 'd':'b' , 'e':'b' , 'c':'a' , 'f':'e' , 'g':'e' , 'h':'g'}

Q = []

Découverts(gris ou noirs) = ['b', 'a', 'd', 'e', 'c', 'f', 'g', 'h']

Fermés(noirs) = ['b', 'a', 'd', 'e', 'c', 'f', 'g', 'h']



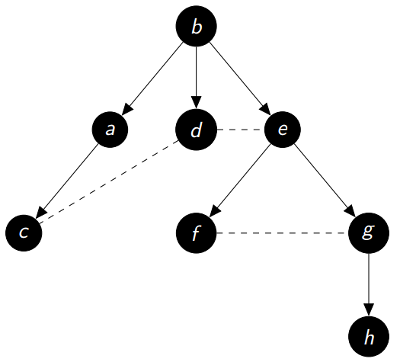
L'arborescence associée au parcours peut donc être modélisée de la façon suivante :

Arborescence

L'ordre de parcours est ligne après ligne et de gauche à droite pour chacune des lignes.

Un code Python pour la fonction bfs() pourrait donc être : 


def bfs(G, S):
	couleur = dict()
	for x in G :
		couleur[x] = 'blanc'
	P = dict()
	P[S] = None
	couleur[S] = 'gris'
	Q = [S]
	while Q :
		u = Q[0]
		for v in G[u]:
			if couleur[v] == 'blanc':
				P[v] = u
				couleur[v] = 'gris'
				Q.append(v)
		Q.pop(0)
		couleur[u] = 'noir'
	return P

fichier code

Ne gardons que l'essentiel: 


def bfs(G,s) :
	P,Q={s :None},[s]
	while Q :
		u=Q.pop(0)
		for v in G[u] :
			if v in P : continue
			P[v]=u
			Q.append(v)
	return P

fichier code

Et si l'on veut expliciter l'usage de la notion de file: 


class Maillon:

	def __init__(self, valeur, precedent=None, suivant=None):
		self.valeur = valeur
		self.precedent = precedent
		self.suivant = suivant


class File:

	def __init__(self):
		self.longueur = 0
		self.debut = None
		self.fin = None

	def enfiler(self, valeur):
		if self.longueur == 0:
			self.debut = self.fin = Maillon(valeur)
		else:
			self.fin = Maillon(valeur, self.fin)
			self.fin.precedent.suivant = self.fin
		self.longueur += 1


	def defiler(self):
		if self.longueur > 0:
			valeur = self.debut.valeur
			if self.longueur > 1:
				self.debut = self.debut.suivant
				self.debut.precedent = None
			else:
				self.debut = self.fin = None
			self.longueur -= 1
		return valeur


	def estVide(self):
		return self.longueur == 0

 




def bfs(G,s) :
	P = {s :None} 
	Q = File()
	Q.enfiler(s)
	while not(Q.estVide()) :
		u = Q.defiler()
		for v in G[u] :
			if v in P : continue
			P[v]=u
			Q.enfiler(v)
	return P



G = dict()
G['a'] = ['b','c']
G['b'] = ['a','d','e']
G['c'] = ['a','d']
G['d'] = ['b','c','e']
G['e'] = ['b','d','f','g']
G['f'] = ['e','g']
G['g'] = ['e','f','h']
G['h'] = ['g']


P = bfs(G,'b')
print(P)