Nous présenterons la preuve de la conjecture A de Bombieri,
Masser et Zannier, cas particulier de conjectures proposées
indépendamment par Zilber et Pink.
Si C est une courbe algébrique tracée sur un tore multiplicatif A= G_m^g au-dessus de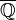
, il
s'agit de montrer la finitude de l'ensemble des points x appartenant à
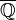C() soumis à deux équations indépendantes
de la forme x_1^{α_1}... x_g^{α_g}=1, pour
α_1,...,α_g appartenant à Z, et ceci sous
l'hypothèse minimale : C n'est contenue dans aucun sous-groupe
algébrique propre de A. En s'appuyant sur des résultats en direction du
problème
de Lehmer, le travail de Bombieri, Masser et Zannier montre qu'il suffit de
borner la
hauteur de ces points pour obtenir leur finitude. Nous expliquerons comment
conclure la
preuve en produisant une inégalité de hauteur sur C x C par
application de
l'inégalité de Vojta généralisée de Rémond.
Si C est une courbe algébrique tracée sur un tore multiplicatif A= G_m^g au-dessus de
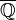, il
s'agit de montrer la finitude de l'ensemble des points x appartenant à
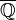C() soumis à deux équations indépendantes
de la forme x_1^{α_1}... x_g^{α_g}=1, pour
α_1,...,α_g appartenant à Z, et ceci sous
l'hypothèse minimale : C n'est contenue dans aucun sous-groupe
algébrique propre de A. En s'appuyant sur des résultats en direction du
problème
de Lehmer, le travail de Bombieri, Masser et Zannier montre qu'il suffit de
borner la
hauteur de ces points pour obtenir leur finitude. Nous expliquerons comment
conclure la
preuve en produisant une inégalité de hauteur sur C x C par
application de
l'inégalité de Vojta généralisée de Rémond.