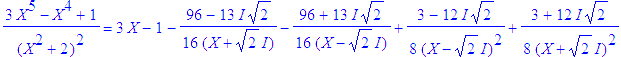Fractions rationnelles avec Maple



\(F=\dfrac{X^8\!+\!1}{X^3(X\!-\!1)^4}\)


Décomposition sur \(\mathbb{R} :\)

>    convert((X^8+1)/(X^3*(X-1)^4),parfrac);

Primitive :

>    int((x^5+2)/(x*(x+1)*(x^2+x+1)),x);




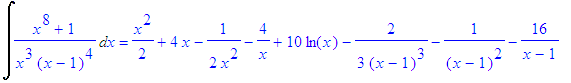
\(\begin{array}{rl}F\hspace{-0.5em}&=\dfrac{1}{(1\!-\!X)(1\!-\!X^2)}\\ &=\dfrac{1}{(1\!-\!X)^2(1\!+\!X)}\end{array}\)


Décomposition sur \(\mathbb{R} :\)

>    convert(1/((1-X)*(1-X^2)),parfrac);

Primitive :

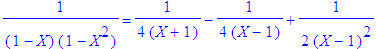
>    int(1/((1-x)*(1-x^2)),x);




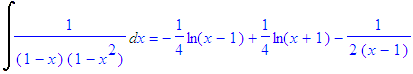
\(\begin{array}{rl}F\hspace{-0.5em}&=\dfrac{1}{(1\!-\!X)(1\!-\!X^2)(1\!-\!X^3)}\\ &=\dfrac{1}{(1\!-\!X)^3(1\!+\!X)(1\!+\!X\!+\!X^2)}\end{array}\)


Décomposition sur \(\mathbb{R} :\)

>    convert(1/((1-X)*(1-X^2)*(1-X^3)),parfrac);

Primitive :

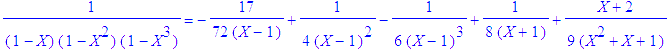
>    int(1/((1-x)*(1-x^2)),x);

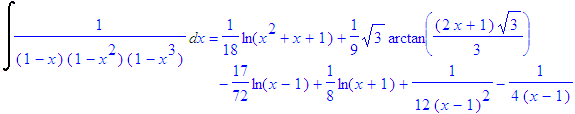
Décomposition sur \(\mathbb{C}\) (numérique) :

>    convert(1/((1-X)*(1-X^2)*(1-X^3)),parfrac,complex);


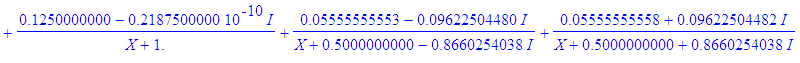
Décomposition sur \(\mathbb{C}\) (formelle) :

>    convert(1/((1-X)*(1-X^2)*(1-X^3)),parfrac,{I,sqrt(3)});


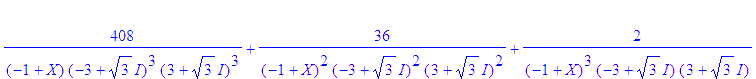
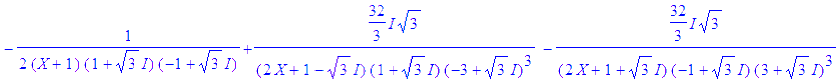
Simplification des coefficients complexes :

>    evalc(408/(-1+X)/(-3+3^(1/2)*I)^3/(3+3^(1/2)*I)^3),
evalc(36/(-1+X)^2/(-3+3^(1/2)*I)^2/(3+3^(1/2)*I)^2),
evalc(2/(-1+X)^3/(-3+3^(1/2)*I)/(3+3^(1/2)*I)),
evalc(-1/(2*(X+1)*(1+3^(1/2)*I)*(-1+3^(1/2)*I))),
evalc(9*32/3*I*3^(1/2)/(1+3^(1/2)*I)/(-3+3^(1/2)*I)^3)/9/(2*X+1-I*3^(1/2)),
evalc(-9*32/3*I*3^(1/2)/(-1+3^(1/2)*I)/(3+3^(1/2)*I)^3)/9/(2*X+1+I*3^(1/2));

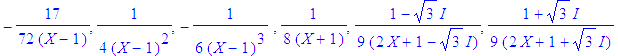
Décomposition \(\mathbb{C} :\)

>    sum(%[k],k=1..6);




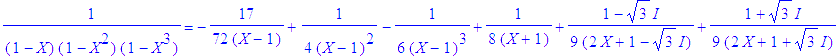
Application : un problème de dénombrement

On a d'une part :

\(\begin{array}{rl} F\hspace{-0.5em} &=\dfrac{1}{(1\!-\!X)(1\!-\!X^2)(1\!-\!X^3)}\\ &=\dfrac{1}{1\!-\!X}\!\!\times\!\!\dfrac{1}{1\!-\!X^2}\!\!\times\!\!\dfrac{1}{1\!-\!X^3}\\ &=\displaystyle\sum_{i=0}^{\infty} X^i\sum_{j=0}^{\infty} X^{2j}\sum_{k=0}^{\infty} X^{3k}\\ &=\displaystyle\sum_{(i,j,k)\in\mathbb{N}^3} X^{i+2j+3k}\\ &=\displaystyle\sum_{n=0}^{\infty}a_n X^n \end{array}\)

avec \(a_n=\mathrm{card}\{(i,j,k)\in\mathbb{N}^3:i+2j+3k=n\}.\)
L'entier \(a_n\) représente le nombre de façons de constituer la somme de \(n\) € avec des pièces de 1 €, 2 € et 3 € (avec un peu d'imagination)…


D'autre part :

\(\begin{array}{rcl} F\hspace{-0.5em} &=&\hspace{-0.5em} \dfrac{17}{72}\dfrac{1}{1\!-\!X}+\dfrac{1}{4}\dfrac{1}{(1\!-\!X)^2} +\dfrac{1}{6}\dfrac{1}{(1\!-\!X)^3}\\ &&\hspace{-0.5em} +\dfrac{1}{8}\dfrac{1}{1\!+\!X}+\dfrac{1}{9}\dfrac{1}{1\!-\mathrm{e}^{\mathrm{i}2\pi/3}\!X} +\dfrac{1}{9}\dfrac{1}{1\!-\mathrm{e}^{-\mathrm{i}2\pi/3}\!X}\\ &=&\hspace{-0.5em} \displaystyle\dfrac{17}{72}\sum_{n=0}^{\infty} X^n +\dfrac{1}{4}\sum_{n=0}^{\infty} (n+1)X^n+\dfrac{1}{12}\sum_{n=0}^{\infty} (n+2)(n+1)X^n\\ &&\hspace{-0.5em} \displaystyle+\dfrac{1}{8}\sum_{n=0}^{\infty} (-1)^nX^n +\dfrac{1}{9}\sum_{n=0}^{\infty} \mathrm{e}^{\mathrm{i}2n\pi/3}X^n +\dfrac{1}{9}\sum_{n=0}^{\infty} \mathrm{e}^{-\mathrm{i}2n\pi/3}X^n \end{array}\)



Par identification, on en tire :

\(a_n=\dfrac{1}{12}n^2+\dfrac{1}{2}n+\dfrac{47}{72}+\dfrac{1}{8}(-1)^n+\dfrac{2}{9}\cos\left(\dfrac{2n\pi}{3}\right)\)



>    series(1/((1-X)*(1-X^2)*(1-X^3)),X=0,20);





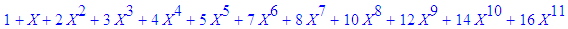
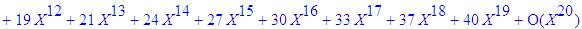
\(F=\dfrac{X\!-\!2}{(X \!-\! 1)(X\!+\!1)(X^2\!+\!3)^2}\)


Décomposition sur \(\mathbb{R} :\)

>    convert((X-2)/((X-1)*(X+1)*(X^2+3)^2),parfrac);

Primitive :

>    int(1/((1-x)*(1-x^2)),x);

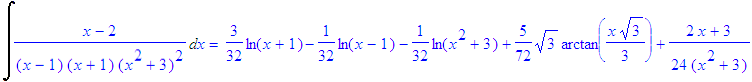
Décomposition sur \(\mathbb{C}\) (numérique) :

>    convert((X-2)/((X-1)*(X+1)*(X^2+3)^2),parfrac,complex);


Décomposition \(\mathbb{C} :\)

>    convert((X-2)/((X-1)*(X+1)*(X^2+3)^2),parfrac,{I,sqrt(3)});



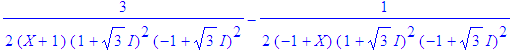
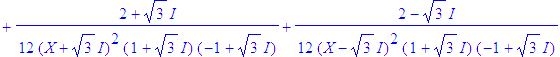
Simplification des coefficients complexes :

>    evalc(48/12*(2+3^(1/2)*I)/(1+3^(1/2)*I)/(-1+3^(1/2)*I))/48/(X+3^(1/2)*I)^2,
evalc(48/12*(2-I*3^(1/2))/(1+3^(1/2)*I)/(-1+3^(1/2)*I))/48/(X-I*3^(1/2))^2,
evalc(3/2/(X+1)/(1+3^(1/2)*I)^2/(-1+3^(1/2)*I)^2),
evalc(-1/(2*(-1+X)*(1+3^(1/2)*I)^2*(-1+3^(1/2)*I)^2)),
evalc(288/18*(10*I*3^(1/2)-9)/(1+3^(1/2)*I)^2/(-1+3^(1/2)*I)^2)/288/(X+3^(1/2)*I),
evalc(288/18*(-10*I*3^(1/2)-9)/(1+3^(1/2)*I)^2/(-1+3^(1/2)*I)^2)/288/(X-I*3^(1/2));  #simplification forcée des complexes

Décomposition \(\mathbb{C} :\)

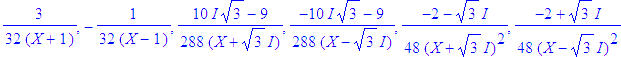
>    sum(%[k],k=1..6)




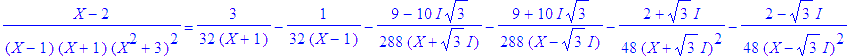
\(F=\dfrac{3X^5\!-\!X^4\!+\!1}{(X^2\!+\!2)^2}\)


Décomposition sur \(\mathbb{R} :\)

>    convert((3*X^5-X^4+1)/(X^2+2)^2,parfrac);

Primitive :

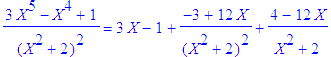
>    int(1/((1-x)*(1-x^2)),x);

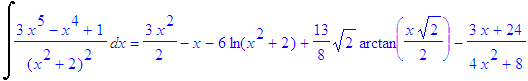
Décomposition sur \(\mathbb{C}\) (numérique) :

>    convert((3*X^5-X^4+1)/(X^2+2)^2,parfrac,complex);

Décomposition sur \(\mathbb{C} :\)

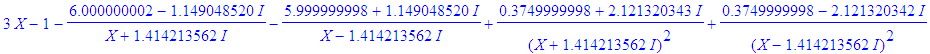
>    convert((3*X^5-X^4+1)/(X^2+2)^2,parfrac,{I,sqrt(2)});