This tutorial dates few years back, it might not be fully up-to-date, but the main interface and commands are the same.
Matlab has several tutorials (in English) that you can find here https://fr.mathworks.com/help/matlab/getting-started-with-matlab.html.
elements de l'interface graphique
la fenetre matlab est divisee en plusieurs espaces qui peuvent etre configurés. l'espace le plus important est la command windows. cette fenetre permet d'executer des commandes matlab. l'autre espace important est l'editeur de texte, qui vous permet d'editer des fichier qui pourront etre executes par matlab.
Philosophie
Matlab, qui est l'abbreviation de MATrix LABoratory, est optimisé pour manipuler des matrices. Pour en tirer parti, il faut vectorialiser les expressions. En C, pour initialiser un vecteur x qui prendra les valeurs de 1 a 1000000 (un million), on procéderait de la façon suivante:
double *x;
int i, sizex = 1000000;
x = malloc(size*sizeof(double));
for ( i = 0; i < sizex; i++)
{
x[i] = i+1.0;
}
Sous Matlab, la meme procedure se fait de la facon suivante:
x = 1:1000000;L'initialisation est vectorialisée: le membre de droite (
1:1000000) est le vecteur 1 à 1000000 et l'assignation se fait de vecteur à vecteur.
Notez qu'il n'est pas nécessaire de déclarer la variable x, elle est créée lors de l'initialization. Le type (en Matlab la class) sera automatiquement un array de double:
class(x)
ans = double
Contrairement à C, les expressions n'ont pas à se terminer par un ;. Si le ; est omis, le résultat de l'expression sera affiché dans la Command Windows. L'expression
1+1;ne produit aucun effet (mais le résultat est stocké dans une variable appelée
ans). L'expression
1+1
ans = 2renvoie le resultat escompté: 2.
Les valeurs scalaires sont des arrays 1x1, et ne sont pas different des arrays représentant des vecteurs ou des matrices.
On aurait pu initialiser x comme en C, mais cela aurait été beaucoup plus long. Les commandes tic et toc permettent de calculer un intervalle de temps écoulé:
clearvars x; % on efface la variable x tic x = 1:1000000; toc
Elapsed time is 0.003285 seconds.
Maintenant, avec la boucle for:
clearvars x;
tic
for i = 1:1000000
x(i) = i;
end
toc
Elapsed time is 0.573735 seconds.
La boucle for est beaucoup plus lente que l'assignation vectorielle! Conclusion, si on peut, on evite les boucles for en Matlab.
Variables, vecteurs, matrices
La type de variable de base de Matlab est l'array de double. Il existe d'autres types (class en Matlab) comme les char, cell, struct, int8, etc, mais les double sont utilisés la plupart du temps. Comme les variables créées sont de classe double par défaut, on suppose qu'on travaillera en double dans ce tutoriel. Un array de double A peut comporter plusieurs dimensions. Pour un array de dimension 2, c.-à-d. un matrice (le défaut), on accède au coefficient de la ligne i, colonne j par A(i,j). (Comparer à C: A[i-1][j-1].)
Voici un liste de commandes pour créer des vecteurs (mx1 pour un vecteur colonne, et 1xn pour un vecteur ligne).
m = 10; n = 10; xcol = ones(m,1); % cree un vecteur colonne de dimension 10 avec UNs partout xline = ones(1,n); % cree un vecteur ligne de dimension 10 avec UNs partout ycol = (1:m)'; % cree un vecteur colonne des entiers de 1 a m. Le ' est l'adjoint yline = 1:n; % cree un vecteur ligne des entiers de 1 a n. z1 = linspace(0,1,n); % cree le vecteur ligne des n doubles espaces lineairement entre 0 et 1. h = 1/(n-1); % definit la distance entre deux elements de z1 z2 = 0:h:1; % autre facon de definir le meme vecteur, mais attention aux erreurs d'arrondis!
isequal(z1,z2) % on teste pour savoir si |z1 == z2|, le resultat est FAUX.
ans =
0
pour connaitre les dimensions des variables xcol et xline, on peut utiliser les commandes length et size. La commande size renvoie la taille de chaque dimension
size(xcol) size(xline)
ans =
10 1
ans =
1 10
La commande length renvoie la plus grande taille seulement, ce qui est pratique pour des expressions du type
mcols = length(xcol);
L'autre facon de connaitre l'état des variables est la commande whos
whos
Name Size Bytes Class Attributes ans 1x2 16 double h 1x1 8 double i 1x1 8 double m 1x1 8 double n 1x1 8 double x 1x1000000 8000000 double xcol 10x1 80 double xline 1x10 80 double ycol 10x1 80 double yline 1x10 80 double z1 1x10 80 double z2 1x10 80 double
Cette commande affiche toutes les variables du workspace courant. Le workspace contient les variables définies par l'utilisateur.
De la même façon que les vecteurs, on peut créer des matrices mxn.
A = ones(m,n); % cree une matrice 10x10 avec UNs partout Ar = rand(m,n); % cree une matrice 10x10 avec nombres pseudo-aleatoires entre 0 et 1 A = vander(z1); % cree une matrice carree de Vandermonde de taille length(z1)
Aide
Pour de l'aide sur une commande, tapez help nom_de_la_commande
Par exemple, pour afficher l'aide sur la commande ones:
help ones
ONES Ones array.
ONES(N) is an N-by-N matrix of ones.
ONES(M,N) or ONES([M,N]) is an M-by-N matrix of ones.
ONES(M,N,P,...) or ONES([M N P ...]) is an M-by-N-by-P-by-... array of
ones.
ONES(SIZE(A)) is the same size as A and all ones.
ONES with no arguments is the scalar 1.
ONES(..., CLASSNAME) is an array of ones of class specified by CLASSNAME.
Note: The size inputs M, N, and P... should be nonnegative integers.
Negative integers are treated as 0.
Example:
x = ones(2,3,'int8');
See also EYE, ZEROS.
Overloaded methods:
distributed/ones
codistributor2dbc/ones
codistributor1d/ones
codistributed/ones
gpuArray/ones
Reference page in Help browser
doc ones
La ligne See also est utile pour trouver des commandes similaire. Ici on trouve les commandes zeros et eye qui permettent d'initialiser des matrices (ou vecteurs) de zeros et la matrice identité. Si vous ne comprenez pas ce que Matlab vous affiche, vous pouvez essayer la commande why.
Principales commandes et syntaxe sur les vecteurs et matrices
a = 2.0 % assigne la valeur 2 a la variable a (a == 2) % teste l'egalite entre 2 et a find(x == 200) % trouve coefficients i verifiant l'expression logique x(i) == 200 find(x < 10) % trouve coefficients i verifiant l'expression logique x(i) < 10 A*xcol % multiplication matrice*vecteur colonne xline*A % multiplication vecteur ligne*matrice A\x % division a gauche (calcule A^(-1)*x) A(:,1:2:end) % colonnes impaires de A A([1 2 5 6],:) % lignes 1, 2, 5, et 6
Fonctions et scripts
Les fonctions Matlab sont le plus souvent ecrites dans un fichier texte séparé. Le nom du fichier est le nom de la fonction. La fonction du fichier mafonction.m sera donc appelée par Matlab par la commande mafonction. Construisons un fonction qui prend en argument deux vecteurs de même taille, x et y, et qui renvoie les coefficients du polynôme de degré n qui interpole au sens des moindres carres y aux points x: y ~ p(x).
edit monpolyfit.m
La premiere ligne du fichier monpolyfit.m doit etre
function p = monpolyfit(x,y,n)
Le mot cle function indique que le fichier est une fonction. p est la la variable retournee par la fonction et (x,y,n) sont les arguments de la fonction. La notation function [p1, p2] = mafonction(x,y) est utilisee s'il y a plusieurs variables de sortie et function mafunction(x,y) est utilisee si il n'y a pas de variable de sortie (pour une fonction qui genererait un graphique ou un fichier, par exemple).
La deuxieme ligne devrait etre un ligne descriptive de la fonction, et est en commentaire (tout le texte qui suit % jusqu'à la fin de la ligne est en commentaire):
% MONPOLYFIT interpolation polynomiale par moindres carres
Cette ligne est utilisée pour afficher les descriptions courtes des fonction lorque, par exemple la commande lookfor est utilisée. Les lignes suivantes, en commentaire, décrivent l'usage de la fonction. C'est le moment de mettre le See also, pour faire un lien vers d'autres fonctions Matlab. Ici on pourrait faire un lien vers la fonction polyfit de Matlab.
% See also POLYFIT
(Les majuscules ne se verront pas avec la commande help).
Ensuite vient le corps de la fonction. Tout d'abord on vérifie que les deux vecteurs x et y sont des vecteurs de même taille, et que n+1 est inférieur ou égal à la taille de y.
sx = size(x);
sy = size(y);
if min(sx)>1 % alors pas un vecteur
error('monpolyfit:tailledonnees','X n''est pas un vecteur');
end
if min(sy)>1 % alors pas un vecteur
error('monpolyfit:tailledonnees','Y n''est pas un vecteur');
end
if sx(2) ~= 1 % alors pas un vecteur colonne (~= : pas egal)
x = x.';% on transpose (pas conjugue)
sx = size(x); % on recalcule la taille de x
end
if sy(2) ~= 1 % alors pas un vecteur colonne (~= : pas egal)
y = y.'; % on transpose (pas conjugue)
sy = size(y); % on recalcule la taille de y
end
if (sx(1)~=sy(1)) % verifions les tailles de X et Y
error('monpolyfit:tailledonnees','Les tailles de X et Y ne correspondent pas');
end
if (n+1)>length(x)
error('monpolyfit:tailledonnees','Le degre n du polynome a ajuster est trop eleve, il doit etre inferieur a la longueur de X');
end
Maintenant on etablit notre équation normale pour les moindres carrés. On génère un matrice de Vandermonde A à l'aide de x:
A = vander(x);
A est une matrice de taille length(x). On ne retient de la matrice que les n+1 dernieres colonnes
m = sx(1); A = A(:,(m-n):m);
On cherche les coefficients du polynôme p qui approximent le mieux A*p=y. L'équation normale (en notation Matlab) est A'*A*p = A'*y. Si on fait une décomposition QR de la matrice A, on obtient l'equation R*p = Q'*y. On résoud ces equations à l'aide des fonctions householder, Qadj et backsubs.
[W,R]=householder(A); Qy = Qadjb(W,y); p = backsubs(R(1:(n+1),1:(n+1)),Qy(1:(n+1)));
Le code est termine, pas besoin de terminer le fichier avec un return ou un end. Le vecteur p est a été défini et sera retourné par la fonction. Toutes les variables créées dans la fonction sont locales à cette fonction et ne peuvent être vues à l'exterieur de celle-ci. Les variables sont détruites lors du retour de la fonction, à moins de declarer ces variables persistent. Cela pourrait etre utile, par exemple si on voulait faire plusieurs interpolations de même degre avec le même vecteur x. Il serait alors plus efficace de ne pas recalculer A et sa décomposition à chaque appel de la fonction.
Pour resoudre un problème, il est utile d'écrire dans un fichier la liste des commandes à faire. Ce fichier n'est qu'une liste d'expressions à evaluer par Matlab. Tout fichier avec l'extension .m dans le chemin de Matlab peut etre appelé de l'invite de commande. Un fichier .m est un fichier script s'il ne commence pas par function. Les fichiers script sont executés ligne par ligne et les variables sont dans le workspace.
On crée un fichier script appelé fit_polynome.m
edit fit_polynome.m
La premiere ligne devrait être une description du fichier en commentaire:
%% fit_polynome: script pour ajuster un polynome à des données
Ensuite on définit les vecteur x et y.
x = 10*rand(34,1); % 34 points aleatoires dans l'intervalle [0, 10]; y = 10*rand(34,1) + x; % 34 points aleatoires correles avec x n = 3; % interpolation avec un polynome de degre 3 p = monpolyfit(x,y,n); % on trouve le polynome qui s'ajuste le mieux
En exécutant le script fit_polynome, on obtient le polynôme p demandé. Toutes les variables définies dans le script se retrouvent dans le workspace.
Graphiques
Matlab possède plusieurs commandes pour visualiser des données. Pour tracer des donnes en 2D, on utilise la commande plot. Rajoutons dans le fichier script fit_polynome les commandes pour visualiser les nuages de points (x,y) et le graphe du polynôme p.
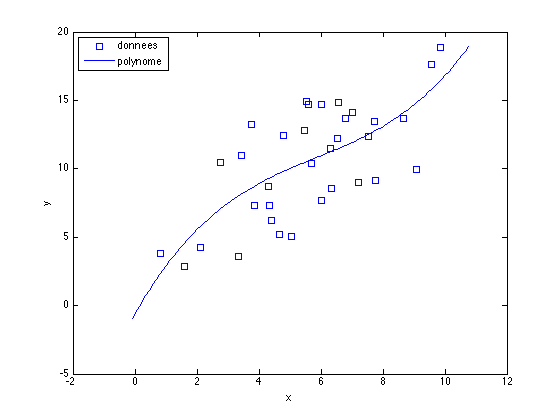
%% Visualisation 2D des donnees figure(1); % cree ou active la figure 1 clf; % clf efface la figure plot(x,y,'s') % trace les points avec des carres ('s' pour square) hold on % les prochains appels a plot n'effaceront pas les autres r = max(x)-min(x); % l'etendue de x a = min(x) - 0.1*r; % limite inferieure sur x pour tracer le polyome b = max(x) + 0.1*r; % limite superieure sur x pour tracer le polyome xp = linspace(a,b,100); % 100 points equirepartis sur [a,b] plot(xp,polyval(p,xp)) % trace le graphe de p aux valeurs xp xlabel('x') % etiquette abscisse ylabel('y') % etiquette ordonnees legend('donnees','polynome') % legende, les etiquettes sont dans % l'ordre d'aparition des plots
Pour voir le résultat, on exécute le script, fit_polynome
Resoudre un systeme d'equations differentielles ordinaires
Matlab possède plusieurs solveurs EDO, dont une suite edo*. Le solveur multi-usage à utiliser par défault est ode45 (prononcé ode quatre cinq), un solveur Runge-Kutta avec pas de temps adaptatif d'ordre 4 et 5. Les autres solveurs utiles sont ode23 et ode15s. Tous les solveurs ont la meme syntaxe:
[t,x] = ode45(@monedo,[t0 tfinal],CI); sol = ode45(@monedo,[t0 tfinal],CI);
La premiere syntaxe renvoie la solution x au temps t. La deuxieme syntaxe renvoie une structure sol qui contient la solution ainsi que des informations sur le solveur utilisé. La fonction monedo est une fonction Matlab qui définit le systeme d'EDO. Le systeme est integré sur l'intervalle [t0 tfinal], avec conditions initiales CI. L'equation différentielle est de la forme
$$\frac{dx}{dt}(t) = F(t,x).$$
avec $x(t)$ un vecteur de taille $n$. La fonction EDO doit suivre une structure bien definie, avec une premiere ligne
function dxdt = monedo(t,x)
La fonction prend en argument le temps t et l'état du systeme x. La variable x est un vecteur colonne de taille n. La fonction retourne la derivee de x au temps t dans dxdt un vecteur colonne de taille n. Les conditions initiales sont un vecteur de la meme dimension que x. Comme premier exemple, on prend le systeme de Lotka-Volterra. La fonction lotkavolterra.m spécifie le système suivant:
$$\frac{dx}{dt} = x (a - b y),$$
$$\frac{dy}{dt} = -y (c - d x).$$
Le systeme est résolu de la facon suivante:
CI = [30; 2]; tspan = [0 20]; sol = ode45(@lotkavolterra,tspan,CI);
On trace la solution à l'aide de deval, qui permet d'evaluer la solution sol à n'importe quel temps.
xint = linspace(0,20,200); yint = deval(sol,xint); figure(2); clf; plot(xint,yint) xlabel('temps'); ylabel('population');

Dans cet exemple, il n'est pas possible de facilement changer les parametres du systeme, qui sont codés dans le fichier lotkavolterra.m. De plus, pour chaque résolution du systeme, il faut définir les conditions initiales et l'intervalle d'intégration. Un fichier script peut aider, mais ne permet pas d'acceder aux paramètres, qui sont des variables locales à lotkavolterra. Un moyen de s'en sortir est d'utiliser une fonction imbriquée. Une fonction imbriquée est une sous-fonction, mais qui partage certaines variables avec la fonction principale dans laquelle elle se trouve.
A lieu de definir un script pour résoudre le systeme d'EDO, on définit une fonction run_lotka.m
function sol = run_lotka()
% RUN_LOTKA simulation du systeme de Lotka-Volterra
% parametres d'integration
CI = [30; 2];
tspan = [0 20];
% parametres du systeme
pars = [0.1 1 2 ]; % Les variables a, b, c, d sont partagees
b = 0.01; % avec la fonction imbriquee lotka
c = 1;
d = 0.02;
% resolution du systeme pour 3 jeux de parametres differents
for i = 1:3
a = pars(i); % on met a jour la valeur de a
sol{i} = ode23(@lotka,tspan,CI);
end
% plot des 3 solutions
nx = 200;
xint = linspace(tspan(1),tspan(2),nx);
figure(2); clf;
newplot; % met en place un nouveau plot
hold on % qui ne s'effacera pas a chaque appel de plot
cols = 'kbr' % couleurs k: noir, b: bleu, r:rouge
for i = 1:3
yint = deval(sol{i},xint);
plot(xint,yint,'Color',cols(i))
end
xlabel('temps'); ylabel('population');
function dxdt = lotka(~,xx) % fonction imbriquee
% LOTKA systeme d'EDO
x = xx(1); y = xx(2);
dxdt = [ x * (a - b * y)
-y * (c - d * x)];
end % on termine d'abord la fonction imbriquee
end % on termine ensuite la fonction principale
De cette facon, on peut résoudre le systeme pour n'importe quelle condition initiale, intervalle de temps et parametres du système. Le fichier run_lotka.m peut etre lancé:
run_lotka;

Codes
Les fichiers matlab peuvent etre téléchargés ici: householder.m, Qadjb.m, backsubs.m, lotkavolterra.m, run_lotka.m
La démo entière peut être téléchargée ici: tutorielmatlab.m. Ce fichier est un fichier script, qui peut exécuté par la commande tutorielmatlab, mais vous pouvez aussi l'exécuter en mode démo avec la commande echodemo tutorielmatlab. Assurez-vous d'avoir tous les fichiers nécessaires dans votre répertoire courant.