The library FELiScE
The library FELiScE is a finite element library developed at Inria in the teams REO (Paris-Rocquencourt) and MACS (Saclay). This is a parallel code (MPI) written in C++ that uses the library PETSc. In the REO team, we developed it to solve, in particular, fluid dynamics problems, electrophysiology problems or fluid-structure interaction problems. Different methods are implemented in FELiScE for fluid-structure interactions. The one we are interested in here is the Nitsche-XFEM method that we use to simulate the interaction between a fluid and an immersed interface.
The Nitsche-XFEM method
The Nitsche-XFEM method is a fictitious domain method that is able to well-capture strong discontinuities (pressure) or weak ones (fluid velocity) while not suffering from loss of accuracy. Thanks to the fictitious domain method, the fluid and interface meshes are not fitted and are fixed. Large displacement can be simulated without having to deal with deformations or remeshing of the fluid mesh. The fictitious domain is given by the XFEM part of the method that duplicates the fluid mesh elements intersected by the interface. The coupling relation between the fluid and solid equations are enforced accurately with a Nitsche’s formulation.
Thanks to this method, we can use P1/P1 finite element for the fluid problem and still capture discontinuities across the interface in both the pressure and the derivatives of the fluid velocity. The implementation of the Nitsche-XFEM method in FELiScE is interfaced with a mesh intersection algorithm developed by Frédéric Alauzet that gives all the information about the intersection between the fluid fixed mesh and the solid mesh. In particular, it is used in the two main key implementation points of the method:
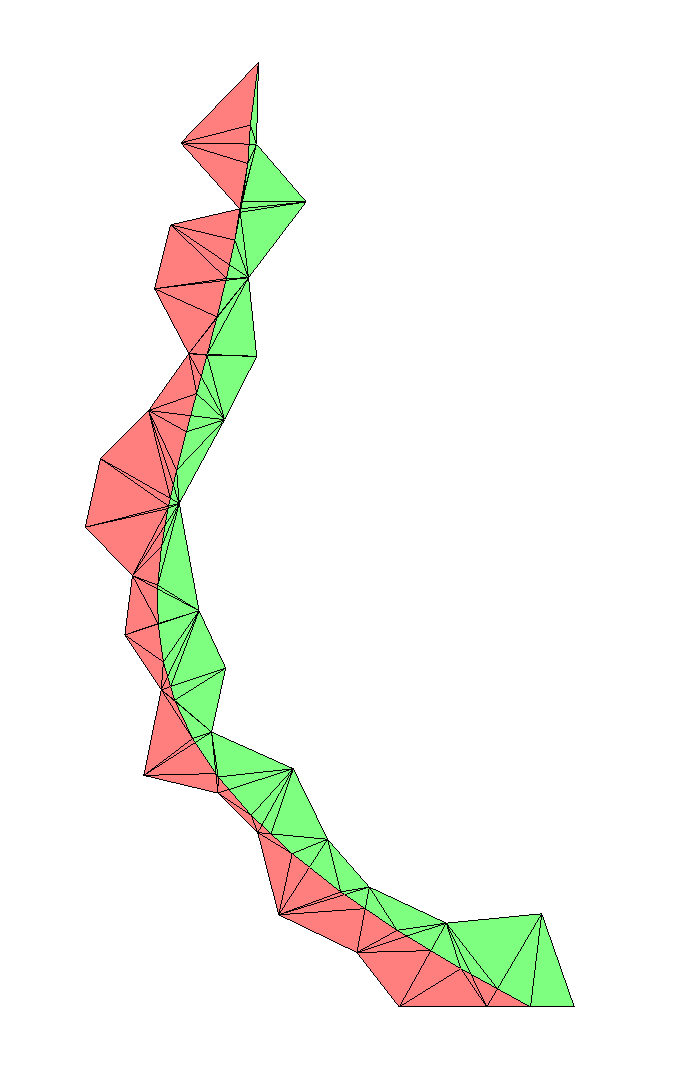
- Integration over cut-elements. The Nitsche’s formulation requires integration in the physical domain only, which is done by integrating a sub-triangulation of each intersected element. One should note that this mesh intersection is not a remeshing of the fluid mesh but only a sub-triangulation used to compute these integrals in the physical domain. The mesh resulting from the mesh intersection algorithm contains some very small and stretched elements that are not suited to run finite element computation but that are perfectly fine to only compute integrals.
- The XFEM method. The degrees of freedom of the fluid mesh elements intersected by the interface are duplicated in order to be able to capture discontinuities. The implementation in FELiScE is general enough to manage the case of an interface not cutting entirely the fluid mesh. In this case, a special treatment is done in the elements containing the tips of the interface. The solution defined in the whole domain (physical + fictitious) is saved so that one can see the smooth extension of the exact solution within the fictitious domain computed with the Nitsche’s formulation. In particular, one can note the pressure discontinuities aswell as the discontinuities in the fluid velocity derivatives. It is clear with the velocity elevations that the discontinuities are not fitted to the fluid mesh.
The pressure is double valued in the triangle intersected by the interfaces.
Note the jump in the derivatives across the interfaces. The velocity in the physical domain is smoothly extended to the fictitious domain.
Note the jump in the derivatives across the interfaces. The velocity in the physical domain is smoothly extended to the fictitious domain.
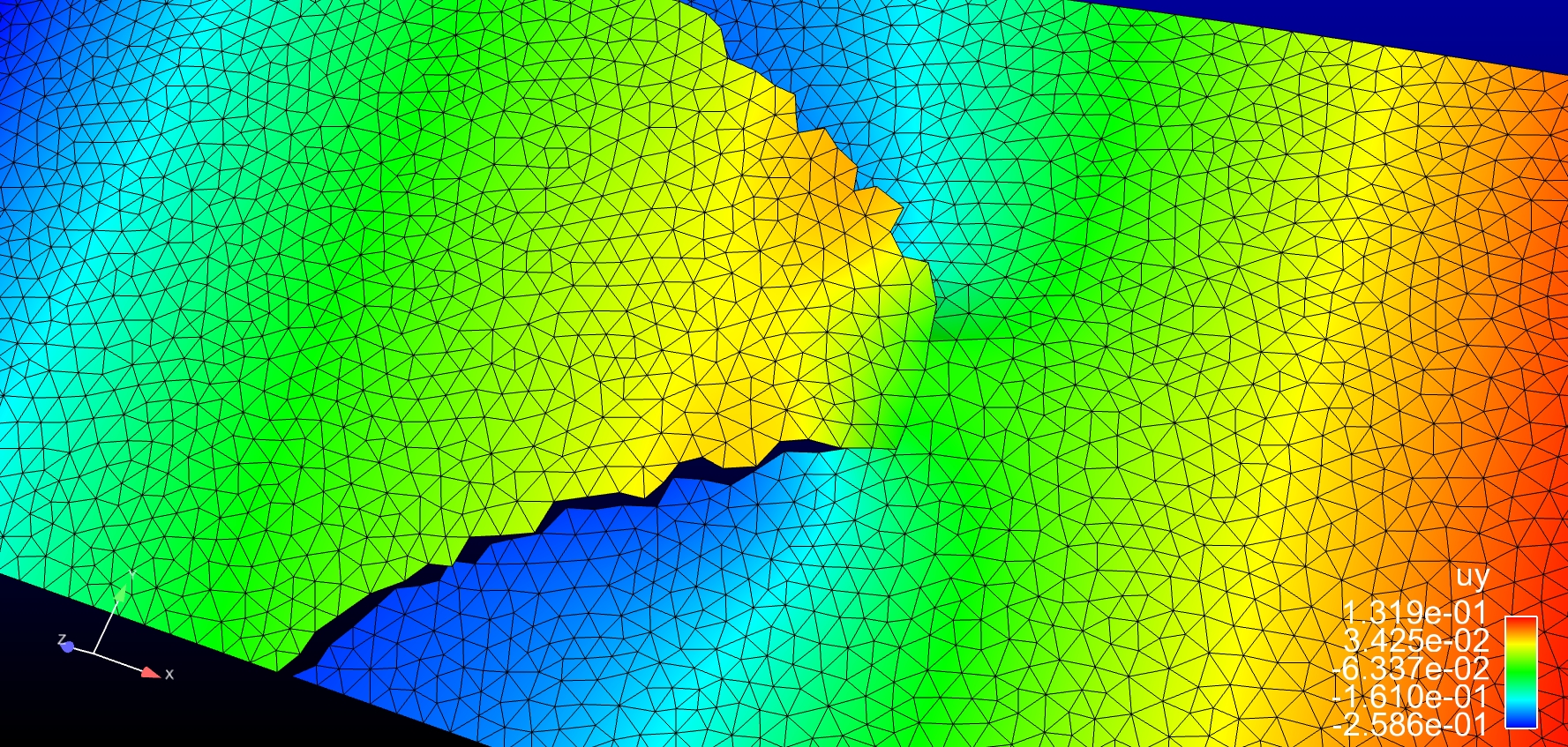
Pressure elevation
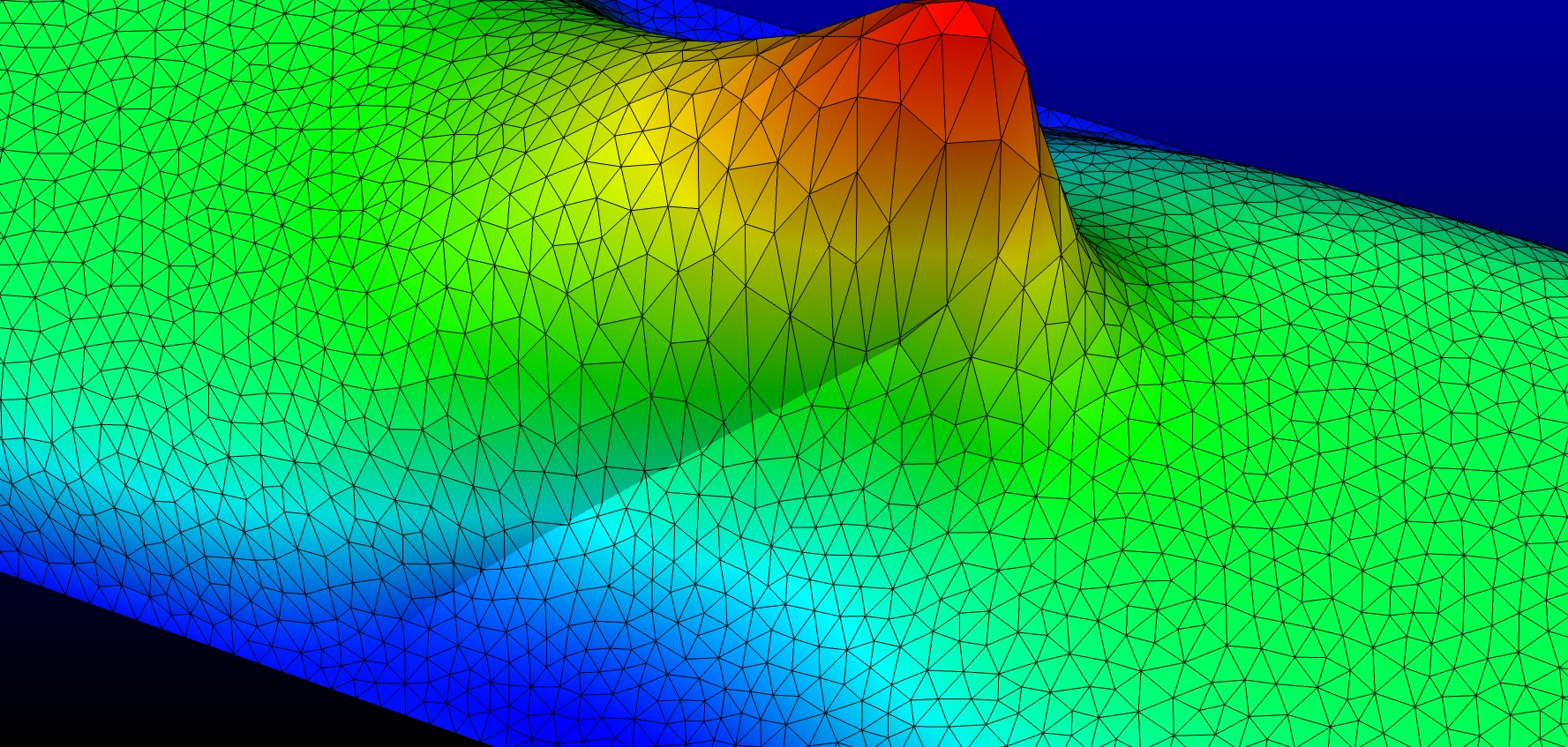
Horizontal velocity elevation
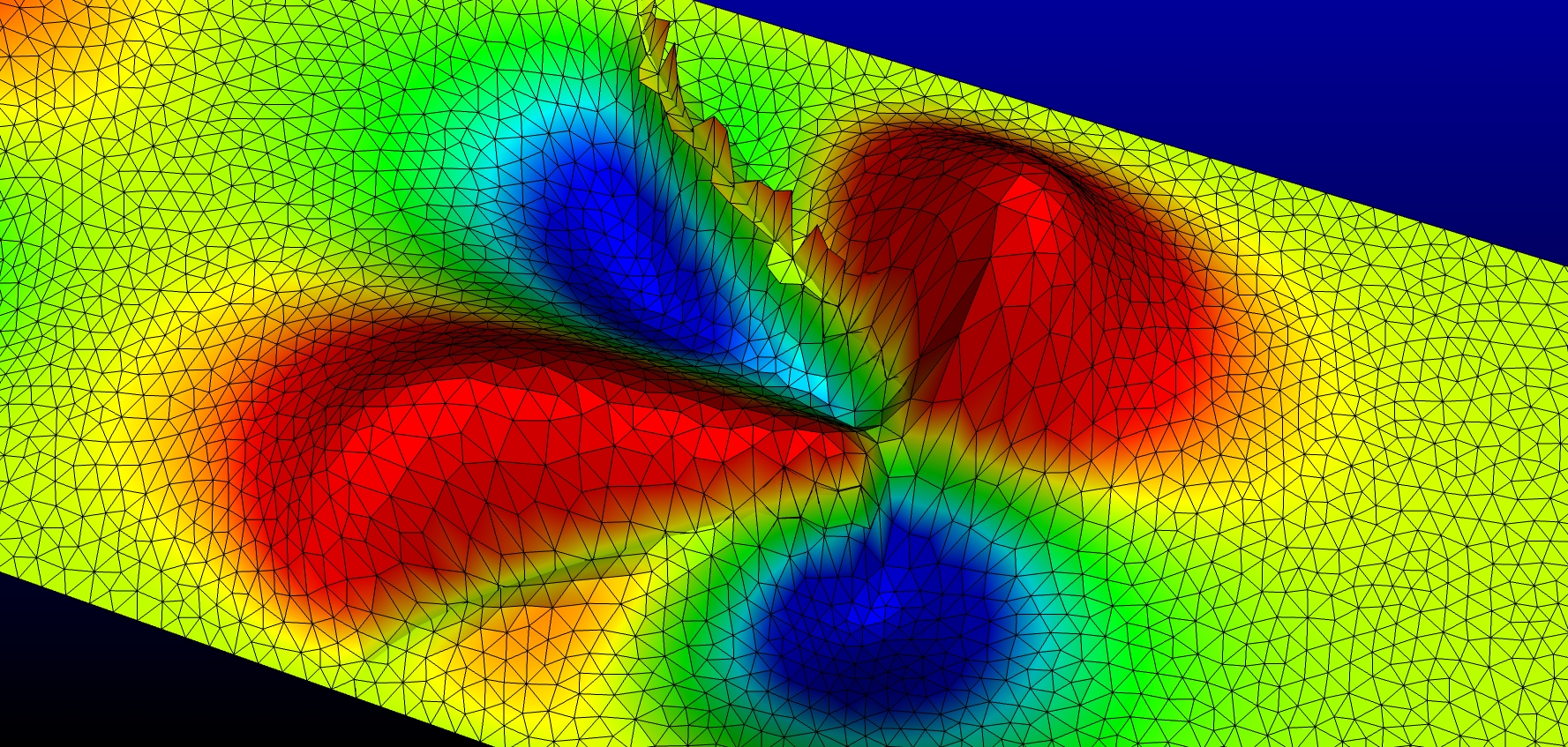
Vertical velocity elevation
The implementation is also flexible. Solid models can be plugged to the Nitsche-XFEM methods easily. Indeed, the class implementing the solid problem in the Nitsche-XFEM method is a kind of decorator whose only aim is to add the specific terms coming from the Nitsche-XFEM formulation. The solid model does not need to be known.
Some simulations
| Description | Video |
|---|---|
| A double pressure-wave (fluid from each side of the interface). A sine pressure is imposed on only one side of the interface and then vanishes to let the pressure wave evolve. An elevation of the pressure is represented. One can note the discontinuity in the pressure. A simple elastic string model is used for the interface. | |
| Here, the interface is not cutting the fluid domain in two. There are two valves with no contact and the velocity of the fluid is imposed on the left boundary. Up is the fluid velocity field and bottom is an elevation of the pressure. A linear curved beam model is used for the interfaces. | |
| This is a preliminary result, the parameter are not reflecting any physical experiment. A bubble is entering a canal and deforms. The solid model is again a linear curved beam model and the fluid inside the bubble is the same as the one outside. |
Additional information
Related documents:
- F. Alauzet, B. Fabrèges, M. A. Fernandez and M. Landajuela, Nitsche-XFEM for the coupling of an incompressible fluid with immersed thin-walled structures, Comput. Method Appl. M., 2016.