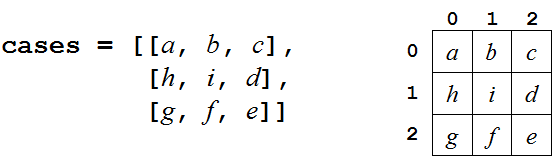On rappelle qu'avant de concevoir une interface graphique, il est nécessaire
d'avoir des algorithmes fonctionnels. Nous allons donc nous servir du
programme que vous avez réalisé pour aujourd'hui afin de concevoir
l'interface graphique d'un jeu de morpion fonctionnel.
Si vous n'avez pas réussi à concevoir un programme fonctionnel, le
paragraphe suivant vous en propose un. Toutefois, il est conseillé
de développer l'interface graphique à partir de votre propre programme si vous
avez réussi à le concevoir.
Simuler la grille
Chaque case de la grille doit être représentée par une variable.
La représentation la plus efficace est d'utiliser un tableau (liste de
listes) affecté à la variable cases. cases
est une liste de lignes, chaque ligne est une liste des cases qu'elle contient :
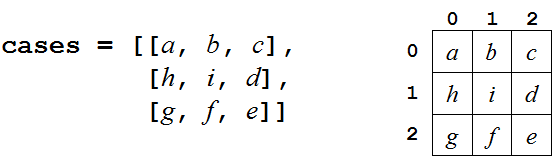
On définit cette variable globale en la remplissant de zéros :
##----- Définition des Variables globales -----##
cases = [[0, 0, 0],
[0, 0, 0],
[0, 0, 0]]
Variables globales
On définit les autres variables globales indispensables au jeu :
joueur = 1 # On commence par J1. J2 est associé au nombre -1
n = 1 # Numéro du tour de jeu
somme = 0 # Somme des cases/numéro du joueur gagnant
Visualisation en mode console
On définit une fonction d'affichage de tableau à l'écran :
##----- Définition des Fonctions -----##
def affichage(tableau):
"""Cette fonction affiche à l'écran chaque ligne d'un tableau."""
n = len(tableau)
for i in range(n) :
print(tableau[i])
Interaction
On définit une fonction qui demande la case dans laquelle jouer :
##----- Définition des Fonctions -----##
def demande(numero):
"""Cette fonction renvoie la case dans laquelle le joueur joue."""
if numero == 1:
print('Au tour du joueur n°1')
else:
print('Au tour du joueur n°2')
ligne = int(input('Numéro de ligne ?'))
colonne = int(input('Numéro de colonne ?'))
return ligne, colonne
Alignement
On définit une fonction qui vérifie l'alignement :
##----- Définition des Fonctions -----##
def verif(tableau):
"""Calcule des sommes de chaque ligne/colonne/diagonale pour
vérifier l'alignement. Elle renvoie le n° du gagnant."""
sommes = [0,0,0,0,0,0,0,0] # Il y a 8 sommes à vérifier
# Les lignes :
sommes[0] = sum(tableau[0])
sommes[1] = sum(tableau[1])
sommes[2] = sum(tableau[2])
# Les colonnes
sommes[3] = tableau[0][0]+tableau[1][0]+tableau[2][0]
sommes[4] = tableau[0][1]+tableau[1][1]+tableau[2][1]
sommes[5] = tableau[0][2]+tableau[1][2]+tableau[2][2]
# Les diagonales
sommes[6] = tableau[0][0]+tableau[1][1]+tableau[2][2]
sommes[7] = tableau[0][2]+tableau[1][1]+tableau[2][0]
for i in range(8): # Parcours des sommes
if sommes[i] == 3:
return 1
elif sommes[i] == -3:
return -1
return 0
Finalisation
On termine par la partie principale du programme :
##----- Programme principal -----##
affichage(cases) # Affichage dans la console
while somme == 0 and n <= 9:
[ligne, colonne] = demande(joueur) # demande() renvoie 2 valeurs
while cases[ligne][colonne] != 0: # Recherche d'une case vide
print('Case occupée')
[ligne, colonne] = demande(joueur)
cases[ligne][colonne] = joueur # On place 1 ou -1 dans cases
affichage(cases)
somme = verif(cases) # Vérification de l'alignement
joueur = -joueur # Passage au joueur suivant
n += 1 # Passage au tour suivant
if somme == 1:
print('Bravo joueur 1 !')
elif somme == -1:
print('Bravo joueur 2 !')
else:
print('Match nul !')
Vous pouvez télécharger l'intégralité du programme correspondant
en cliquant ici.