Considérons un graphe quelconque (orienté ou non orienté).

On appelle chaîne toute succession d'arêtes dont l'extrémité de l'une (sauf la dernière) est l'origine de la suivante.

Le nombre d'arêtes qui composent une chaîne est appelé longueur de la chaîne.

On appelle chaîne fermée toute chaîne dont l'origine et l'extrémité coïncident.

On appelle cycle toute chaîne fermée dont les arêtes sont toutes distinctes.

Exemple

Chaînes et cycles

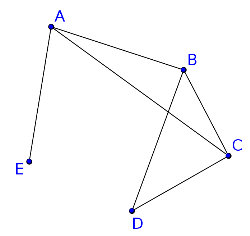	Dans le graphe ci-contre : E-A-C-B est un chaîne de longueur 3. E-A-C-B-A-E est une chaîne fermée de longueur 5. Ce n'est pas un cycle car l'arête A-E est parcourue deux fois. D-B-A-C-D est un cycle de longueur 4.

Soit A la matrice d'adjacence d'un graphe d'ordre \( n \in \mathbb{N}^{\star} \) dont les sommets sont numérotés de 1 à \( n \).

Le terme \( a_{ij} \) de la matrice \( A^k (k \in \mathbb{N^*}) \) est égal au nombre de chaînes de longueur \( k \) reliant les sommets \( i \) et \( j \) dans ce graphe.

Exemple

Combien existe t-il de chaînes de longueur 3 reliant le sommet B au sommet C ?

En numérotant les sommets de ce graphe par ordre alphabétique, sa matrice d'adjacence s'écrit \( A = \begin{pmatrix} 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \end{pmatrix} \) On a \( A^3 = \begin{pmatrix} 2 & 6 & 6 & 2 & 3 \\ 6 & 4 & 5 & 5 & 1 \\ 6 & 5 & 4 & 5 & 1 \\ 2 & 5 & 5 & 2 & 2 \\ 3 & 1 & 1 & 2 & 0 \end{pmatrix} \) Il existe donc 5 chaînes de longueur 3 reliant le sommet B au sommet C puisque \( a_{23} = a_{32} = 5 \).

Notion de connexité

Un graphe est dit connexe si deux de ses sommets quelconques sont toujours reliés par une chaîne.

Connexe ou pas connexe ?

	Le graphe ci-contre est connexe.
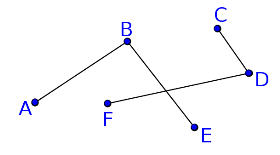	Le graphe ci-contre n'est pas connexe. Il est sécable en deux sous-graphes indépendants.

Un graphe est complet lorsque chacun de ses sommets est relié à tous les autres. Un graphe complet est donc nécessairement connexe mais la réciproque est fausse comme le montre l'exemple ci-dessus.

Chaînes et cycles eulériens

On appelle chaîne eulérienne d'un graphe toute chaîne qui contient une fois et une seule toutes les arêtes du graphe.

On appelle cycle eulérien une chaîne eulérienne fermée.

Existe t-il une chaîne ou un cycle eulérien dans chacun de ces graphes ?

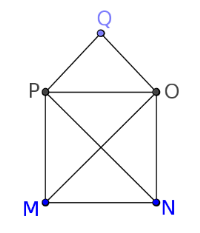	La chaîne M-P-Q-O-M-N-P-O-N est une chaîne eulérienne. En effet, cette chaîne contient bien 8 arêtes toutes distinctes.
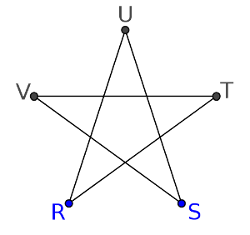	Le cycle R-U-S-V-T-R est un cycle eulérien.

Théorème d'Euler

Soit G un graphe connexe.

G admet un cycle eulérien si et seulement si tous les sommets de G sont de degré pair.

G admet une chaîne eulérienne (non fermée) si et seulement si le nombre de sommets de degré impair dans G est 2.

Si tel est le cas, les extrémités de la chaîne eulérienne sont les deux sommets de degré impair.