L'objectif de ce probème est de programmer la recherche de la longueur des plus courts chemins entre les sommets d'un graphe pondéré et orienté, par une méthode de complexité non optimale appelée l'algorithme de Floyd-Warshall.
Le principe de l'algorithme est le suivant : on numérote les sommets du graphe de $1$ à $n$ et on note pour tout les nombres entiers $i$, $j$ et $k$ dans $[1; n]$ le nombres $M_{i,j}^k$ comme étant la longueur du plus court chemin de longueur $k$ entre $i$ et $j$.
Pour tout couple $(i,j)$, $M^1_{i,j}$ est donc la longueur de l'arrête allant de $i$ à $j$ (si elle existe, et $\infty$ sinon), et la relation $$M^{k+1}_{i,j} = \min_l\left\{M^k_{i,l}+M^1_{l,j}\right\}$$ permet de définir par récurrence les coefficients des chemins de longueur $k$, ceux des chemins de longueur inférieure étant déjà connus.
L'algorithme de Floyd-Warshall, étant donnée les coefficients $M^1_{i,j}$ définis par un graphe orienté d'ordre $n$, calcule itérativement tous les coefficients $M^k_{i,j}$, pour $k$ allant de $2$ à $n$, puis donne la longueur du plus court chemin allant de $i$ à $j$ comme étant $\min_k\left\{ M^k_{i,j}\right\}.$
C'est la similitude entre la formule de récurrence $M^{k+1}_{i,j} = \min_l\left\{M^k_{i,l}+M^1_{l,j}\right\}$ et le calcul du coefficient $(i,j)$ dans un produit de matrices qui motive notre approche du problème.
Proposer une classe Matrice dont le constructeur prend en argument 2 entiers (le nombre de ligne et le nombre de colonnes) et la valeur initial de ses coefficients.
Elle devra proposer les méthodes __getitem__ et __setitem__ définies de façon à ce que M[i,j] permette d'accéder à l'élément de la ligne i et de la colonne j de la matrice M (numérotées à partir de 1), les opérateurs + et * correspondant au produit et à la somme habituels des matrices.
La méthode __repr__ devra aussi fournir une représentation commode pour l'affichage dans la console.
class Matrice:
def __init__(self,lig,col,vinit=0):
self.lig=lig
self.col=col
self.elt = [[]]*lig
self.vinit = vinit
for k in range(lig):
self.elt[k] = [self.vinit]*col
def __repr__(self):
chaine_aff = ""
for ligne in self.elt:
chaine_aff += str(ligne) + "\n"
return chaine_aff[:-1]
def __getitem__(self,pos):
if pos[0] > self.lig or pos[1] > self.col or pos[0] < 0 or pos[1] < 0:
return self.vinit
else:
return self.elt[pos[0]-1][pos[1]-1]
def __setitem__(self,pos,val):
if pos[0] <= self.lig and pos[1] <= self.col and pos[0] > 0 and pos[1] > 0:
self.elt[pos[0]-1][pos[1]-1] = val
def __add__(self,b):
res = Matrice(self.lig,self.col,self.vinit)
for i in range(1,self.lig+1):
for j in range(1,self.col+1):
res[i,j] = self[i,j]+b[i,j]
return res
def __mul__(self,b):
res = Matrice(self.lig,b.col,self.vinit)
for i in range(1,self.lig+1):
for j in range(1,self.col+1):
for k in range(1,self.col+1):
res[i,j] = res[i,j] + self[i,k]*b[k,j]
return res
Nous allons maintenant définir une classe dist dont le constructeur prend en argument un float et définissant les opérations + et * telles que, si A = dist(a) et B = dist(b), alors A+B = dist(min(a,b)) et A*B = dist(a+b). On doit également pouvoir comparer deux objets de type dist avec l'opérateur <, de façon à pouvoir appliquer la fonction min de python à des objets de type dist.
class dist:
def __init__(self, val):
self.valeur = val
def __add__(self,b):
return dist(min(self.valeur, b.valeur))
def __mul__(self,b):
return dist(self.valeur+b.valeur)
def __lt__(self,b):
return self.valeur < b.valeur
def __repr__(self):
return str(self.valeur)
Les structures de données définies dans les exercices précédents peuvent être combinées : c'est un intérêt majeur de la définition d'opérateurs. Si les coefficients de deux objets de type Matrice sont de type dist, alors ce sont les opérations entre objets de type dist qui sont utilisées dans les produits ou sommes de ces matrices. Il ne reste qu'à les utiliser pour rechercher la longueur du plus court chemin répondant à cette question du problème de spécialité du baccalauréat ES 2018 présentée ci-dessous.
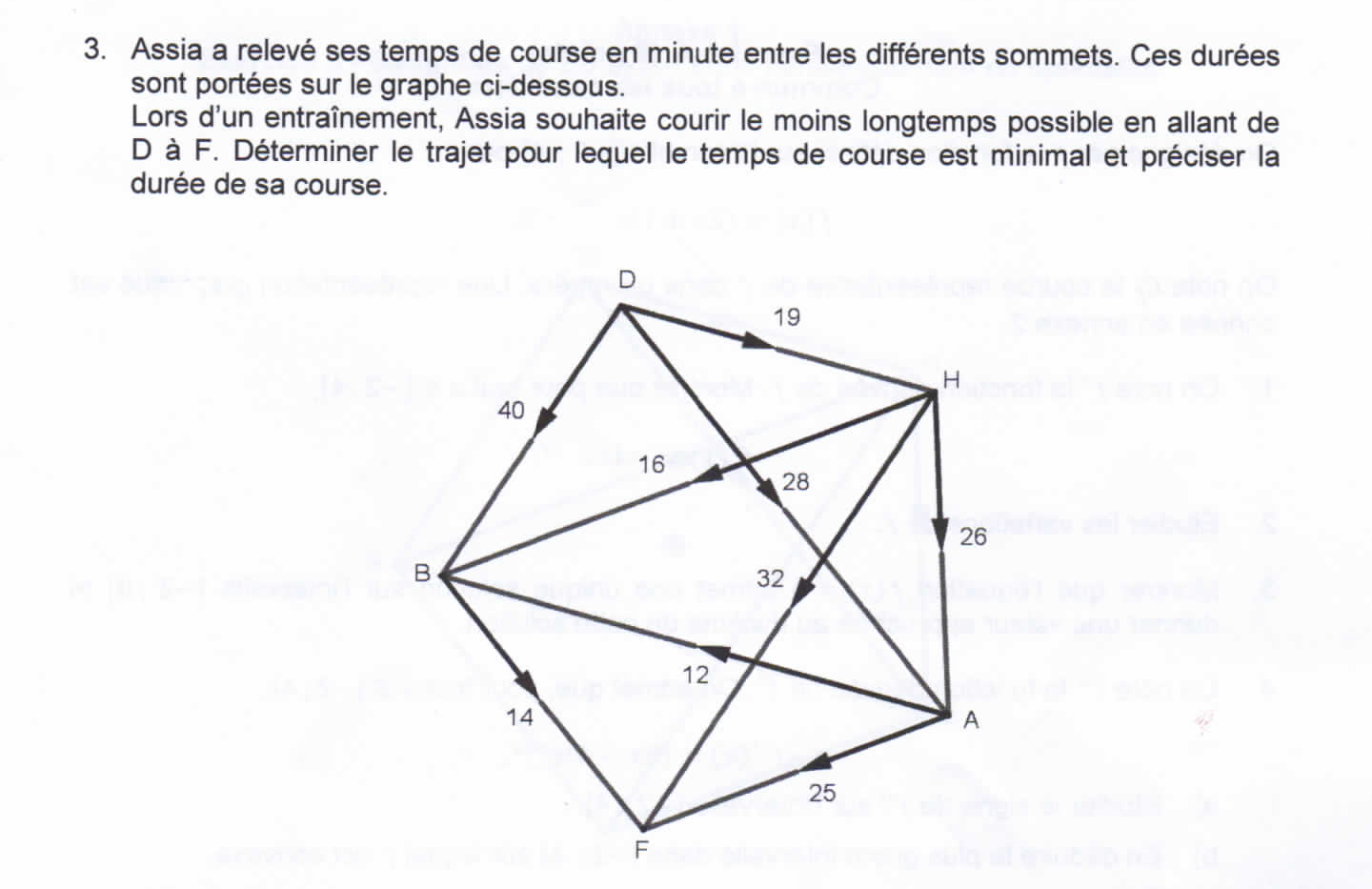
- mise en œuvre de l'algorithme
- les données du problème
- une réponse au problème
Étant donnée l'objet de type Matrice $u$ dont les coefficients de type dist reprennent les longueurs des arrêtes, alors $(u*u)[i,j]$ est la longueur du plus court chemin de longueur $2$ allant de $i$ à $j$. Plus généralement le produit (u*u*...*u) de $k$ copies de $u$ a pour coefficient [i,j] le nombre $M^k_{i,j}$. L'addition d'objets de type dist correspondant à l'opération $\min$, un objet $p$ de type matrice défini par $p = u + u*u + ... + u*u*...*u$ ($n$ fois) a donc pour coefficient [i,j] la longuer du plus court chemin de $i$ à $j$.
On reprend les données du graphe sous la forme d'un objet $u$ de type Matrice dont les coefficients sont des objets de dype dist reprenant les nombres $M^1_{i,j}$ de l'algorithme.
u=mat(5,5,dist(float('inf')))
u[1,2] = dist(12)
u[1,4] = dist(25)
u[2,4] = dist(14)
u[3,1] = dist(28)
u[3,2] = dist(40)
u[3,5] = dist(19)
u[5,1] = dist(26)
u[5,2] = dist(16)
u[5,4] = dist(32)
On applique l'agorithme en calculant $$p = u + u*u + u*u*u + u*u*u*u + u*u*u*u*u.$$ Le coefficient $p[3,4]$ donne le résultat.
u=Matrice(5,5,dist(float('inf')))
u[1,2] = dist(12)
u[1,4] = dist(25)
u[2,4] = dist(14)
u[3,1] = dist(28)
u[3,2] = dist(40)
u[3,5] = dist(19)
u[5,1] = dist(26)
u[5,2] = dist(16)
u[5,4] = dist(32)
p = u
for _ in range (4):
p = p*u + u
print ("La durée minimale d'un trajet de D à F est", p[3,4])
