Pour mieux saisir le poids de ce fichier, partons d'un fichier texte contenant comme unique ligne : 0 1 2 3 4 5 6 7 8 9.

Ouvrons ce fichier avec un lecteur hexadécimal :

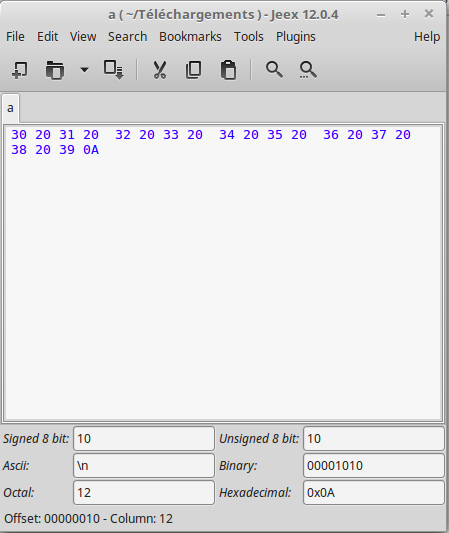
Les codes '20' qui s'affichent sont les codes ascii des espaces entre deux caractères. Le code '30' est le code ascii de '0'. Le code '0A' est le code de '\n' (saut de ligne).

Chacun de ces codes correspond à un octet.

L'ouverture du fichier Logo_Python.pgm avec un lecteur hexadécimal donne ceci pour le début de fichier :

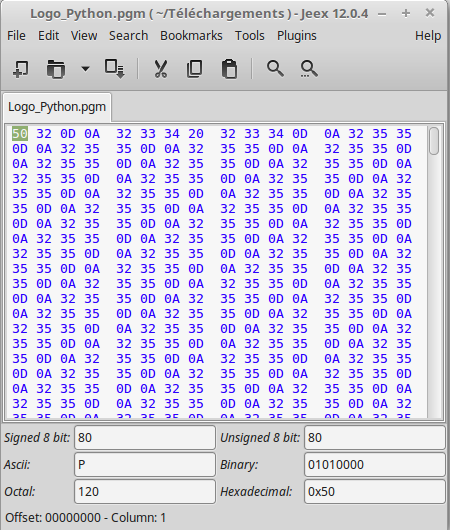
Le '50' qui apparaît au début est le code ascii de la lettre P du début du fichier.

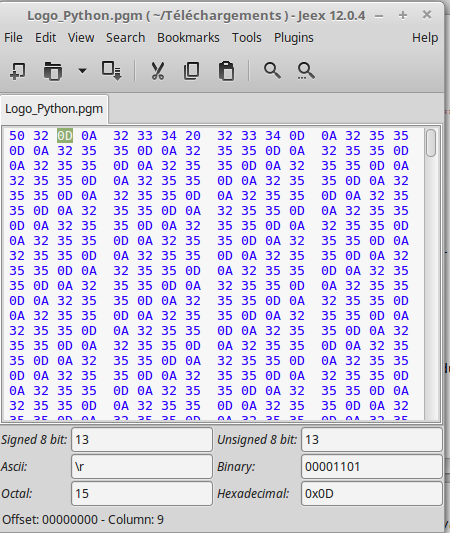
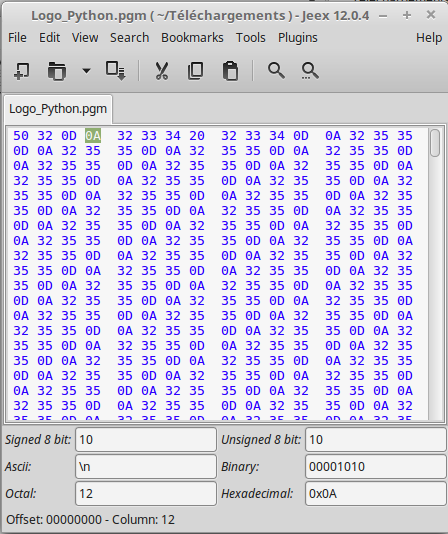
Les codes '0D' et '0A' correspondent aux deux caractères que l'on trouve à chaque fin de ligne d'un fichier (\r suivi de \n) encodé sous système d'exploitation Windows :

Le logo Python en nuances de gris comporte 234 × 234 = 54 756 pixels.
L'intensité maximale des niveaux de gris est 255.

Chaque intensité de gris nécessite de 1 à 3 caractères (0 : 1 caractère, 255 : 3 caractères), soit de 1 à 3 octets. Les 54 756 pixels nécessitent donc entre 54 756 octets et 54 756 × 3 octets.

On a constaté avec le lecteur hexadécimal que chaque passage à la ligne nécessitait ici deux octets (codage de '\r' suivi de '\n').

Comme la plupart des couleurs utilisées ici sont assez claires (parties blanches, parties gris clair), la plupart utilisent trois octets. On prévoit donc un fichier d'environ 234 × 234 × 5 = 273780 octets.

Lorsqu'on affiche les propriétés du fichier, on obtient 270 926 octets : certains pixels n'utilisent pas trois octets (code entre 0 et 99). On enlève donc un certain nombre d'octets, auxquels il faut finalement ajouter les octets nécessaires à l'entête.

Affinons.

• L'entête

  									P2
  									234 234
  									255
  								

  compte 11 caractères lettres et chiffres, 6 caractères pour les changements de ligne (trois fois '\r\n'), et 1 caractère espace dans la ligne deux, soit 18 caractères.
• Pour compter précisément le nombre d'octets pour coder les pixels, on va compter le nombre d'entiers entre 0 et 9, le nombre d'entiers entre 10 et 99 et le nombre d'entiers entre 100 et 255.
  Confions ce travail à un programme en Python :

  
  # travail sur le  fichier source
  with open('Logo_Python.pgm','r') as f :
  	# lecture du fichier et stockage dans une chaîne :
  	lecture = f.read() 
  	
  # transformation de la chaîne en liste :
  lecture = lecture.split()
   
  #on enlève les 4 premiers éléments correspondants à l'entête du fichier :
  lecture = lecture[4:]
  
  # on transforme chaque chaîne en un entier :
  lecture =  [ int(x) for x in lecture]
  
  # on compte les entiers entre 0 et 9 :
  compteUnChiffre = 0
  for x in lecture :
  	if 0 <= x <= 9 : compteUnChiffre += 1
  	
  # on compte les entiers entre 10 et 99 :
  compteDeuxChiffres = 0
  for x in lecture :
  	if 10 <= x <= 99 : compteDeuxChiffres += 1
  	
  # on compte les entiers entre 100 et 255 :
  compteTroisChiffres = 0
  for x in lecture :
  	if 100 <= x   : compteTroisChiffres += 1
  	
  	
  print(compteUnChiffre, compteDeuxChiffres, compteTroisChiffres)
  									

  La console affiche :

  0 2872 51884

• Bilan :
  • 18 octets pour l'entête.
  • 2872 × 2 octets pour coder les intensités de gris entre 10 et 99, auxquels on ajoute 2872 × 2 octets de changement de ligne.
  • 51884 × 3 octets pour coder les intensités de gris entre 100 et 255, auxquels on ajoute 51884 × 2 octets de changement de ligne.
  Le compte est bon : 270926 octets.

Ce fichier correspond à la même image au format Pgm. Mais on a gagné quelques octets. Où sont-ils gagnés ?

Le second fichier a été produit sous un système Linux. Le passage à la ligne s'y code par défaut avec le seul caractère nécessaire '\n', là où Windows utilise '\r\n'. On gagne donc un octet par ligne.

Ce fichier correspond à la même image au format Pgm. Mais on a gagné un nombre important d'octets. Où sont-ils gagnés ?

Ce troisième fichier utilise le format Pgm binaire au lieu du format Pgm ascii utilisé précédemment.

Dans ce format, tout entier entre 0 et 255 est codé sur un seul octet (0_dix = 00000000_deux, 255_dix = 11111111_deux). Le code gagne également sur les sauts de ligne (ouvrir le fichier avec un éditeur hexadécimal pour le constater).

Le premier carré comporte 50 × 50 = 2 500 pixels.
Au format Pbm, chaque pixel est codé par 0 ou 1, donc par un caractère (occupant un octet). Pour les pixels, on a donc déjà 2 500 octets.

Le code est réparti en 103 lignes. En l'ouvrant avec un éditeur hexadécimal, on constate que les passages à la ligne sont codés par un seul caractère '\n'. On a donc 2500 + 102 = 2602 octets.

Il reste l'entête :

								P1
								50 50
							

On a donc un total de 2609 octets pour cette image.

Le second carré comporte 50 × 50 = 2 500 pixels.
Au format Pgm, avec un niveau de gris maximal de 255, chaque pixel est codé sur un à trois octets. Le poids du fichier pour la partie pixels peut donc aller de 2500 à 7500 octets.

Entre le code de deux pixels est codé un espace ou un passage à la ligne (un caractère dans chaque cas pour ce fichier). On aura donc entre 2500+2500 = 5000 octets et 7500+2500 = 10 000 octets pour la partie pixels en ajoutant les séparations entre deux codes de pixels.

On constate d'ailleurs que le poids réel de ce fichier est 7588 octets.

Affinons les calculs

1. L'entête :

   									P2
   									50 50
   									255
   								

   occupe 9 octets lettres ou chiffres, un octet pour l'espace et trois octets '\n', soit 13 octets en tout.
2. On détermine maintenant avec le programme Python des solutions de l'exercice précédent le nombre d'intensités de gris de 1, 2 et 3 chiffres. On obtient : 625 entiers à un chiffre, 1250 entiers à deux chiffres et 625 entiers à trois chiffres. Soit un total de 625 × 1 + 1250 × 2 + 625 × 3 = 5000 octets.
3. À ces 5000 + 13 = 5013 octets, on ajoute le poids des espaces et '\n' : 5013 + 2500 = 7513 octets.
4. Il manque 75 octets. En regardant de plus près, on s'aperçoit que les passages à la ligne sont parfois précédés d'un blanc. Le décompte exact des blancs et des passages à la ligne peut être obtenu par le programme Python suivant :

   
   with open('Carre.pgm','r') as f :
   	# lecture du fichier et stockage dans une chaîne :
   	lecture = f.read()
    
   lecture = list(lecture)
   	
   # on compte les blancs et les '\n' :
   compteSeparateur = 0
   for x in lecture :
   	if x == ' ' or x == '\n'   : compteSeparateur += 1
   
   print(compteSeparateur)
   									

   On obtient le résultat 2579.
5. Le compte est bon : 9 octets d'entête (sans les séparateurs) + 5000 octets pour les intensités de gris + 2579 octets de séparateur = 7588 octets.

Le poids du dernier carré est de 23 766 octets.

Le dernier carré comporte 50 × 50 = 2 500 pixels.
Il est encodé dans le format Ppm avec une intensité maximale de 255. Chaque pixel nécessite entre 3 et 9 octets pour coder les intensités de rouge, vert, bleu. A cela on doit ajouter un caractère de séparateur entre deux intensités.

En ouvrant ce fichier avec un éditeur hexadécimal, on voit que s'ajoute une "difficulté" : les passages à la ligne ont été codés à la Windows par '\r\n'.
On constate également qu'on passe à la ligne après chaque pixel.

On peut donc prévoir entre 2500 × 3 + 2500 × 4 = 17500 octets et 2500 × 9 + 2500 × 4 = 32500 octets pour la partie pixels (séparateurs compris).

Reste à affiner comme pour le fichier précédent...

Ce fichier est l'image du dernier carré au format Ppm binaire plutôt que le format Ppm texte (ascii) comme précédemment : chaque triplet de pixels demande alors exactement trois octets. D'où un poids de l'ordre de 2500 × 3 = 7500 octets seulement.