Plus tard ! Les programmes ci-dessous ne sont pas à réaliser le jour de la formation (sauf s'il vous reste du temps bien évidemment). Ils sont là pour vous donner d'autres idées d'exercices (ou vous entraîner si besoin).

Créer en Noir & Blanc

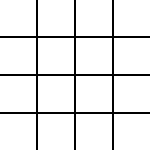
Concevoir les programmes en Python permettant d'obtenir les images suivantes, de dimensions 150*150.
Les lignes du quadrillage mesurent 2 pixels d'épaisseur...

Losange noir	Quadrillage sans bord	Un cercle de rayon 60px

Image n°1
Image n°2
Image n°3

Pour le losange noir, on reprend le script sur le losange évidé :


##----- Variables et constantes -----##
largeur = 150
hauteur = 150
demi = hauteur//2

##----- Ouverture/création des Fichiers -----##
f = open('Losange_Plein.pbm', 'w')

##------ En-tête ------##
f.write('P1 \n')								# P1 en ligne 1 pour déclarer le format .pbm puis passage à la ligne
f.write('{} {} \n'.format(largeur, hauteur))	# Largeur et hauteur de l'image, séparées par un espace

##------ Instructions principales ------##
for ligne in range(demi):						# Parcours de la 1ère moitié des lignes
	for colonne in range(largeur):
		if (colonne >= demi-1-ligne) and (colonne <= demi-1+ligne):
			f.write('1 \n')
		else :
			f.write('0 \n')
			
for ligne in range(demi):						# Parcours de la 2nde moitié des lignes
	for colonne in range(largeur):
		if (colonne >= ligne) and (colonne <= largeur-1-ligne):
			f.write('1 \n')
		else :
			f.write('0 \n')

##----- Fermeture des Fichiers -----##
f.close()

Pour le quadrillage sans bord, on ajoute 2 pixels à la largeur pour la bordure droite qui ne sera pas dessinée, on divise cette valeur par le nombre de colonnes puis on enlève les deux pixels correspondant à l'épaisseur de chaque ligne...


##----- Variables et constantes -----##
largeur, hauteur = 150, 150						# Largeur et hauteur de l'image, en pixels
colonnes, lignes = 4, 4                              
case_l = (largeur+2)//colonnes-2				# Largeur des cases                              
case_h = (hauteur+2)//lignes-2					# Hauteur des cases

##----- Ouverture/création des Fichiers -----##
f = open('Quadrillage.pbm', 'w')

##------ En-tête ------##
f.write('P1 \n')								# P1 en ligne 1 pour déclarer le format .pbm puis passage à la ligne
f.write('{} {} \n'.format(largeur, hauteur))	# Largeur et hauteur de l'image, séparées par un espace

##------ Instructions principales ------##
for l in range(lignes):
	for i in range(case_h):                         # Case du quadrillage par case
		for c in range(colonnes):
			for j in range(case_l):
				f.write('0 \n')
			if c!=colonnes-1:                       # Bord "droit" de la case
				f.write('1 1 \n')
	if l!=lignes-1:                                 # Ligne du bas de la case
		for c in range(2):
			for j in range(largeur):
				f.write('1 \n')

##----- Fermeture des Fichiers -----##
f.close()

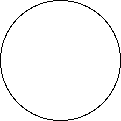
On rappelle que, dans un repère orthonormé, l'équation du cercle de centre \(I (x_I ; y_I)\) et de rayon \(r\) est \((x-x_I)^2+(y-y_I)^2 = r^2\).
La figure de droite (il y a bien une figure, zoomez pour voir...) permet de visualiser la différence entre pixel (plus petit élément d’une image) et point mathématique. Pour obtenir un « cercle épais », il faut une inégalité plus permissive que l'égalité.


##----- Variables et constantes -----##
largeur = 125
hauteur = 125
r = 60                          # rayon du cercle
abscisse = largeur//2           # abscisse du centre du cercle
ordonnee = hauteur//2         	# ordonnee du centre du cercle

##----- Ouverture/création des Fichiers -----##
f = open('Cercle02.pbm', 'w')

##------ En-tête ------##
f.write('P1 \n')								# P1 en ligne 1 pour déclarer le format .pbm puis passage à la ligne
f.write('{} {} \n'.format(largeur, hauteur))	# Largeur et hauteur de l'image, séparées par un espace

##------ Instructions principales ------##
a=int((r-0.5)**2)               # distance minimale entre un pixel et le centre
b=int((r+0.5)**2)               # distance maximale entre un pixel et le centre

for i in range(hauteur):        # Pour chaque numéro de ligne,
    for j in range(largeur):    # pour chaque numéro de colonne,

        if (j-abscisse)**2+(i-ordonnee)**2 in range(a,b+1): # Pixel entre 59 et 61 pixels du centre
            f.write('1 \n')     # pixel noir
        else :
            f.write('0 \n')     # pixel blanc

##----- Fermeture des Fichiers -----##
f.close()

Du Gris vers le Noir & Blanc

Cliquer sur l'image ci-contre pour télécharger le logo Python au format .pgm. L'image a été «préparée» : seul un pixel est encodé en intensité de gris (le maximum est 255) à chaque ligne.

Concevoir un programme permettant d'obtenir ce logo en noir et blanc. Pour cela, fixer un seuil d'intensité (ici élevée) en-deçà duquel le pixel sera affiché en noir, sinon il sera affiché en blanc.

Une piste
Une solution

Voici l'image finale à obtenir avec le seuil 208 :


##----- Ouverture des Fichiers -----##
fsource = open('Logo_Python.pgm', 'r')		# Ouverture (lecture) du fichier
fresult = open('Logo_Python_n_b.pgm', 'w')	# Ouverture (création) du fichier

##------ En-tête ------##
for i in range(3):                          # Les 3 lignes d'en-tête à recopier :
    fresult.write(fsource.readline())       # P2, dimensions, valeur max correspondant au blanc

##------ Instructions principales ------##
seuil = 208                                 # seuil d'intensité
for element in fsource:
	if int(element) < seuil:
		fresult.write('0 \n')
	else:
		fresult.write('255 \n')

##----- Fermeture des Fichiers -----##
fsource.close()
fresult.close()

Rectange dégradé

Les images au format .ppm doivent comporter sur les trois premières lignes :

P3 pour encoder le fichier au format .ppm ASCII ;
la largeur puis la hauteur de l'image, séparées par un espace ;
la valeur maximale utilisée pour estimer l'intensité maximale de chaque composante RVB (généralement, ce sera 255).

Concevoir un programme qui permet d'obtenir l'image d'un rectangle de 100 pixels de largeur et 256 pixels de hauteur, de couleur dégradée (linéaire) du noir (en haut) vers le rouge.

Essayer ensuite de produire d'autres dégradés plus originaux.

Une piste
Une autre piste
Une solution

Le saut à la ligne compte comme un espace (sous système Unix). Le plus intéressant est donc d'écrire :

sur la 4^ème ligne les trois composantes RVB (séparées par des espaces) du 1^er pixel ;
sur la 5^ème ligne les trois composantes RVB (séparées par des espaces) du 2^ème pixel ;
sur la 6^ème ligne les trois composantes RVB (séparées par des espaces) du 3^ème pixel ;
etc...

La 1^ère ligne comporte 100 pixels noirs de composante '0 0 0'.

La dernière ligne comporte 100 pixels rouges de composante '255 0 0'.


##----- Variables et constantes -----##
largeur, hauteur = 100, 256						# Largeur et hauteur de l'image, en pixels

##----- Ouverture/création des Fichiers -----##
f = open('Degrade_Rouge.ppm', 'w')

##------ En-tête ------##
f.write('P3 \n')								# Format .ppm
f.write('{} {} \n'.format(largeur, hauteur))	# Largeur et hauteur de l'image, séparées par un espace
f.write('255 \n')								# Maximum d'intensité des composantes

##------ Instructions principales ------##
for ligne in range(hauteur):
	for colonne in range(largeur):
		f.write('{} 0 0 \n'.format(ligne))		# Du noir '0 0 0' au rouge '255 0 0'
	f.write('\n')

##----- Fermeture des Fichiers -----##
f.close()

Seule la ligne 13 a été ajoutée, suivie des indentations nécessaires et d'un renommage du fichier à obtenir.


##----- Ouverture des fichiers -----##
fsource = open('materiel.txt', 'r')
fsortie = open('materiel_linux.txt', 'w')

##----- Variables et constantes -----##
liste_constructeurs = []
liste_quantite = []


##----- Programme principal -----##
for ligne in fsource:
    liste = ligne.split(" ")                    # Ligne transformée en liste de mots
    if 'linux' in liste:
        if liste[0] not in liste_constructeurs:
            liste_constructeurs.append(liste[0])
            liste_quantite.append(int(liste[2]))    # Quantité transformée en entier
        else:
            indice = liste_constructeurs.index(liste[0])
            liste_quantite[indice] += int(liste[2])

for i in range(len(liste_constructeurs)):
    fsortie.write(liste_constructeurs[i])
    fsortie.write(" ")
    fsortie.write(str(liste_quantite[i]))
    fsortie.write("\n")
    
##----- Fermeture des fichiers -----##
fsource.close()
fsortie.close()

Empilement de carrés

L'image ci-contre est constituée de sept carrés de couleur noir, rouge, vert, jaune, bleu, magenta et cyan.

Rappler les triplets RVB permettant de représenter les couleurs précédentes.
Concevoir une fonction carre(f, r, v, b) qui permet d'ajouter au fichier f un carré de 100 pixels de côtés et de couleur unie.
Utiliser cette fonction pour obtenir l'image ci-contre.

Un rappel
Une solution
Une autre solution

Couleur	Composante R	Composante V	Composante B
Noir	`0`	`0`	`0`
Rouge	`255`	`0`	`0`
Vert	`0`	`255`	`0`
Jaune	`255`	`255`	`0`
Bleu	`0`	`0`	`255`
Magenta	`255`	`0`	`255`
Cyan	`0`	`255`	`255`


##----- Définition des Fonctions -----##
def carre(f, r, v, b):
    """ Entrees : Un fichier f et trois entiers r, v et b compris entre 0 et 255
		Sorties : Ajoute au fichier f un carré de 100 pixels de côté et de couleur unie."""
    for i in range(100) :
        for j in range(100) :
            f.write('{0} {1} {2} \n'.format(r, v, b))

##----- Variables et constantes -----##
largeur, hauteur = 100, 700						# Largeur et hauteur de l'image, en pixels

##----- Ouverture/création des Fichiers -----##
f = open('Carres_Empiles.ppm', 'w')

##------ En-tête ------##
f.write('P3 \n')								# Format .ppm
f.write('{} {} \n'.format(largeur, hauteur))	# Largeur et hauteur de l'image, séparées par un espace
f.write('255 \n')								# Maximum d'intensité des composantes

##------ Instructions principales ------##
carre(f, 0, 0, 0)
carre(f, 255, 0, 0)
carre(f, 0, 255, 0)
carre(f, 255, 255, 0)
carre(f, 0, 0, 255)
carre(f, 255, 0, 255)
carre(f, 0, 255, 255)

##----- Fermeture des Fichiers -----##
f.close()

Cette variante mise sur une astuce et sur la lecture des nombres binaires. En effet,

l'entier 0 a pour écriture binaire '000' ;
l'entier 1 a pour écriture binaire '001' ;
l'entier 2 a pour écriture binaire '010' ;
l'entier 3 a pour écriture binaire '011' ;
l'entier 4 a pour écriture binaire '100' ;
l'entier 5 a pour écriture binaire '101' ;
l'entier 6 a pour écriture binaire '110' ;

Dans les écritures binaires ci-dessus, les '1' sont positionnés de manière «symétrique» avec les 255 des codes RVB des couleurs utilisées pour cette image. On définit donc une fonction binaire() qui renvoie sous forme de liste l'écriture binaire d'un entier.


##----- Définition des Fonctions -----##
def carre(f, r, v, b):
    """ Entrees : Un fichier f et trois entiers r, v et b compris entre 0 et 255
		Sorties : Ajoute au fichier f un carré de 100 pixels de côté et de couleur unie."""
    for i in range(100) :
        for j in range(100) :
            f.write('{0} {1} {2} \n'.format(r, v, b))

def binaire(n):
    """ Entrees : Un entier n
		Sorties : renvoie les chiffres de l'écriture binaire "inversée" de n sous
			la forme d'une liste (le chiffre de poids k est en indice k)"""
    l = []
    while n!=0:
        l.append(n%2)
        n = n//2
    while len(l)<3:                         # Pour avoir au minimum un triplet
        l.append(0)
    return l

##----- Variables et constantes -----##
largeur, hauteur = 100, 700						# Largeur et hauteur de l'image, en pixels

##----- Ouverture/création des Fichiers -----##
f = open('Carres_Empiles.ppm', 'w')

##------ En-tête ------##
f.write('P3 \n')								# Format .ppm
f.write('{} {} \n'.format(largeur, hauteur))	# Largeur et hauteur de l'image, séparées par un espace
f.write('255 \n')								# Maximum d'intensité des composantes

##------ Instructions principales ------##
for i in range(7) :                     		# Petite astuce : écriture binaire des nombres de 0 à 6...
    triplet = binaire(i)
    carre(f, 255*triplet[0], 255*triplet[1], 255*triplet[2])

##----- Fermeture des Fichiers -----##
f.close()

Concevoir pour les élèves

Reprendre l'image originale du logo Python, la convertir en .ppm en sélectionnant Ascii encoding à l'aide du logiciel IrfanView (ou autre) et concevoir un programme permettant de proposer aux élèves une image ayant un seul pixel encodé (c'est-à-dire un triplet) par ligne.

Une solution


##----- Ouverture des Fichiers -----##
fsource = open('Logo_Python_Original.ppm', 'r')		# Ouverture (lecture) du fichier
fresult = open('Logo_Python_Modifie.ppm', 'w')		# Ouverture (création) du fichier

##------ En-tête ------##
for i in range(3):                          # Les 3 lignes d'en-tête à recopier :
    fresult.write(fsource.readline())       # P2, dimensions, valeur max correspondant au blanc

##------ Instructions principales ------##
for element in fsource:						# Chaque ligne est une chaîne de caractères...
	valeurs = element.split()               # ...transformée en liste de nombres au format "str"
	for i in range(0, len(valeurs), 3):
		fresult.write('{0} {1} {2} \n'.format(valeurs[i], valeurs[i+1], valeurs[i+2]))

##----- Fermeture des Fichiers -----##
fsource.close()
fresult.close()

Palette complète de couleurs

Écrire un script permettant d'afficher la palette complète de couleur (comme ci-dessous, sans les textes) dans un carré de 511 pixels de côté.
Attention, le fichier texte est écrit de gauche à droite, de haut en bas...

Une solution


##----- Variables et constantes -----##
largeur, hauteur = 511, 511						# Largeur et hauteur de l'image, en pixels

##----- Ouverture/création des Fichiers -----##
f = open('palette.ppm', 'w')

##------ En-tête ------##
f.write('P3 \n')								# Format .ppm
f.write('{} {} \n'.format(largeur, hauteur))	# Largeur et hauteur de l'image, séparées par un espace
f.write('255 \n')								# Maximum d'intensité des composantes

##------ Instructions principales ------##
# On commence par le rectangle de hauteur 256 pixels et de largeur 511
for i in range(256):                # Pour chaque ligne
	v = 255-i                       # Composante verte dépend du numéro de ligne
	for j in range(511):            # Pour chaque colonne
		if j < 256:
			r = 255-j               # Composante rouge diminue sur le 1er "carré"
			b = 0                   # Composante bleue nulle
		else:
			b = j-255               # Composante bleue augmente sur le 2nd "carré"
			r = 0                   # Composante rouge nulle
		f.write('{0} {1} {2} \n'.format(r, v, b))

# Puis un carré blanc qui précède un rectangle de dimensions 255*256
for i in range(256):                # Pour chaque ligne
	for j in range(511):            # Pour chaque colonne
		if j < 255:                 # Carré blanc
			r = v = b = 255
		else:
			r = i                   # Composante rouge dépend du numéro de ligne
			v = 0                   # Composante verte nulle
			b = j-255               # Composante bleue augmente sur le 2nd "carré"
		f.write('{0} {1} {2} \n'.format(r, v, b))

##----- Fermeture des Fichiers -----##
f.close()

Un dégradé linéaire

Cet exercice a pour but de concevoir le dégradé ci-dessous de 100 pixels de hauteur et composé de 1280 couleurs, du rouge au violet (en fait, il n'y aura que 1276 couleurs différentes si on chipote) :

Pour cela, on étudie une représentation graphique possible des composantes R, G, B dans un repère du plan pour un tel dégradé où deux composantes restent constantes tandis que la 3^ème varie de 0 à 255 ou de 255 à 0.

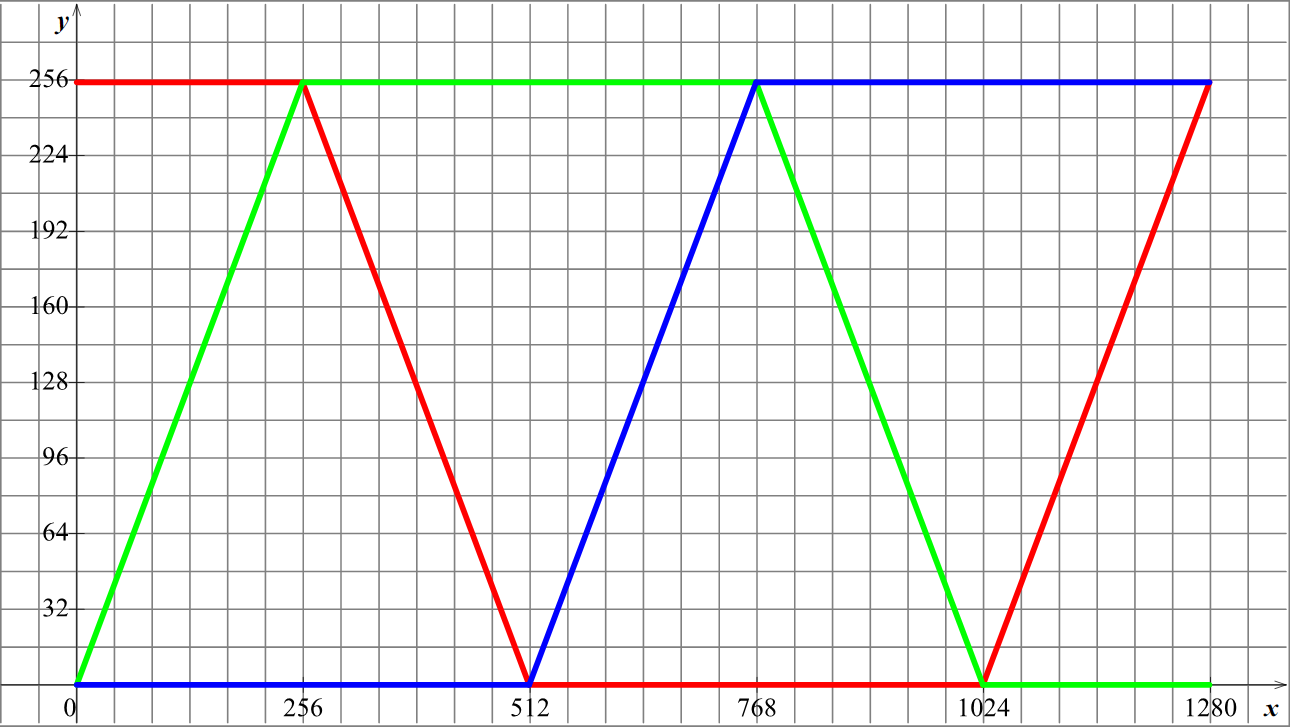
Programmer l'algorithme permettant d'obtenir cette image au format .ppm.

Une piste
Une autre piste
Une dernière piste
Une solution

Soit x la colonne du pixel à tracer. Déterminer les valeurs des composantes R, G, B de ce pixel en fonction de x.

La piste précédente conduit au tableau ci-dessous, à compléter...

Intervalle	Composante R	Composante G	Composante B
\(0 ⩽ x ⩽ 255 \)	\( 255 \)	\( x \)	\(0\)
\(256 ⩽ x ⩽ ... \)	.....	.....	.....
\(... ⩽ x ⩽ ... \)	.....	.....	.....
\(... ⩽ x ⩽ ... \)	.....	.....	.....
\(... ⩽ x ⩽ ... \)	.....	.....	.....

Le même tableau, complété cette fois-ci.

Intervalle	Composante R	Composante G	Composante B
\(0 ⩽ x ⩽ 255 \)	\( 255 \)	\( x \)	\(0\)
\(256 ⩽ x ⩽ 511 \)	\( 511-x \)	\( 255 \)	\( 0 \)
\(512 ⩽ x ⩽ 767 \)	\( 0 \)	\( 255 \)	\( x-512 \)
\(768 ⩽ x ⩽ 1023 \)	\( 0 \)	\( 1023-x \)	\( 255 \)
\(1024 ⩽ x ⩽ 1279 \)	\( x-1024 \)	\( 0 \)	\( 255 \)


##----- Variables et constantes -----##
largeur, hauteur = 1280, 100					# Largeur et hauteur de l'image, en pixels

##----- Ouverture/création des Fichiers -----##
f = open('Arc_En_Ciel.ppm', 'w')

##------ En-tête ------##
f.write('P3 \n')								# Format .ppm
f.write('{} {} \n'.format(largeur, hauteur))	# Largeur et hauteur de l'image, séparées par un espace
f.write('255 \n')								# Maximum d'intensité des composantes

##------ Instructions principales ------##
for ligne in range(hauteur):
	for x in range(largeur):
		if (0 <= x) and (x <= 255):
			r, v, b = 255, x, 0
		elif (256 <= x) and (x <= 511):
			r, v, b = 511-x, 255, 0
		elif (512 <= x) and (x <= 767):
			r, v, b = 0, 255, x-512
		elif (768 <= x) and (x <= 1023):
			r, v, b = 0, 1023-x, 255
		else:
			r, v, b = x-1024, 0, 255
		
		f.write('{} {} {} \n'.format(r, v, b))
	f.write('\n')

##----- Fermeture des Fichiers -----##
f.close()