Dans cette partie, nous allons étudier/concevoir quelques algorithmes qui permettront de manipuler des images. Nous verrons ensuite comment mettre en application ces algorithmes à l'aide de programmes écrits en Python.

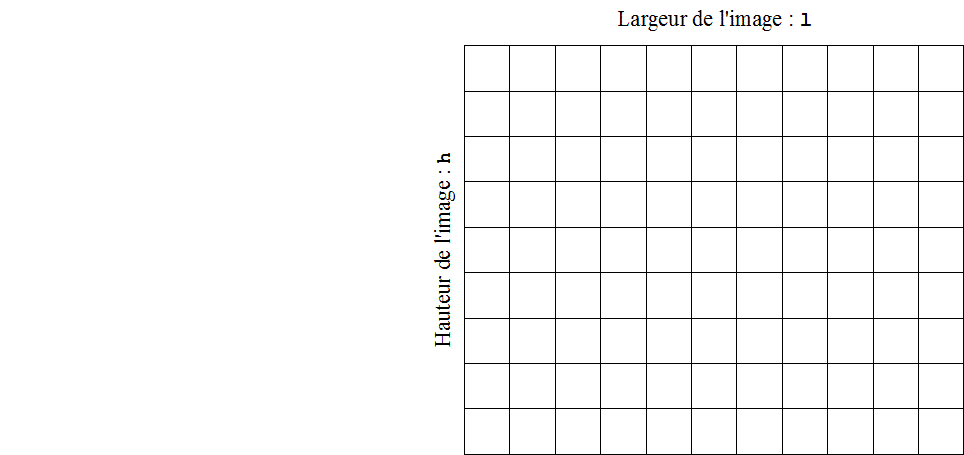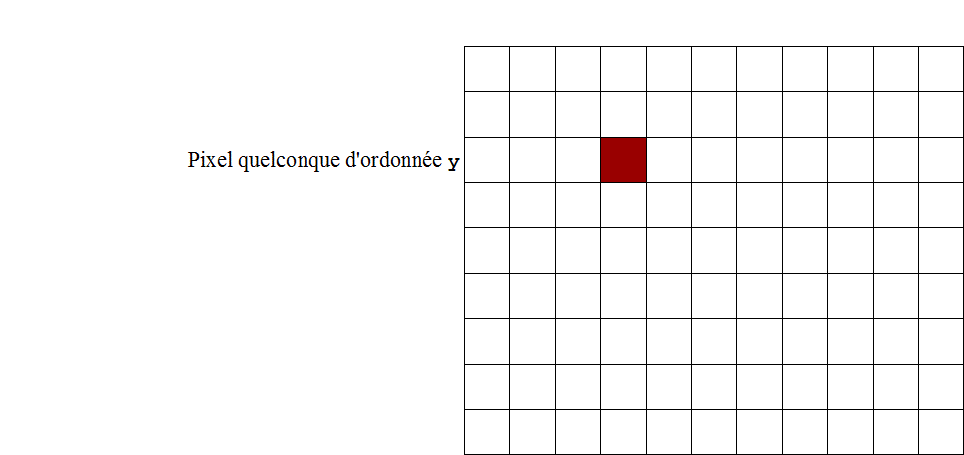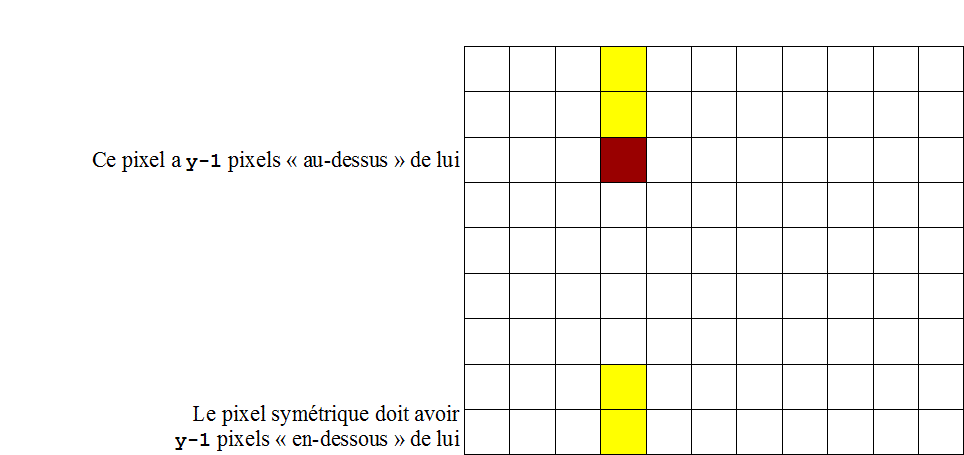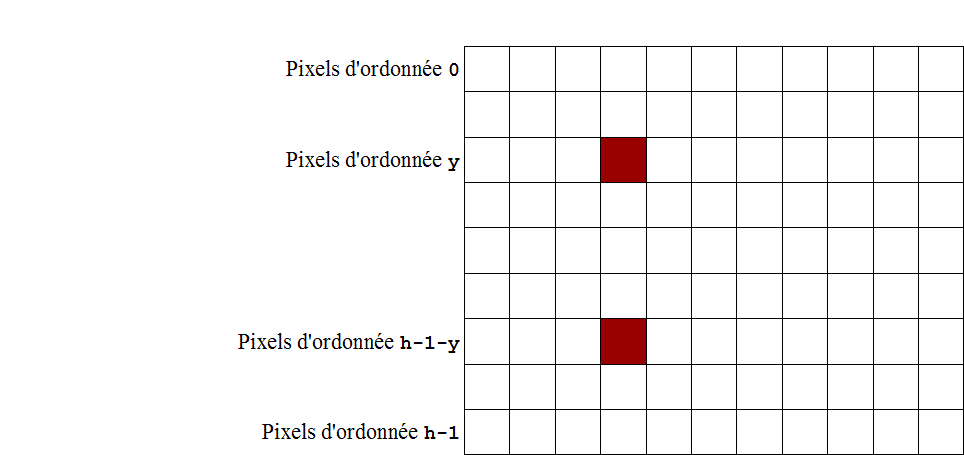
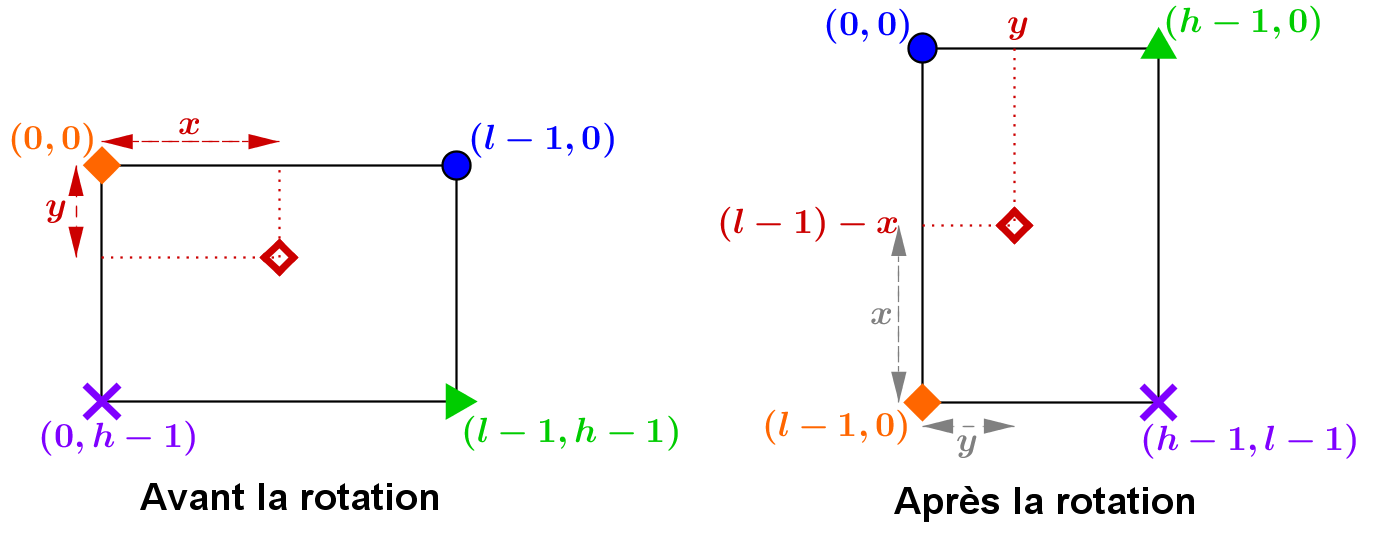
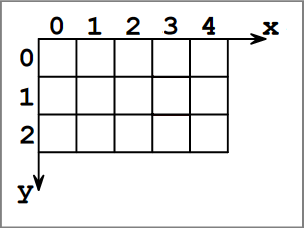
On considèrera dans chaque cas une image matricielle de hauteur h et de largeur l. Dans cette image, un pixel est repéré par ses coordonnées (x ; y) comme indiqué par l'image ci-contre.

1. Déterminer, en fonction de x et/ou de y, les coordonnées (x' ; y') du pixel correspondant dans la symétrie horizontale de cette image.
2. Même question avec une symétrie verticale de l'image.

Image originale	Symétrie horizontale	Symétrie verticale

• Illustration pour l'horizontale
• Réponse 1
• Réponse 2

Le pixel d'origine et le pixel correspondant ont la même abscisse (le pixel correspondant ne change pas de colonne). On en déduit les relations :

• x' = x
• y' = h-1-y

Le pixel d'origine et le pixel correspondant ont la même ordonnée (le pixel correspondant ne change pas de ligne). On en déduit les relations :

• x' = l-1-x
• y' = y

1. On considère une image en noir et blanc dans laquelle la composante «couleur» d'un pixel est notée nb, où nb prend pour valeur 0 ou 1.

   Image originale	Négatif de l'image

   Déterminer, en fonction de nb la composante couleur nb' du pixel correspondant dans le «négatif» de cette image.
2. On considère une image en nuances de gris dans laquelle la composante «couleur» d'un pixel est notée g, où g prend pour valeur un entier entre 0 et 255.

   Image originale	Négatif de l'image

   Déterminer, en fonction de g la composante couleur g' du pixel correspondant dans le «négatif» de cette image.
3. On considère une image en couleurs dans laquelle les composantes couleur d'un pixel sont notées (r, v, b) où r, v et b prennent pour valeur un entier entre 0 et 255.

   Image originale	Négatif de l'image

   Déterminer, en fonction de r, v et b les composantes couleurs (r', v', b') du pixel correspondant dans le «négatif» de cette image.

Déterminer, en fonction de x et/ou de y, les coordonnées (x' ; y') du pixel correspondant dans la rotation directe d'angle $\frac{\pi}{2}$ de cette image.

Image originale	Rotation d'angle $\frac{\pi}{2}$

• Une illustration
• Réponse

L'image n'est pas modifiée, elle est simplement tournée. Pour déterminer les opérations mathématiques à effectuer, le plus simple est de réaliser un schéma de l'image dans lequel on place un pixel de coordonnées (x ; y) avant la rotation, puis le même pixel après la rotation. En déterminant ses nouvelles coordonnées à partir du pixel haut-gauche de l'image tournée, on peut en déduire les calculs à effectuer sur les coordonnées (x ; y) d'origine.

Le pixel d'origine et le pixel correspondant n'ont ni la même abscisse, ni la même ordonnée. On déduit de l'illustration précédente les relations :

• x' = y
• y' = l-1-x

1. On considère une image en couleurs dans laquelle les composantes couleur d'un pixel sont notées (r, v, b) où r, v et b prennent pour valeur un entier entre 0 et 255.

   Image originale	Image en nuance de gris

   Déterminer, en fonction de r, v et b la composante g du pixel correspondant dans la représentation en nuances de gris de cette image.
2. On considère une image en nuances de gris dans laquelle la composante couleur d'un pixel est notée g où g prend pour valeur un entier entre 0 et 255.

   Image en nuances de gris	Image en noir et blanc

   Déterminer, en fonction de g la composante nb du pixel correspondant dans la représentation en noir et blanc de cette image.

Si g > 145 Alors nb ← 1
Sinon nb ← 0