Formation I.S.N.

Pour s'entraîner

Exercice 1

  1. Écrire une fonction max2 qui prend en arguments deux valeurs et renvoie la plus grande.
  2. Écrire une fonction repete qui répète le mot ’ISN’ un certain nombre de fois au choix.
  3. Écrire une fonction tirage qui tire au sort un nombre entier entre deux bornes données en arguments. On pourra utiliser les fonctions du paquet random.
  4. Écrire une fonction constructible qui décide s’il est possible de construire un triangle avec trois segments de mesures données.
  5. Écrire une fonction max3 qui prend en argument trois valeurs et renvoie la plus grande, en utilisant la fonction max2 de la première question.
  • Solution ?

Question 1


					def max2(a, b):   # fonction de deux arguments : a et b
						if a <= b:
							m = b     # une utilise une variable locale m
						else:
							m = a
						return m      # On peut utiliser deux return car seule une partie du
									  # test est interprétée : ce qui suit le if ou le else


Question 2


					def repete(n):
						m = 'ISN '
						return n*m


Question 3


					from random import *
					def tirage(a, b):
						return randint(a,b) # On utilise la fonction randint :
											# voir aide du paquet random en faisant help("random")


Question 4


					def constructible(a, b, c):
						if a < b + c and b < a + c and c < a + b:
							print("On peut construire le triangle")
						else:
							print("On ne peut pas construire le triangle")


Question 5


					def max3(a, b, c):
						return max2(max2(a,b),c)
					# on trouve le max de a et b avec max2 et le max entre le maximum précédent et la dernière valeur c.


Exercice 2

  1. Utiliser la fonction input pour écrire un programme qui demande en entrée la longueur de chaque côté d’un triangle (en cm) et renvoie son aire en sortie.
  2. (Source Wikipédia) La formule de Héron présente une instabilité lors du calcul numérique, qui se manifeste pour les triangles en épingle, c’est-à-dire dont un côté est de dimension très petite par rapport aux autres (confrontation de petites et grandes valeurs).

    En choisissant les noms de côtés de sorte à ce que a > b > c, et en réorganisant les termes de façon à optimiser les grandeurs ajoutées ou soustraites, on obtient la formule de Kahan, plus stable :

    \[ \frac{1}{4} \sqrt{(a+(b+c))(a+(b-c))(c-(a-b))(c+(a-b))} \]

    Montrer que la formule ci-dessus est correcte en vous appuyant sur la formule de Héron, éditer un nouveau programme utilisant cette formule de Kahan, puis tester les deux programmes avec des valeurs extrêmes (exemple : a = b = 1000000000 et c = 0,000000001).

  • Piste ?
  • Solution ?

Question 1 : Utiliser la formule de Héron. On testera le programme à l’aide d’un triangle rectangle (dimensions de votre choix) dont l’aire est facile à calculer.

Question 1


					from math import sqrt
					a=float(input("saisir a (en cm) : "))
					b=float(input("saisir b (en cm) : "))
					c=float(input("saisir c (en cm) : "))
					s=(a+b+c)/2
					Aire=sqrt(s*(s-a)*(s-b)*(s-c))
					print("L'aire du triangle est",Aire,"cm²")


Question 2


					from math import sqrt
					a=float(input("saisir le plus grand côté a (en cm) : "))
					b=float(input("saisir le côté moyen b (en cm) : "))
					c=float(input("saisir c le petit côté c (en cm) : "))
					s=(a+b+c)/2
					Aire=(1/4)*sqrt((a+(b+c))*(c-(a-b))*(c+(a-b))*(a+(b-c)))
					print("L'aire du triangle est",Aire,"cm²")

Exercice 3

Écrire une fonction table9 qui produit l’affichage suivant lorsqu’on l’appelle :console

  • Piste ?
  • Solution ?
Se souvenir de la boucle for et de l'argument à rajouter à la fonction print() pour empêcher le retour à la ligne. 

					def table9():
						for k in range(11):
							print(k*9,end=" ")

					table9()

Exercice 4

Écrire une fonction table9triple qui produit l’affichage suivant lorsqu’on l’appelle (utiliser la fonction de l’exercice précédent dans le corps de la fonction table9triple) :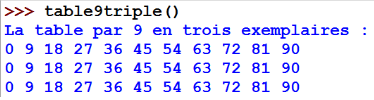console

  • Solution ?

					def table9():
						for k in range(11):
							print(k*9,end=' ')
						print()


					def table9triple():
						print('La table par 9 en trois exemplaires :')
						table9()
						table9()
						table9()

					table9triple()

ou bien, plus élégant...


					def table9():
						for k in range(11):
							print(k*9,end=' ')
						print()


					def table9triple():
						print('La table par 9 en trois exemplaires :')
						for k in range(3):
							table9()

					table9triple()

Exercice 5

Écrire une fonction qui prend en paramètres deux nombres x et y et renvoie le résultat de x²+ y². On utilisera l’instruction return.

Pour information, la représentation graphique de cette fonction de deux variables dans un repère orthonormé de l’espace (paraboloïde) :

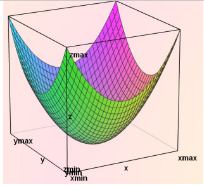
console

  • Solution ?

					a,b=2,3

					def f(x,y):
						return x**2+y**2

					print(f(a,b))

Exercice 6

  1. Écrire une fonction table avec un argument n qui produit l’affichage de la table de n a l’appel table(n).

    Tester l’instruction table(2) dans le Shell.

  2. Tester dans le Shell les instructions suivantes : console

    Qu’obtient-on ? Ainsi on peut remplacer le paramètre d’une fonction par une variable.

  3. Transformer la fonction de la première question en une fonction fragmentable de 3 paramètres telle que l’appel fragmentable(8,13,17) produise l’affichage :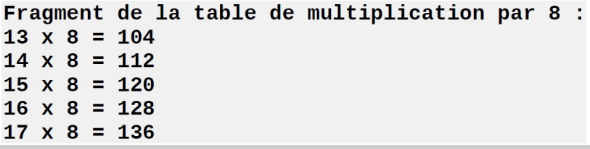 console
  • Solution ?

Question 1


					def table(n):
						for k in range(11):
							print(k*n,end=" ")


Question 2


					def table(n):
						for k in range(11):
							print(k * n, end=" ")

					a = 1
					while a < 20:
						table(a)
						# print() pour sauter une ligne entre les tables
						a = a + 1


Question 3


					def fragmentable(n, debut, fin):
						for k in range(debut, fin+1):
							print(k,"*",n,"=",k*n)

Exercice 7

Écrire un script qui demande à l'utilisateur le rayon d'une sphère et qui affiche son volume.

  • Solution ?

					def cube(n):
						return n**3
					def VolumeSphere(r):
						return 4 * 3.1416 * cube(r) / 3
					r = float(input("Entrer la valeur du rayon r : "))
					print("Le volume de cette sphère vaut : ", VolumeSphere(r))

Exercice 8

  1. Tester les deux scripts suivants : 
    
				from turtle import *
				forward(120)
				left(90)
				color("red")
				forward(80)

				reset()
				a = 0
				while a < 12:
					a = a + 1
					forward(150)
					left(150)

    Les principales fonctions mises à votre disposition dans le module turtle sont les suivantes : console

    • Écrire une fonction carre permettant de tracer un carré rouge de coté 100 à l’appel de carre(100,’red’).
    • Écrire un script utilisant la fonction carre et donnant le résultat : console
    • Reprendre les deux questions précédentes en remplaçant le carré par un triangle équilatéral de côté 100 pixels.
  • Piste ?
  • Solution ?

Question 2

Utiliser une boucle for. Attention à bien calculer le bon angle de rotation selon le sens.

Question 2


					from turtle import *

					# Fonction carre
					def carre(taille, couleur):
						"fonction qui dessine un carré de taille et de couleur déterminées"
						color(couleur)
						for k in range(4):
							forward(taille)
							right(90)
							

					# Fonction triangle
					def triangle(taille, couleur):
						"fonction qui dessine un triangle équilatéral de taille et de couleur déterminées"
						color(couleur)
						for k in range(3):
							forward(taille)
							left(120)

Exercice 9

Écrire un script avec Python permettant d'obtenir la figure suivante :

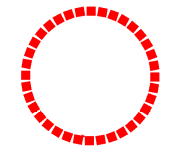
console
  • Piste ?
  • Solution ?
Définir une première fonction carre puis une deuxième fonction ncarre appelant n fois la fonction carre en faisant tourner le curseur du bon angle. 

					from turtle import *

					def carre(taille, couleur):
						"fonction qui dessine un carré de taille et de couleur déterminées"
						color(couleur)
						begin_fill()
						c = 0
						while c < 4:
							forward(taille) # en pixels
							right(90) # tourner le curseur à droite de 90 degrés
							c = c + 1
						end_fill()
							
					up() # relever le crayon
					goto(-150, -50) # reculer en haut à gauche

					def ncarre(n):
						"Choisir le nombre de carré(s) en argument"
						for i in range(n):
							down() # abaisser le crayon
							carre(25, 'red') # tracer un carré
							up() # relever le crayon
							forward(30) # avancer + loin
							left(10)

					ncarre(36) # appel de la fonction précédente pour dessiner 36 carrés pour faire une tour complet

Exercice 10

Écrire un script avec Python permettant d'obtenir la figure suivante :

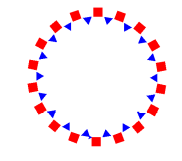
console

Pour en savoir plus sur le module Turtle, rentrer dans la partie suivante qui détaille les possibilités offertes par ce dernier.

  • Piste ?
  • Solution ?
Même idée de l'exercice précédent en introduisant une fonction triangle 

					from turtle import *

					def carre(taille, couleur):
						"fonction qui dessine un carré de taille et de couleur déterminées"
						color(couleur)
						begin_fill()
						c = 0
						while c < 4:
							forward(taille) # en pixels
							right(90) # tourner le curseur à droite de 90 degrés
							c = c + 1
						end_fill()

					# Fonction triangle
					def triangle(taille, couleur):
						"fonction qui dessine un triangle équilatéral de taille et de couleur déterminées"
						color(couleur)
						begin_fill()
						for k in range(3):
							forward(taille)
							left(120)
						end_fill()
							
					up() # relever le crayon
					goto(-150, -30) # reculer en haut à gauche

					def npolygone(n):
						"Choisir le nombre de carré(s) en argument"
						for i in range(n):
							down() # abaisser le crayon
							carre(25, 'red') # tracer un carré
							up() # relever le crayon
							forward(30) # avancer + loin
							left(10)
							triangle(25, 'blue')
							forward(30) # avancer + loin
							left(10)

					npolygone(18) # appel de la fonction précédente pour dessiner 18 séries carré+triangle