Formation I.S.N.

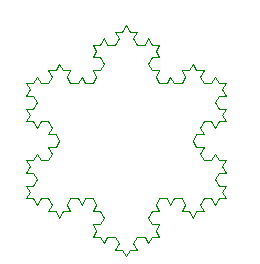
Récursivité floconneuse

la courbe de Von Koch

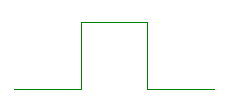
Proposer une tortue python récursive réalisant :

  • Avec n = 0 : koch 0
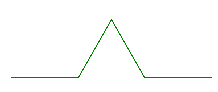
  • Avec n = 1 : koch 1
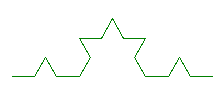
  • Avec n = 2 : koch 2
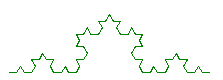
  • Avec n = 3 : koch 3
  • documentation
  • une aide
  • un code

On trouvera la doc sur le module turtle ici.

Le cas n = 1. 


import turtle as tl

def principeVonKoch(cote) :
	tl.forward(cote/3)
	tl.left(60)
	tl.forward(cote/3)
	tl.left(-120)
	tl.forward(cote/3)
	tl.left(60)
	tl.forward(cote/3)
		

tl.setheading(0) # orientation intiale de la tête : vers la droite de l'écran		
tl.hideturtle() # on cache la tortue
tl.speed(0)	 # on accélère la tortue
tl.color('green')
principeVonKoch( 200  ) 
tl.exitonclick() # pour  garder ouverte la fenêtre


import turtle as tl

 
		
def courbeVonKoch(  n, cote  ) :
	if n == 0 :
		tl.forward(cote)
	else :
		courbeVonKoch(n-1, cote/3)
		tl.left(60)
		courbeVonKoch(n-1, cote/3)
		tl.left(-120)
		courbeVonKoch(n-1, cote/3)
		tl.left(60)
		courbeVonKoch(n-1, cote/3)

tl.setheading(0) # orientation intiale de la tête : vers la droite de l'écran		
tl.hideturtle() # on cache la tortue
tl.speed(0)	 # on accélère la tortue
tl.color('green')
courbeVonKoch(  n = 3, cote = 200  ) 
tl.exitonclick() # pour  garder ouverte la fenêtre

le flocon

En déduire une fonction flocon

Avec n = 3 :
flocon

  • documentation
  • un code

On trouvera la doc sur le module turtle ici.


import turtle as tl

		
def courbeVonKoch(  n, cote  ) :
	if n == 0 :
		tl.forward(cote)
	else :
		courbeVonKoch(n-1, cote/3)
		tl.left(60)
		courbeVonKoch(n-1, cote/3)
		tl.left(-120)
		courbeVonKoch(n-1, cote/3)
		tl.left(60)
		courbeVonKoch(n-1, cote/3)
		
		
def flocon(n, cote) :
	for _ in range(3) :
		courbeVonKoch(  n, cote  )
		tl.left(-120)

tl.setheading(0) # orientation intiale de la tête : vers la droite de l'écran		
tl.hideturtle() # on cache la tortue
tl.speed(0)	 # on accélère la tortue
tl.color('green')
flocon(  n = 3, cote = 200  ) 
tl.exitonclick() # pour  garder ouverte la fenêtre

Variante sur la base

Modifier le principe de construction pour que le cas n = 1 devienne :
variante von koch
et tester un nouveau flocon.

  • documentation
  • un code

On trouvera la doc sur le module turtle ici.

Le principe générateur : 


import turtle as tl

		
def signalCarre( cote  ) :
	 
	tl.forward(cote/3)
	tl.left(90)
	tl.forward(cote/3)
	tl.right(90)
	tl.forward(cote/3)
	tl.right(90)
	tl.forward(cote/3)
	tl.left(90)
	tl.forward(cote/3)
		
	 
tl.setheading(0) # orientation intiale de la tête : vers la droite de l'écran		
tl.hideturtle() # on cache la tortue
tl.speed(0)	 # on accélère la tortue
tl.color('green')
signalCarre(  cote = 200  ) 
tl.exitonclick() # pour  garder ouverte la fenêtre

Avec : 


import turtle as tl

		
def courbeVonKoch(  n, cote  ) :
	if n == 0 :
		tl.forward(cote)
	else :
		courbeVonKoch(n-1, cote/3)
		tl.left(90)
		courbeVonKoch(n-1, cote/3)
		tl.right(90)
		courbeVonKoch(n-1, cote/3)
		tl.right(90)
		courbeVonKoch(n-1, cote/3)
		tl.left(90)
		courbeVonKoch(n-1, cote/3)
		
		
def flocon(n, cote) :
	for _ in range(3) :
		courbeVonKoch(  n, cote  )
		tl.left(-120)

tl.setheading(0) # orientation intiale de la tête : vers la droite de l'écran		
tl.hideturtle() # on cache la tortue
tl.speed(0)	 # on accélère la tortue
tl.color('green')
flocon(  n = 4, cote = 200  ) 
tl.exitonclick() # pour  garder ouverte la fenêtre

on obtient :
flocon écusson

Il peut être intéressant de jouer sur l'angle : 


import turtle as tl
from math import cos, pi


def cosinus(x) :
	""" x en degrés """
	return cos(x * 180/pi)
		
def Koch( profondeur,  angle, cote  ) :
	if profondeur == 0 :
		tl.forward(cote)
	else :
		cote =  cote/ (1 + cosinus(angle) )
		Koch(profondeur-1,  angle, cote )
		tl.left(angle)
		Koch(profondeur-1,  angle, cote )
		tl.right(2*angle)
		Koch(profondeur-1,   angle, cote )
		tl.left(angle)
		Koch(profondeur-1,   angle, cote )
		
		
def flocon(profondeur, direction, angle, cote) :
	for _ in range(3) :
		Koch(profondeur, direction, angle, cote )
		tl.left(-120)

tl.setheading(0) # orientation intiale de la tête : vers la droite de l'écran		
tl.hideturtle() # on cache la tortue
tl.speed(0)	 # on accélère la tortue
tl.color('green')
Koch( profondeur = 5,  angle = 85, cote = 200) 
tl.exitonclick() # pour  garder ouverte la fenêtre