BO : Représentation binaire
| Savoirs | Capacités | Observations |
|---|---|---|
| Représentation binaire : Un ordinateur est une machine qui manipule des valeurs numériques représentées sous forme binaire. |
Manipuler à l'aide d'opérations élémentaires les trois unités de base: bit, octet, mot. | On met en évidence, sous forme de questionnement, la présence du numérique dans la vie personnelle et professionnelle, au travers d'exemples. |
Pourquoi le codage binaire?
- Il faut au moins deux symboles.
- Choix indépendant de la nature des informations décrites.
- Plus simple à mettre en œuvre dans un ordinateur. Cela se réalise électriquement avec :
- Un interrupteur ouvert ou fermé.
- Un courant électrique présent ou absent.
- Un transistor polarisé ou pas.
- Un condensateur chargé ou pas….
- Capacité à résister au bruit :
- Avec le codage binaire, la taille en information du choix entre plusieurs options correspond au nombre de bits à utiliser.
Exemple :- 7 nombres entiers.
- 3 questions binaires maximum pour déterminer l’un d’eux.
- 3 bits pour les coder.
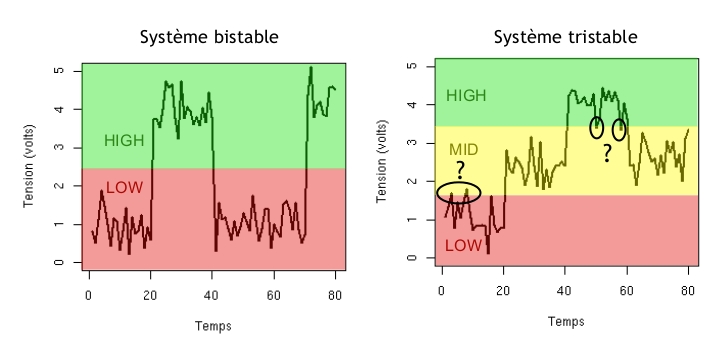
Pour un même niveau de bruit, se limiter à deux états permet de coder l’information de façon plus fiable