Système de numération

Système décimal

On utilise aujourd'hui universellement le système de numération décimale positionnelle.

Ainsi, 5123 peut s'écrire :
\( \begin{align} 5123 &= 5\times 1000 + 1\times100 + 2\times10 + 3\times1 \\ &= 5\times 10^3 + 1\times 10^2 + 2\times10^1 + 3\times10^0 \\ \end{align} \)

On dit que l'on utilise un système de base 10 (il y a 10 chiffres de 0 à 9).
L'avantage d'un tel système est que c'est la place d'un chiffre dans le nombre qui permet d'en connaître son poids (croissant d'un facteur 10 de 11 droite à gauche).

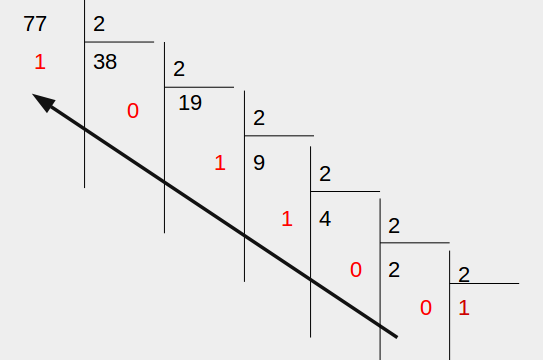
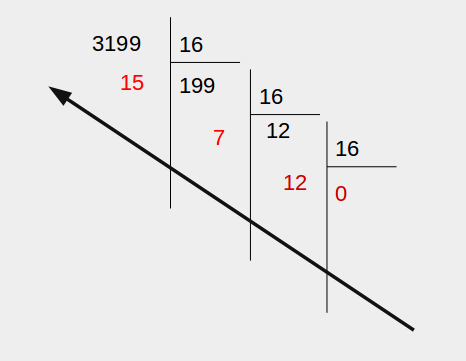
Système binaire

Il y a 10 sortes de personnes, celles qui comprennent la numération en binaire et les autres.

En informatique, outre la base 10, on utilise très fréquemment le système binaire (base 2) puisque l'algèbre booléenne est à la base de l'électronique numérique.

Deux symboles suffisent : 0 et 1.
Le principe reste le même, les puissances sont alors des puissances de 2.
Ainsi : \( 10111_2 = 1\times2^4 + 0\times2^3 + 1\times2^2 + 1\times2^1 + 1\times2^0\).

Et donc en base 10 ce nombre est : \( 10111_2 = 16 + 4 + 2 + 1 = 23_{10}\)

Conversion base 10 -> base 2

Pour obtenir une représentation utilisable dans des calculs, on passe de la numération à base 10 classique à la numération à base 2.

Première méthode

On soustrait les plus grandes puissances de deux successivement:

\( \begin{align} [45]_{10} &= 32 + 8 + 4 + 1\\ &= 2^5 + 2^3 + 2^2 + 2^0\\ &= 1\times2^5 + 0\times2^4 + 1\times 2^3 + 1\times2^2 + 0\times2^1 + 1\times2^0\\ \end{align} \)

Puis, \( [45]_{10} = [101101]_2 \)

Avec un tableau :

\( 2^5 \)	\( 2^4 \)	\( 2^3 \)	\( 2^2 \)	\( 2^1 \)	\( 2^0 \)
1	0	1	1	0	1

Deuxième méthode

On procède par division par 2 successives sur les quotients obtenus, jusqu'à obtenir un quotient nul:

Avec Python

L'écriture d'un entier binaire s'obtient avec la fonction bin. Elle est préfixée par '0b'


bin(13)

'0b1101'


0b1101  # par défaut Python représente toujours l’affichage en base 10


int('101110', 2)

def afficherBinaire(nombre):
    if nombre==0:
    	return ""
    else:
        return afficherBinaire(nombre // 2)+ str(nombre%2)

def affiche(n):
    for i in range (1,n+1):
        print (i,"----> ",afficherBinaire(i))

affiche(100)

Compléments

Nombre de bits

Pour coder des nombres entiers naturels compris entre 0 et 255, il suffit de 8 bits (un octet) car \(2^8 =256.\)
D'une manière générale un codage sur n bits pourra permettre de représenter les entiers naturels compris entre 0 et \(2^{n}-1.\)
Par exemple , avec 8 bits :
\([9]_{10} = [00000101]_2 \) \([128]_{10} = [10000000]_2 \)

Overflow

Dépassement de capacité
Exemple : A, B et C codés sur 1 octet A = 200
B = 100
C = A + B = 44
(le résultat se fait modulo 256)

La dernière retenue et le dernier 1 sont perdus.

L’arithmétique des ordinateurs n’est PAS celle (idéale) des mathématiques, car les ordinateurs travaillent avec un nombre fini de valeurs.

La base 16

On utilise aussi très souvent le système hexadécimal (base 16).

Simplicité d'utilisation et de représentation pour les mots machines.
Plus simple d'utilisation que le binaire.
Il faut six symboles supplémentaires :
- 10 \( \longrightarrow \) a
- 11 \( \longrightarrow \) b
- 12 \( \longrightarrow \) c
- 13 \( \longrightarrow \) d
- 14 \( \longrightarrow \) e
- 15 \( \longrightarrow \) f
Plus lisible pour un humain
- Adresse Mac : 48 bits (6 octets) : 5E:FF:56:A2:AF:15
- Adresse ipv6 :128 bits (16 octets) : 2001:0db8:0000:85a3:0000:0000:ac1f:8001

Exemples :
\([537]_{16} = 5\times16^2 + 3\times16 + 7\times1 = [1335]_{10}\)
\([d5f]_{16} = 13\times16^2 + 5\times16 + 15\times1 = [3423]_{10}\)

Pour la conversion en base 16 , d'un nombre en base 10, on peut aussi procèder par division par 16 successives sur les quotients obtenus, jusqu'à obtenir un quotient nul :

Pour convertir un nombre binaire en hexadécimal, il suffit de faire des groupes de quatre bits (en commençant depuis la droite).

\[ [\,\underbrace{1110}_{e}\,\underbrace{0111}_{7}\,]_2 = [e7]_{16} \]

Avec Python :


hex(49167)

'0xc00f'


print(0xc00f)

Avec les élèves

Exercices

Conversion base 10 → base 2.
Conversion base 2 → base 10.
Conversion base 16 → base 10.
Conversion base 10 → base 16.
Conversion base 16 → base 2.
Conversion base 2 → base 16.

Mini projet : convertisseurs
Période : Décembre.

Écrire un programme qui lit un entier positif ou nul, puis l'affiche en base binaire.
Écrire un programme qui lit un nombre positif ou nul en base binaire et qui affiche sa valeur en base 10.
Écrire un programme capable de convertir un nombre d'une base donnée en une autre.
Écrire un programme qui affiche une table de multiplication, mais dont tous les nombres sont affichés en base binaire.

Exercices

Enoncés
Solutions

1.
Trouver la représentation en base 10 du nombre \( [10110]_2 \).

2.
Trouver la représentation en base 2 du nombre \( [77]_{10} \).

3.
Trouver la représentation en base 10 du nombre \( [75b3]_{16} \).

4.
Trouver la représentation en base 16 du nombre \( [3199]_{10} \).

5.
Trouver la représentation en base 16 du nombre \( [1001101]_2 \).

6.
Quel est le plus grand entier non signé qu’on peut représenter en base 2 avec un mot de 8 bits ? un mot de 64 bits.

7.
Pour multiplier par dix un entier naturel exprimé en base dix, il suffit d’ajouter un 0 à sa droite, par exemple, 14 × 10 = 140.
Quelle est l’opération équivalente pour les entiers naturels exprimés en base deux ?
Exprimer en base deux les nombres 5, 10 et 20 pour vérifier cette remarque.

1.
\( [10110]_2 = 1\times2^4 + 0\times2^3 + 1\times2^2 + 1\times2^1 +0\times2^0 \)
\( \phantom{[10110]_2} = 1\times16 + 1\times4 + 1\times2 \)
\( \phantom{[10110]_2} = 22 \)

Conclusion \([10110]_2 = [22]_{10}\).

2.
On sait que \(2^0=1\), \(2^1=2\) \(2^2=4\), \(2^3=8\), \(2^4=16\), \(2^5=32\)et \(2^6=64\).
\([77]_{10} = 64 + 13\)
\( \phantom{[77]_{10}} = 64 + 8 + 5\)
\( \phantom{[77]_{10}} = 64 + 8 + 4 + 1\)
\( \phantom{[77]_{10}} = 2^6 + 2^3 + 2^2 + 2^0\)
\( \phantom{[77]_{10}} = [1001101]_2\)

Conclusion : \( [77]_{10} = [1001101]_2\).

3.
\([75b3]_{16} =7\times16^3 + 5\times16^2 + 11\times16^1 + 3\times16^0\)
\(\phantom{[75b3]_{16}} = 30131\)

Conclusion : \([75b3]_{16} = [30131]_{10}\)

4.
On sait que
\(2^0=1\), \(2^1=2\), \(2^2=4\), \(2^3=8\), \(2^4=16\), \(2^5=32\),
\(2^6=64\), \(2^7=128\), \(2^8=256\), \(2^9=512\), \(2^{10}=1024\) et \(2^{11}=2048\) (nous passons par l'écriture binaire en premier : voir l'exercice précédent).
\([3199]_{10} = 2048 + 1024 + 128 - 1 \)
\(\phantom{[3199]_{10}} = 2048 + 1024 + 64 + 32 + 16 + 8 + 4 + 2 + 1\)
\(\phantom{[3199]_{10}} = 2^{11} + 2^{10} + 2^6 + 2^5 + 2^4 + 2^3 + 2^2 + 2^1 + 2^0\)
\(\phantom{[3199]_{10}} = [\,\underbrace{1100}_{c}\,\underbrace{0111}_{7}\,\underbrace{1111}_{f}]_2\)
\(\phantom{[3199]_{10}} = [c7f]_{16}\)

Conclusion : \([3199]_{10} = [c7f]_{16}\)

5.
On fait des groupes de 4 bits en commençant par la droite.

Binaire	0100	1101
Pseudo-décimal	4	13
Hexadécimal	4	d

Conclusion \([1001101]_{2} = [4d]_{16}\)

6.
\( 2^8-1 = 255 \)
\(2^{64} -1 = 18446744073709551615 \)

7.
Pour multiplier par deux un entier naturel exprimé en base deux, il suffit d’ajouter un 0 à sa droite :
\([5]_{10} = [101]_{2}\)
\([10]_{10} = [1010]_{2}\)
\([20]_{10} = [10100]_{2}\)