SVG

Rotation

Définition

Le plan est supposé muni d'un repère orthonormé \( \left( O; \overrightarrow{i}, \overrightarrow{j} \right) \).

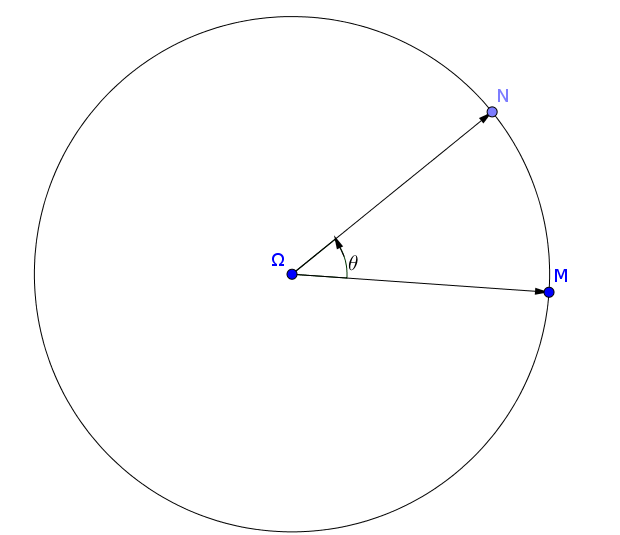
On appelle image du point M, par la rotation de centre \( \Omega \) et d'angle \( \theta \), le point N se trouvant sur le cercle de centre \( \Omega \) et de rayon \( \Omega M \) tel que l'angle orienté \( \left( \overrightarrow{\Omega M} ; \overrightarrow{\Omega N}\right) \) soit de mesure \( \theta \).

Définition de la rotation

La définition en termes de coordonnées : \[ \begin{cases} x_N = x_{\overrightarrow{\Omega M}} \cos(\theta) - y_{\overrightarrow{\Omega M}} \sin(\theta) + x_{\Omega} \\ y_N = x_{\overrightarrow{\Omega M}} \sin(\theta) + y_{\overrightarrow{\Omega M}} \cos(\theta) + y_{\Omega} \end{cases} \]

D'où vient cette formule sur les coordonnées ?

Plaçons nous dans le cadre des connaissances de première : on suppose que \( \Omega = O \) est le centre du repère et que le cercle est de rayon 1. Le cercle est donc le "cercle trigonométrique".

Dans cette situation, vous savez que les coordonnées de M sont de la forme \( \left( \cos(\alpha) ; \sin(\alpha) \right) \) où \( \alpha \) est l'angle \( \left( \overrightarrow{i} , \overrightarrow{OM} \right) \) entre le premier vecteur de la base et le vecteur \( \overrightarrow{OM} \). C'est en effet ainsi que l'on définit en seconde et en première cos et sin.

On obtient ensuite le point N "en tournant d'un angle \( \theta \) à partir de la position du point M". Les coordonnées du point N sont donc \( \left( \cos(\alpha + \theta) ; \sin(\alpha + \theta) \right) \).

On voit par ailleurs, en première S, les formules de trigonométrie suivante : \[ \forall a\in\mathbb{R}\ \ \forall b\in\mathbb{R} \ \ \ \cos(a+b)= \cos(a)\cos(b)-\sin(a)\sin(b) \text{ et } \sin(a+b) = \sin(a)\cos(b)+\sin(b)\cos(a) \]

Les coordonnées du point N sont donc : \[ \begin{cases} x_N = \cos(\alpha)\cos(\theta) - \sin(\alpha) \sin(\theta) \\ y_N = \sin(\alpha)\cos(\theta) + \sin(\theta) \cos(\alpha) \end{cases} \] c'est à dire : \[ \begin{cases} x_N = x_M\cos(\theta) - y_M \sin(\theta) \\ y_N = y_M \cos(\theta) + x_M\sin(\theta) \end{cases} \]

Il reste à tenir compte du rayon (homothétie) et du centre (translation) pour obtenir la formule dans le cas général énoncé plus haut.

Illustration avec du code SVG

On définit ci-dessous un triangle (avec l'instruction svg polygon). On définit ensuite l'image du triangle par la rotation de centre \( \Omega(70;70) \) et d'angle \( \frac{\pi}{4}\) radians.

<!DOCTYPE html>
<html lang="fr">
<head>
	<meta charset="utf-8">
	<title> xxx </title>
	<style>
	svg{
		border: 1px dotted black ;
	}
	</style>
</head>
<body>

<svg width="500" height="200" viewBox="0 -50 100 130">

<polygon points="10 10, 10 60, 30 50"
		 style="stroke:red; stroke-width:3;fill: none;" />

<g id="polyImage" style="stroke:green; stroke-width:3;fill: none;"></g>		 
 
 
<circle cx="70" cy="70" r="3" />
 
</svg>

<script>
var polyImage = document.getElementById("polyImage");
var c = Math.cos(Math.PI/4); //cosinus   de pi/4
var s = Math.sin(Math.PI/4); //  sinus de pi/4
var xcentre = 70, ycentre = 70; // coordonnées du centre de rotation
var abscisses = [10,10,30]; // abscisses des sommets du triangle de départ
var ordonnees = [10, 60, 50];// ordonnées des sommets du triangle de départ

var triangleImage = '<polygon points=" ';
// boucle de calculs des coordonnées des sommets images 
// à l'aide de la formule donnée plus haut :
for(let i = 0; i < abscisses.length; i++) {
	triangleImage += (c * (abscisses[i] - xcentre) - s * (ordonnees[i] - ycentre) + xcentre ) + ' ';
	triangleImage += (s * (abscisses[i] - xcentre) + c * (ordonnees[i] - ycentre) + ycentre) + ' ';
}
triangleImage += ' " /> ';
polyImage.innerHTML = triangleImage;
</script>

</body>
</html>

La rotation est faite dans le sens des aiguilles d'une montre contrairement à l'usage en mathématiques : cela est du au fait que l'axe des ordonnées est orienté vers le bas. Rappelons que le sens de rotation positif usuel en mathématiques n'est pas choisi par rapport au sens de rotation des aiguilles d'une montre : le quart de tour direct est celui qui envoie \( \overrightarrow{i} \), premier vecteur de la base, sur \( \overrightarrow{j} \), second vecteur de la base (ce qui correspond au sens des aiguilles d'une montre avec le choix d'un vecteur \( \overrightarrow{i} \) orienté de la gauche vers la droite et d'un vecteur \( \overrightarrow{j} \) orienté du haut vers le bas).

Rotation avec l'attribut `transform`.

On peut également utiliser les transformations prédéfinies en svg. L'angle est indiqué en degrés.
Pour une rotation de \( \frac{\pi}{4} \) radians, on indiquera donc un angle de \( 45^{\circ} \).

On utilisera donc : rotate( angle en degrés, abscisse du centre, ordonnée du centre).

La syntaxe allégée rotate(angle en degrés) prend le point origine comme centre de rotation.

Pour "tourner dans l'autre sens", on indiquera l'angle opposé :

Avec une balise `use`