Compter les opérations.

On écrit le programme de tri par sélection comme suit :



def indice_du_min(liste, depart):
	"""
	renvoie l'indice d'une valeur minimale
	parmi liste[depart], liste[depart+1], liste[depart+2], ..., liste[len(liste)-1]
	"""
	valeur_min = liste[depart]
	indice = depart
	for i in range(depart+1, len(liste)):
		if liste[i] < valeur_min :
			valeur_min, indice = liste[i], i
	return indice


def tri_selection(liste) :
	for i in range(len(liste)-1):
		m = indice_du_min(liste, i)
		liste[i], liste[m] = liste[m], liste[i]

Dans le programme précédent, comptez, en fonction de n = longueur de la liste donnée en entrée, le nombre de comparaisons qui a lieu entre deux éléments de la liste.
Vous compterez également le nombre d'échanges entre deux éléments de la liste et le nombre d'affectations.
Que peut-on dire du temps de calcul nécessaire à un tri de liste avec cet algorithme ?

Question 1
Question 2
Question 3

Les comparaisons entre éléments de la liste se font dans la fonction indice_du_min.


def indice_du_min(liste, depart):
	valeur_min = liste[depart]
	indice = depart
	for i in range(depart+1, len(liste)):
		if liste[i] < valeur_min :
			valeur_min, indice = liste[i], i
	return indice

Dans cette fonction, on compare les éléments liste[depart+1], liste[depart+2], ..., liste[len(liste)-1] à une valeur valeur_min.
Le nombre de comparaisons est, dans cette fonction, égal à len(liste)-1-depart = n-1-depart en notant n la longueur de la liste à trier.

Cette fonction est appelée dans la procédure tri_selection.


def tri_selection(liste) :
	for i in range(len(liste)-1):
		m = indice_du_min(liste, i)
		liste[i], liste[m] = liste[m], liste[i]

Elle est appelée avec les valeurs de depart = i : 0, 1, 2, ..., len(liste)-2.

Le nombre total de comparaisons est donc : \[ C_n = \sum_{i=0}^{n-2} (n-1-i) \] \[ C_n = (n-1)+(n-2)+(n-3)+ \dots + 1 \] On reconnaît là une progression arithmétique : \[ C_n = \frac{1}{2} n (n-1) \]

Nombre d'échanges

Les échanges entre deux éléments de la liste se font dans la procédure tri_selection.


def tri_selection(liste) :
	for i in range(len(liste)-1):
		m = indice_du_min(liste, i)
		liste[i], liste[m] = liste[m], liste[i]

Il y en a un pour chacune des valeurs de i de la boucle de cette procédure (i=0, 1, 2, ..., n-2). Il y a donc n-1 échanges.

Nombre d'affectations

Les affectations que l'on n'a pas déjà comptées dans les échanges ci-dessus se font dans la fonction indice_du_min.


def indice_du_min(liste, depart):
	valeur_min = liste[depart]
	indice = depart
	for i in range(depart+1, len(liste)):
		if liste[i] < valeur_min :
			valeur_min, indice = liste[i], i
	return indice

Il y en a au plus \( 2(n-i) \) (avec i = depart).
Comme cette fonction indice_du_min est appelée par la fonction tri_selection pour les valeurs i = 0, 1, 2, ..., n-2, le nombre de ces affectations est d'au plus : \[ A_n = \sum_{i = 0}^{n-2} 2\times(n-i) \] \[A_n = 2\times (n+(n-1)+(n-2)+\dots + 2) \] soit \[A_n = (n-1)(n+2)\]

On part de l'idée (à peu près correcte) que toute comparaison demandera toujours le même temps c, toute affectation le même temps a, tout échange d'éléments dans la liste le même temps e.

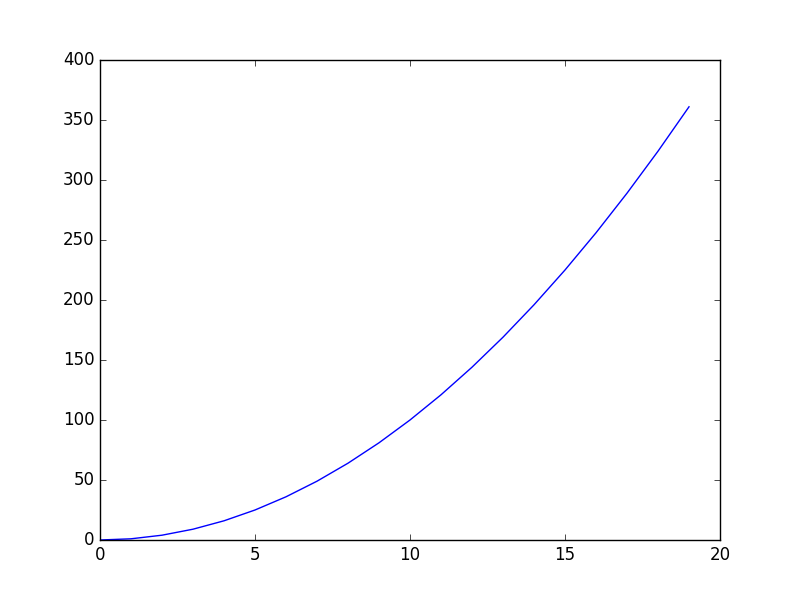
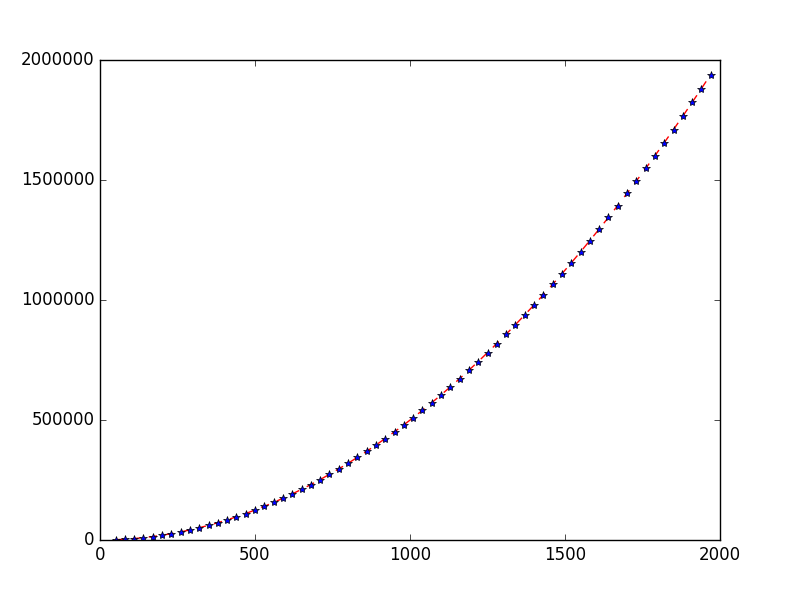
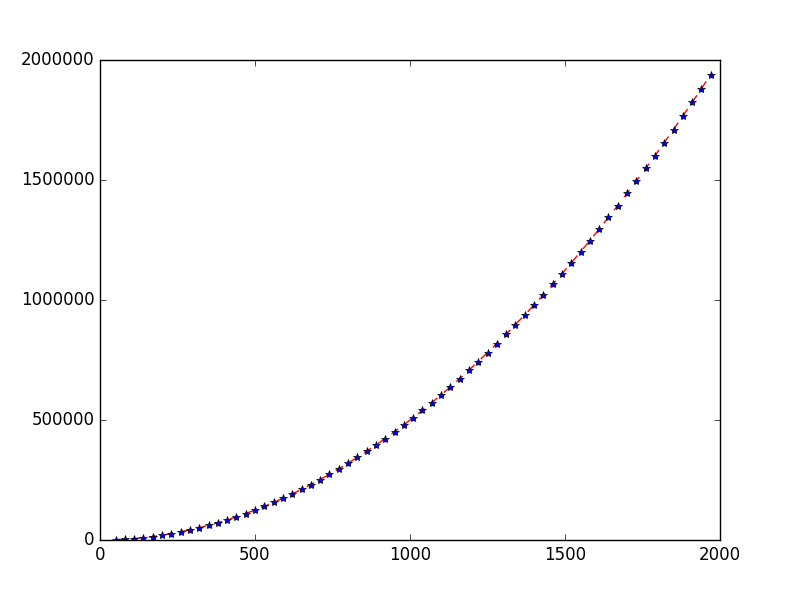
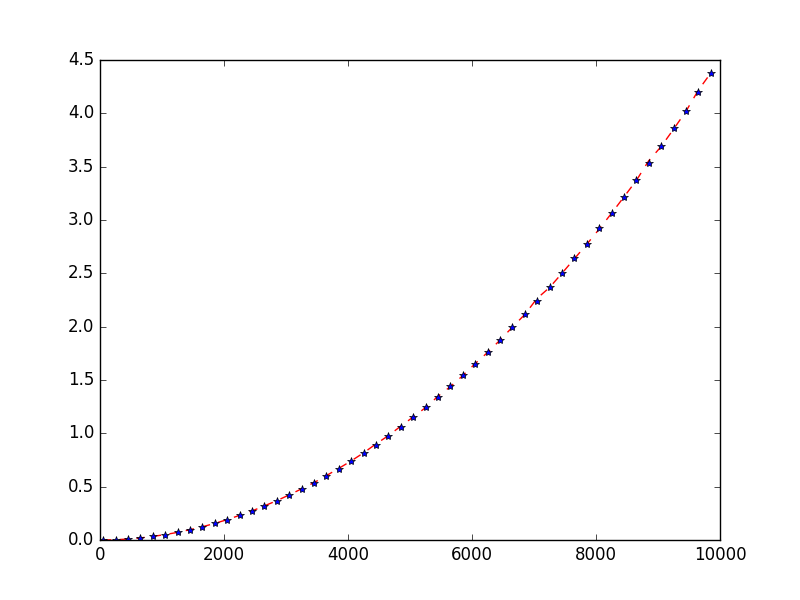
On a donc un temps d'exécution total majoré par : \[ T_n = c\times \frac{1}{2} n (n-1) + e \times (n-2) + a \times (n-1)(n+2) \] et (les comparaisons étant effectuées systématiquement) minoré par \[ T_n = c\times \frac{1}{2} n (n-1) \] Le temps d'exécution est donc compris entre deux polynômes de degré deux. C'est ce que l'on nomme une complexité temporelle quadratique.

Graphe de la fonction "nombre de comparaisons".

Dans l'exercice précédent, nous avons exprimé le nombre de comparaisons en fonction de la taille n de la liste donnée en entrée.

Nous allons "contrôler" notre décompte expérimentalement.

A l'aide d'un compteur dans le code, qui sera incrémenté à chaque nouvelle comparaison, ajouter au code du tri par sélection une fonction prenant en paramètre une longueur n de liste et retournant le nombre de comparaisons faites pour trier cette liste suivant le tri par sélection.
Obtenir une représentation graphique, à l'aide de python, de la fonction : taille de la liste ↦ nombre de comparaisons utilisées pour la trier.
Vérifier expérimentalement que la courbe obtenue correspond à la courbe de la fonction 'nombre de comparaisons' obtenue sous forme algébrique à l'exercice précédent.

Tracer une courbe
Q1
Q2

Voici une méthode simple pour une représentation graphique :


from pylab import plot, show

# liste des abscisses :
X = [ x for x in range(20) ]
# liste des ordonnées :
Y = [ x**2 for x in X]

# construction de la courbe et visualisation :
plot(X,Y)
show()

On obtient la courbe suivante :
fonction carré

Cette courbe est constituée des points de coordonnées (x,y) avec x dans la liste X et y = x**2 = élément de même rang, dans la liste Y, que x dans la liste X. Les points sont ensuite reliés. On peut éviter de relier les points et ne laisser réellement que les points définis par les listes X, Y de la façon suivante :


from pylab import plot, show

X = [ x for x in range(20) ]
Y = [ x**2 for x in X]

plot(X,Y,'.') # option points non reliés
show()


from random import randint # pour créer une liste au hasard

  

def tri_selection(liste) :
	
	nbComparaisons = 0
	
	def indice_du_min(liste, depart):
		nonlocal nbComparaisons
		
		valeur_min = liste[depart]
		indice = depart
		
		for i in range(depart+1, len(liste)):
			
			nbComparaisons += 1
			
			if liste[i] < valeur_min :
				valeur_min, indice = liste[i], i
		return indice
		
		
	for i in range(len(liste)-1):
		m = indice_du_min(liste, i)
		liste[i], liste[m] = liste[m], liste[i]
		
	return nbComparaisons



def compte_comparaisons(n) :
	"""
	n : longueur de liste testée.
	"""
	L = [randint(100,999) for i in range(n)]
	return tri_selection(L)


n = int(input("Entrez une longueur de liste : ")) 
print("Décompte du nombre de comparaisons par une variable compteur : ", compte_comparaisons(n) )
print("Valeur obtenue par la formule de l'exercice précédent : ", 1/2 * n * (n-1) )

On obtient par exemple :

Entrez une longueur de liste : 45
Décompte du nombre de comparaisons par une variable compteur :  990
Valeur obtenue par la formule de l'exercice précédent :  990.0

Code pour le tracé de courbe :


from pylab import plot, show
from random import randint # pour créer une liste au hasard




def tri_selection(liste) :
	
	nbComparaisons = 0
	
	def indice_du_min(liste, depart):
		nonlocal nbComparaisons
		
		valeur_min = liste[depart]
		indice = depart
		
		for i in range(depart+1, len(liste)):
			
			nbComparaisons += 1
			
			if liste[i] < valeur_min :
				valeur_min, indice = liste[i], i
		return indice
		
		
	for i in range(len(liste)-1):
		m = indice_du_min(liste, i)
		liste[i], liste[m] = liste[m], liste[i]
		
	return nbComparaisons



def compte_comparaisons(n) :
	"""
	n : longueur de liste testée.
	"""
	L = [randint(100,999) for i in range(n)]
	return tri_selection(L)
	
	
	

# une liste de tailles à tester (50, 50+30, 50+2*30, 50+3*30...) :
X = [ i for i in range(50, 2000, 30) ]
# liste des ordonnées :
Y = [ compte_comparaisons(n) for n in X]

plot(X,Y,'.')
show()

On obtient :

courbe de la fonction dénombrant les comparaisons.

On ajoute quelques lignes de code pour tracer sur le même graphique la courbe de la fonction \( n \longrightarrow \frac{1}{2} n(n-1) \) :


from pylab import plot, show
from random import randint # pour créer une liste au hasard




def tri_selection(liste) :
	
	nbComparaisons = 0
	
	def indice_du_min(liste, depart):
		nonlocal nbComparaisons
		
		valeur_min = liste[depart]
		indice = depart
		
		for i in range(depart+1, len(liste)):
			
			nbComparaisons += 1
			
			if liste[i] < valeur_min :
				valeur_min, indice = liste[i], i
		return indice
		
		
	for i in range(len(liste)-1):
		m = indice_du_min(liste, i)
		liste[i], liste[m] = liste[m], liste[i]
		
	return nbComparaisons



def compte_comparaisons(n) :
	"""
	n : longueur de liste testée.
	"""
	L = [randint(100,999) for i in range(n)]
	return tri_selection(L)
	
	
	

# une liste de tailles à tester (50, 50+30, 50+2*30, 50+3*30...) :
X = [ i for i in range(50, 2000, 30) ]
# liste des ordonnées :
Y = [ compte_comparaisons(n) for n in X]
YY = [ 1/2 * n * (n-1) for n in X]


# r-- : rouge pointillé pour la courbe 1
# b* : étoiles bleues pour la courbe 2
plot(X,Y,'r--', X, YY, 'b*')
show()

Les deux courbes se superposent évidemment :

Graphe et formule pour la fonction "nombre de comparaisons".

Dans l'exercice précédent, nous avons confirmé notre décompte expérimentalement. Nous voyons ici que les outils python auraient même permis d'obtenir la formule.

Pas de questions ici, déroulez les cartouches dans l'ordre. L'objectif est de préparer l'exercice suivant.

polyfit
utilisation

On utilise la fonction polyfit du module pylab.

Soit X une liste de nombres et Y une liste de nombres. polyfit(X,Y, 2) calculera un polynôme du second degré "au plus près de la courbe" définie par les points (x,y). (Nous ne détaillons pas ici plus avant en quel sens "au plus près" doit être compris.)

Avec l'instruction p=polyfit(X,Y,2), le polynôme de degré 2 "au plus près de la courbe" calculé par polyfit sera donné par : p[0]*x**2+p[1]*x+p[2].

On lance à nouveau notre fonction de comptage des comparaisons. Mais cette fois, la courbe n'est pas comparée à la formule déjà trouvée mais à la formule déterminée avec l'outil polyfit.


from pylab import plot, show, polyfit
from random import randint # pour créer une liste au hasard




def tri_selection(liste) :
	
	nbComparaisons = 0
	
	def indice_du_min(liste, depart):
		nonlocal nbComparaisons
		
		valeur_min = liste[depart]
		indice = depart
		
		for i in range(depart+1, len(liste)):
			
			nbComparaisons += 1
			
			if liste[i] < valeur_min :
				valeur_min, indice = liste[i], i
		return indice
		
		
	for i in range(len(liste)-1):
		m = indice_du_min(liste, i)
		liste[i], liste[m] = liste[m], liste[i]
		
	return nbComparaisons



def compte_comparaisons(n) :
	"""
	n : longueur de liste testée.
	"""
	L = [randint(100,999) for i in range(n)]
	return tri_selection(L)
	
	
	

# une liste de tailles à tester (50, 50+30, 50+2*30, 50+3*30...) :
X = [ i for i in range(50, 2000, 30) ]
# liste des ordonnées :
Y = [ compte_comparaisons(n) for n in X]
 
  
p = polyfit(X, Y, 2)
YY = [ p[0]*n**2 + p[1]*n + p[2] for n in X ] 


print(" p(x) = {}*x^2+{}*x+{}.".format(p[0], p[1],p[2] ) )


# r-- : rouge pointillé pour la courbe 1
# b* : étoiles bleues pour la courbe 2
plot(X,Y,'r--', X, YY, 'b*')
show()

On obtient :

p(x) = 0.5000000000000008*x^2+-0.5000000000007333*x+9.131883202823179e-11.

ce qui correspond bien à la formule déterminée par calcul lors du premier exercice.

On obtient le graphique suivant (sur lequel se superposent la courbe expérimentale des dénombrements de comparaisons et la courbe de degré 2 calculée par polyfit) :

Code pour le tracé de courbe :

On obtient :

On ajoute quelques lignes de code pour tracer sur le même graphique la courbe de la fonction \( n \longrightarrow \frac{1}{2} n(n-1) \) :


from pylab import plot, show
from random import randint # pour créer une liste au hasard




def tri_selection(liste) :
	
	nbComparaisons = 0
	
	def indice_du_min(liste, depart):
		nonlocal nbComparaisons
		
		valeur_min = liste[depart]
		indice = depart
		
		for i in range(depart+1, len(liste)):
			
			nbComparaisons += 1
			
			if liste[i] < valeur_min :
				valeur_min, indice = liste[i], i
		return indice
		
		
	for i in range(len(liste)-1):
		m = indice_du_min(liste, i)
		liste[i], liste[m] = liste[m], liste[i]
		
	return nbComparaisons



def compte_comparaisons(n) :
	"""
	n : longueur de liste testée.
	"""
	L = [randint(100,999) for i in range(n)]
	return tri_selection(L)
	
	
	

# une liste de tailles à tester (50, 50+30, 50+2*30, 50+3*30...) :
X = [ i for i in range(50, 2000, 30) ]
# liste des ordonnées :
Y = [ compte_comparaisons(n) for n in X]
YY = [ 1/2 * n * (n-1) for n in X]


# r-- : rouge pointillé pour la courbe 1
# b* : étoiles bleues pour la courbe 2
plot(X,Y,'r--', X, YY, 'b*')
show()

Les deux courbes se superposent évidemment :

Complexité du tri sélection

Utilisez time() pour évaluer le temps de calcul d'un tri sélection (en fonction de n = longueur de liste donnée en entrée). Puis utilisez l'outil polyfit pour "confirmer" expérimentalement que ce temps de calcul est approximativement une fonction du second degré de la variable n.

time
utilisation

La fonction time() du module time est documentée ainsi :

Return the time in seconds since the epoch as a floating point number. The specific date of the epoch and the handling of leap seconds is platform dependent. On Windows and most Unix systems, the epoch is January 1, 1970, 00:00:00 (UTC) and leap seconds are not counted towards the time in seconds since the epoch. This is commonly referred to as Unix time. To find out what the epoch is on a given platform, look at gmtime(0).

Note that even though the time is always returned as a floating point number, not all systems provide time with a better precision than 1 second. While this function normally returns non-decreasing values, it can return a lower value than a previous call if the system clock has been set back between the two calls.

The number returned by time() may be converted into a more common time format (i.e. year, month, day, hour, etc…) in UTC by passing it to gmtime() function or in local time by passing it to the localtime() function. In both cases a struct_time object is returned, from which the components of the calendar date may be accessed as attributes.


from pylab import plot, show, polyfit
from random import randint # pour créer une liste au hasard
from time import time



def tri_selection(liste) :
	
	def indice_du_min(liste, depart):
		valeur_min = liste[depart]
		indice = depart
		
		for i in range(depart+1, len(liste)):
			if liste[i] < valeur_min :
				valeur_min, indice = liste[i], i
		return indice
		
		
	tempsDebut = time()
		
	for i in range(len(liste)-1):
		m = indice_du_min(liste, i)
		liste[i], liste[m] = liste[m], liste[i]
		
	tempsFin  = time()
	
	# la fonction retourne le temps mis pour son exécution : 
	return tempsFin- tempsDebut


 

def temps_tri(n) :
	"""
	n : longueur de liste testée.
	"""
	L = [randint(100,999) for i in range(n)]
	return tri_selection(L)
		
	
	

# une liste de tailles à tester  :
X = [ i for i in range(50, 10000, 200) ]
# liste des ordonnées :
Y = [ temps_tri(n) for n in X]
 
  
p = polyfit(X, Y, 2)
YY = [ p[0]*n**2 + p[1]*n + p[2] for n in X ] 


print(" p(x) = {}*x^2+{}*x+{}.".format(p[0], p[1],p[2] ) )


# r-- : rouge pointillé pour la courbe 1
# b* : étoiles bleues pour la courbe 2
plot(X,Y,'r--', X, YY, 'b*')
show()

On obtient :

p(x) = 4.503773791449411e-08*x^2+3.773708518097925e-07*x+0.0009176820818899213.

On obtient le graphique suivant (sur lequel se trouvent la courbe expérimentale des temps de tri et la courbe de degré 2 approchée calculée par polyfit) :