Question de formules
Cette page en chantier permanent recense les formules mathématiques que j’aime bien pour diverses raisons. Certaines sont présentes dans Le Chuchoteur de formules de la Maison Poincaré, d’autres pas.
©Institut Henri Poincaré, Paris / Atelier Novembre, Du&Ma – Opixido
Formule de Heawood
Donne le nombre chromatique \(\chi\) d’une surface orientable de genre \(g\):
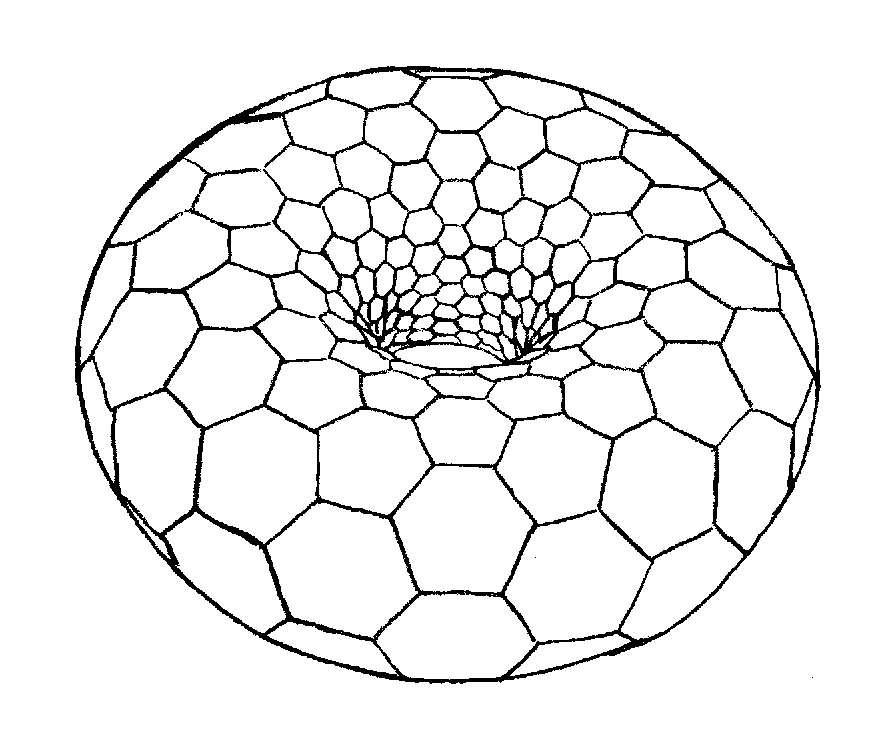
\(\chi =\left\lfloor{\frac{7+\sqrt{1+48g}}{2}}\right\rfloor\)Par exemple, \(\chi=7\) pour \(g=1\), cas illustré ci-contre (un tore – de genre 1 – vu de dessus colorié avec une carte complète à 7 régions).
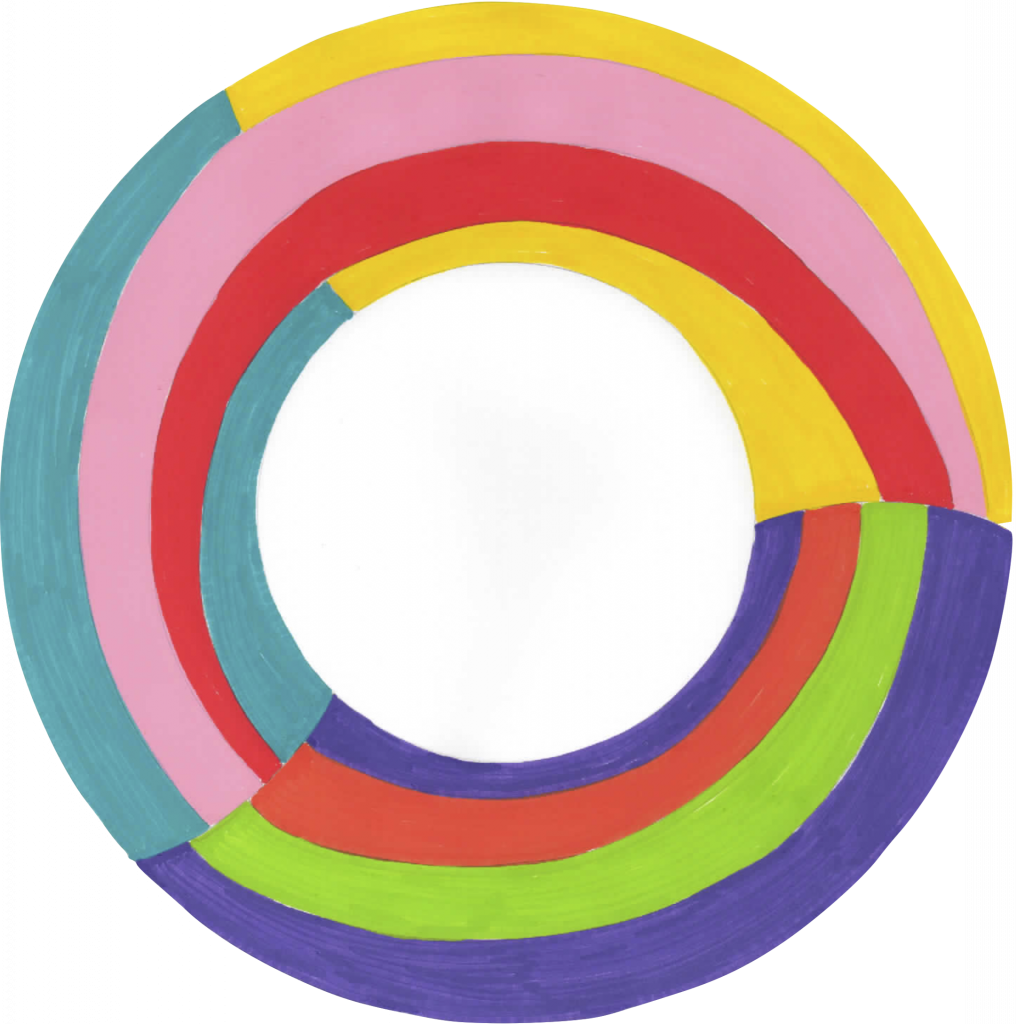
- Signifie que:
- toute carte sur une surface orientable de genre \(g\) peut être coloriée avec au plus \(\chi\) couleurs de sorte que pour toute paire de régions frontalières, celles-ci soient de couleurs différentes,
- il existe des cartes nécessitant \(\chi\) couleurs, et plus précisément des cartes complètes à \(\chi\) régions, c’est-à-dire dont toutes les régions sont frontalières les unes des autres.
- Prouvée en 1891 par Lothar Heffter pour \(g\) compris entre 1 et 7, en exhibant des tableaux d’adjacence de cartes complètes à \(\chi\) couleurs, c’est-à-dire à exactement \(\chi\) régions toutes frontalières les unes des autres, en 1968 par Gerhard Ringel & Ted Youngs pour tout genre au moins égal à 1, en 1978 par Kenneth Appel et Wolfgang Haken en genre 0 (théorème des quatre couleurs).
- Racontée par Saul Stahl, The Other Map Coloring Theorem, Mathematics Magazine, May, 1985, Vol. 58, No. 3.
Formule d’Euler pour les polyèdres
Relie le nombre \(f\) de faces, le nombre \(s\) de sommets et le nombre \(a\) d’arêtes d’un polyèdre.
Lorsque celui-ci est convexe, ou tracé sur une surface orientable de genre nul, la formule est:
\( s + f – a =2\)Par exemple, un ballon de foot ordinaire est composé de \(f = 32\) faces (20 hexagones, 12 pentagones), \(s = 60\) sommets et \(a = 90\) arêtes.

- De nombreuses preuves existent. On peut en trouver 21 sur cette page en anglais.
- Se généralise aux polyèdres tracés sur une surface orientable de genre \(g\) en:
Par exemple, un tore de genre \(g =1\) peut être pavé avec des hexagones, contrairement à la sphère, et l’on a \(s=6 \times f/3 = 2 f\), \(a=6 \times f/2 = 3f\), \(s + f – a =2f + f – 3 f = 0 = 2 – 2 \times 1 = 2 – 2 g.\)