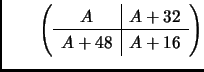Matrices et tableaux

Une matrice peut être entrée directement, en ligne, en séparant les éléments d'une ligne par un blanc ou une virgule. Un point virgule permet de séparer deux lignes.
ex : $\mathtt{A}=[16\ 3\ 2\ 13;\ 5\ 10\ 11\ 8;\ 9\ 6\ 7\ 12;\ 4\ 15\ 14\ 1]$

sum(A) : vecteur-ligne, somme des colonnes de A.
A' : transposée de A.
sum(A')' : vecteur-colonne, somme des lignes de A.
diag(A) : vecteur-colonne des éléments diagonaux de A.
A(i,j) : élément de A sur la i-ième ligne et j-ième colonne.
A(8) : élément de A, situé en 8-ième position quand on lit en descendant les colonnes (ici, A(8)=15).

Matlab adapte la taille de la matrice suivant les besoins. Par exemple,

$$\left\{\begin{array}{l} \mathtt{X=A};\\ \mathtt{X(4,5)=17} \end{array} \right.$$   donne$$\qquad X=\left( \begin{array}{ccccc} 16&3&2&13 & 0\\ 5 &10&11&8 & 0\\ 9&6&7&12& 0\\ 4&15&14&1& 17 \end{array}\right)$$

On peut utiliser les :pour gagner du temps.
1:10 est la suite (1,2,...,10).
0:pi/4:pi est la suite $(0,\pi/4,\pi/2,3\pi/4,\pi)$.
A(1:k,j) donne les k premiers éléments de la j-ième colonne de la matrice A.
: signifie tous les éléments.
end signifie le dernier élément.
sum(A(:,end))=sum(A(1:4,4)) calcule la somme de tous les éléments de la quatrième colonne de A.

Pour fabriquer des matrices, on peut utiliser (entre autres) ces 3 commandes :
zeros(i,j) génère une matrice $i\times j$ de 0,
ones(i,j) génère une matrice de taille $i\times j$ de 1,
rand(i,j) génère une matrice $i\times j$ de nombres uniformément répartis sur [0,1].

Ces constructions sont à utiliser sans modération, car préallouer de la place pour un tableau avant de le remplir fait gagner du temps.

On peut aussi construire des matrices par concaténation (par blocs) :

$$\mathtt{B=[A\ A+32;\ A+48\ A+16]}$$   donne$$\qquad \left(\begin{array}{c\vert c} A & A+32\\ \hline A+48 & A+16 \end{array}\right)$$

Opérations sur les matrices :
- somme de deux matrices : A+B
- produit de deux matrices (suivant les règles du calcul matriciel) : A*B
- multiplication terme à terme : A.*B
- calcul du déterminant, de l'inverse, du vecteur des valeurs propres, du polynôme caractéristique : det, inv, eig, poly
- extraction d'éléments d'une matrice : A(cond(A)).
Par exemple, A(A>=0) extrait les éléments positifs de A,
A(isprime(A)) extrait les éléments premiers de A,
A($\sim$isprime(A)) extrait les éléments qui ne sont pas premiers de A,
Une autre manière d'arriver à de tels résultats : k=find(isprime(A)) est le vecteur des numéros des éléments premiers de A. Puis A(k) donne les éléments premiers de A.