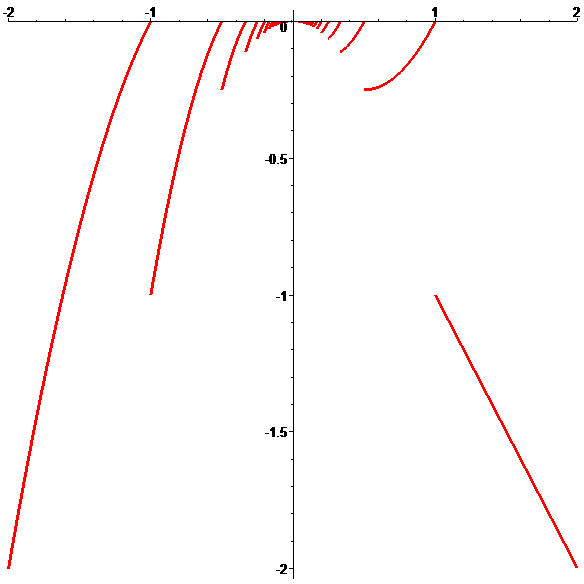\(\color{blue}\vphantom{()_p} f(x)=x\,\mathsf{E}(1/x)-1\)

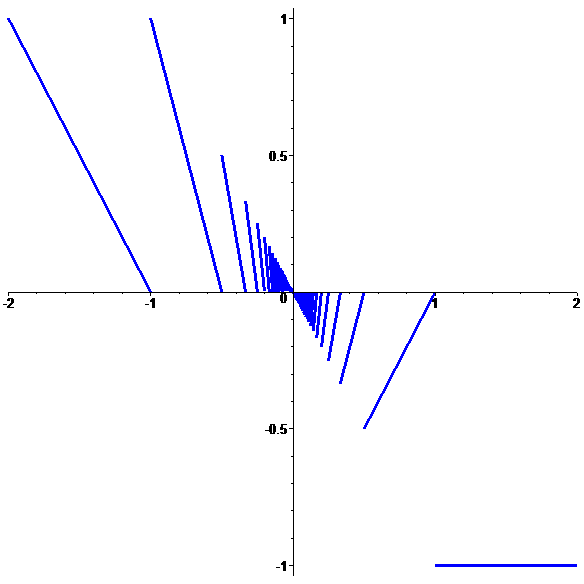
Graphe de \(\color{blue}f\)

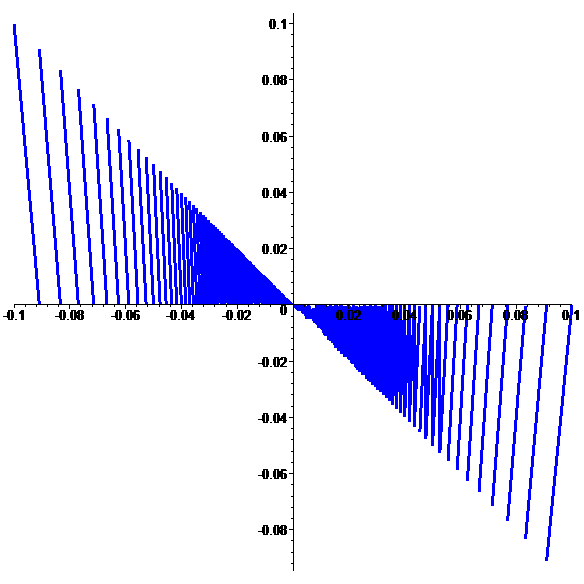
Graphe de \(\color{blue}f\) (zoom)

\(\color{blue}|f(x)|\leqslant|x|\)

En posant \(\color{blue}f(0)=0\)
\(\color{blue}f\) est continue en 0
mais continue sur aucun voisinage de 0…

 \(\color{red}\vphantom{()_p} g(x)=x^2\,\mathsf{E}(1/x)-x\)

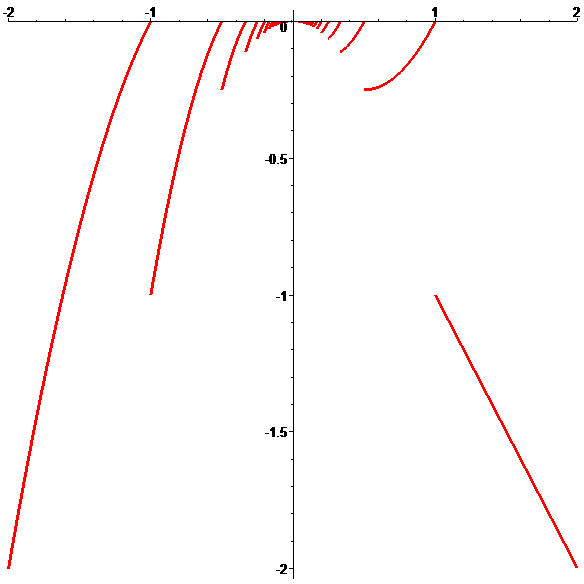
Graphe de \(\color{red}g\)

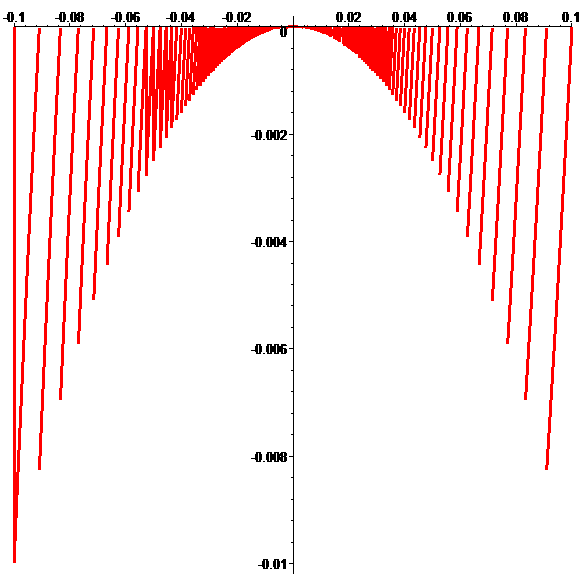
Graphe de \(\color{red}g\) (zoom)

\(\color{red}|g(x)|\leqslant x^2\)

En posant \(\color{red}g(0)=0\)
\(\color{red}g\) est dérivable en 0 \(\textbf{(}{\color{red}g'(0)=0}\textbf{)}\)
mais continue sur aucun voisinage de 0…

admettant un maximum global en 0 \(\textbf{(}{\color{red}g(0)\leqslant0}\textbf{)}\)
mais monotone sur aucun voisinage de 0…