| II. Du côté de sin(1/x )… |
Avec \(\vphantom{()_p} \sin(1/x)\)…
| \(\color{blue}f(x) =\sin(1/x)\) |
\(\color{red}g(x) = x\sin(1/x)\) |
| \(\color{lime}h(x) = x^2\sin(1/x)\) |
\(\color{magenta}k(x) = x^3\sin(1/x)\) |
| \(\color{cyan}l(x) = x^4\sin(1/x)\) |
\(\color{yellow}m(x) = x^5\sin(1/x)\) |
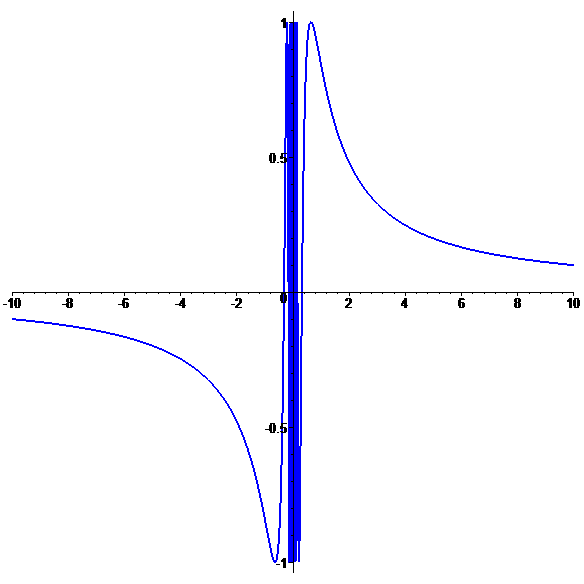
Graphe de \(\color{blue}f\)
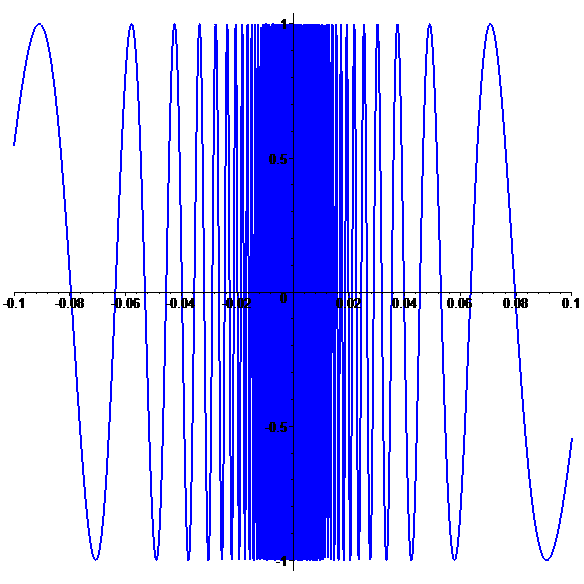
Graphe de \(\color{blue}f\) (zoom)
\(\color{blue}f\) n'est pas prolongeable
par continuité en 0
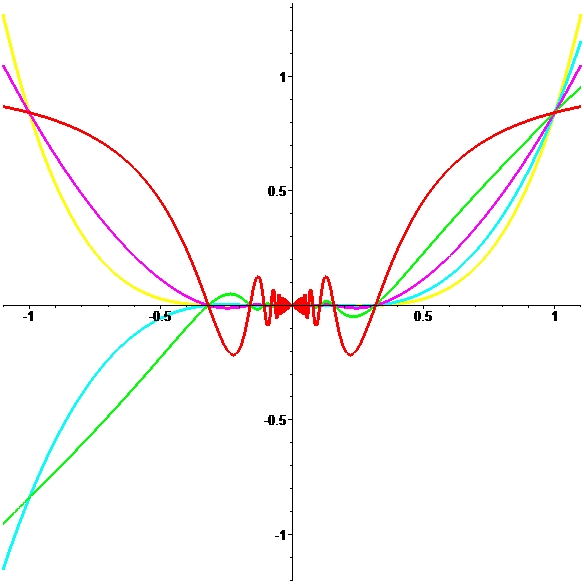
Graphes de \({\color{red}g},{\color{lime}h},{\color{magenta}k},{\color{cyan}l},{\color{yellow}m}\)
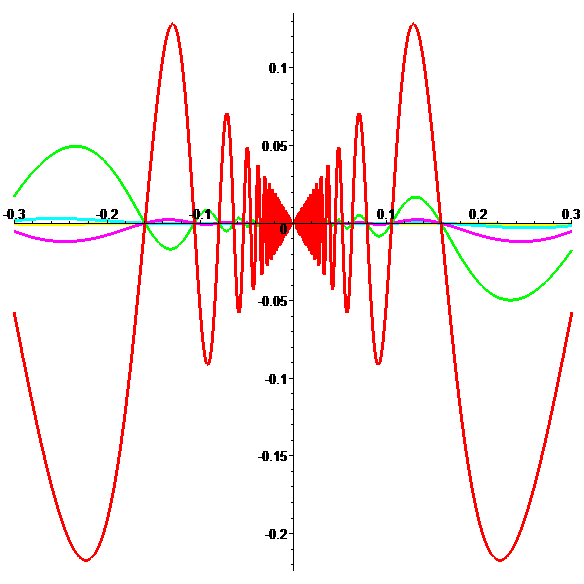
Graphes de \({\color{red}g},{\color{lime}h},{\color{magenta}k},{\color{cyan}l},{\color{yellow}m}\) (zoom)
\(\color{red}|g(x)|\leqslant|x|\)
En posant \(\color{red}g(0)=0\)
\(\color{red}g\) est continue en 0 mais pas dérivable
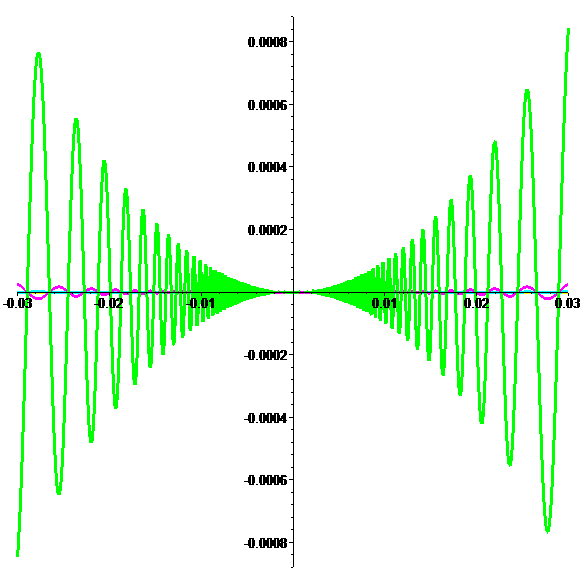
Graphes de \({\color{lime}h},{\color{magenta}k},{\color{cyan}l},{\color{yellow}m}\) (méga-zoom)
\(\color{lime}|h(x)|\leqslant x^2\) et \(\color{magenta}|k(x)|\leqslant|x|^3\)
En posant \(\color{lime}h(0)=0\) et \(\color{magenta}k(0)=0\)
\(\color{lime}h\) est dérivable en 0 mais pas C1
\(\color{magenta}k\) est C1 en 0
mais pas deux fois dérivable
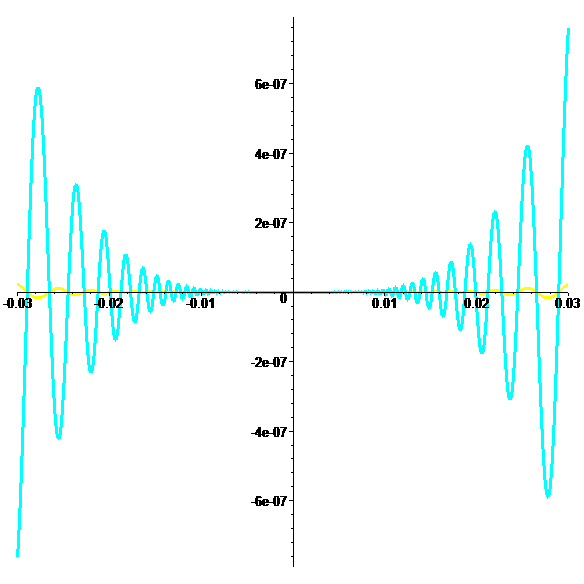
Graphes de \({\color{cyan}l},\color{yellow}m\) (giga-zoom)
\(\color{cyan}|l(x)|\leqslant x^4\) et \(\color{yellow}|m(x)|\leqslant |x|^5\)
En posant \(\color{cyan}l(0)=0\) et \(\color{yellow}m(0)=0\)
\(\color{cyan}l\) est deux dérivable en 0 mais pas C2
\(\color{yellow}m\) est C2 en 0 mais pas trois fois dérivable
Avec \(\vphantom{()_p} \sin^2(1/x)\)…
| \(\color{blue}\varphi(x)=x^4\sin^2(1/x)\)
| \(\color{red}\psi(x)=x^5\sin^2(1/x)\)
|
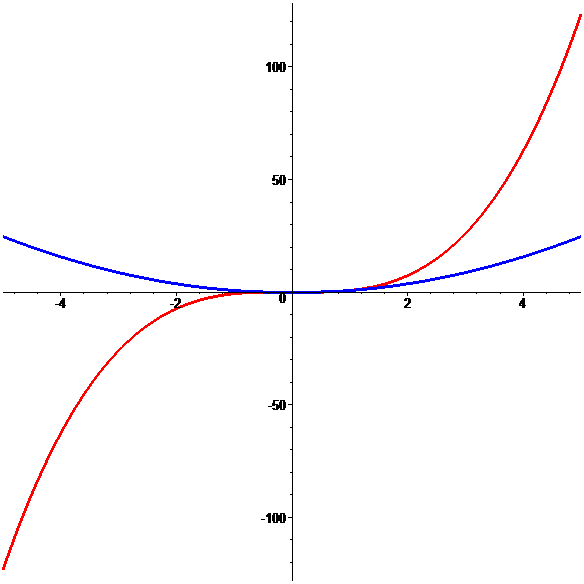
Graphes de \({\color{blue}\varphi},\color{red}\psi\)
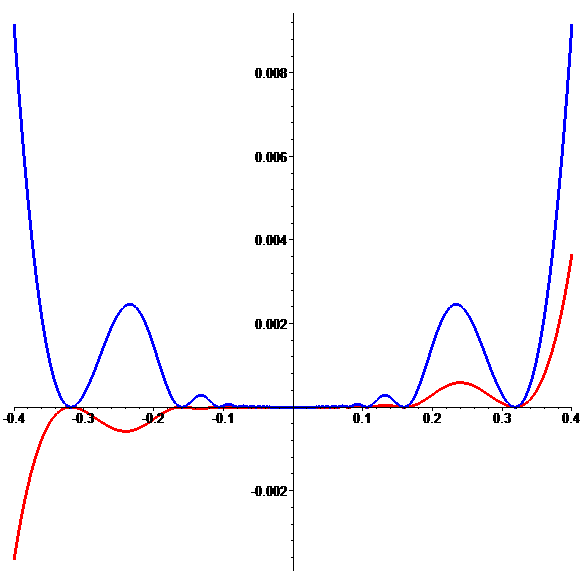
Graphes de \({\color{blue}\varphi},\color{red}\psi\) (zoom)
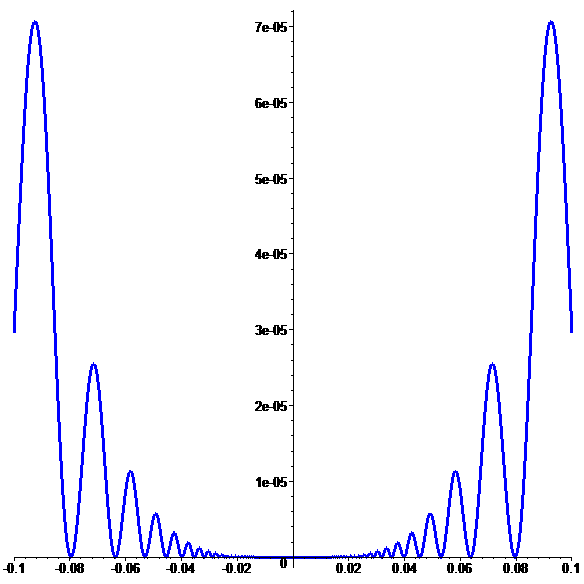
Graphe de \(\color{blue}\varphi\) (méga-zoom)
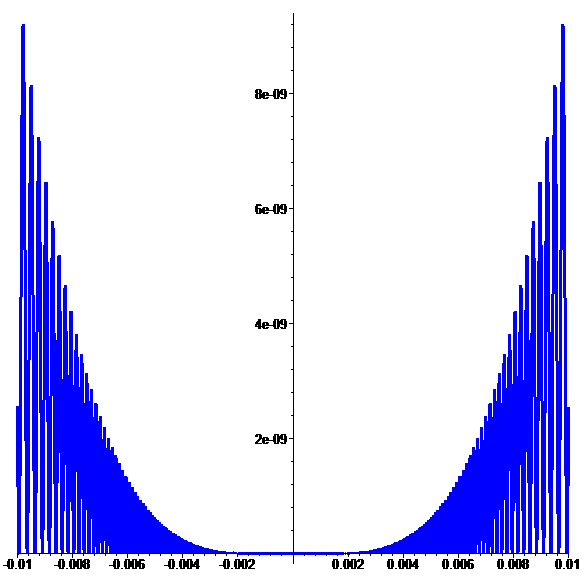
Graphe de \(\color{blue}\varphi\) (giga-zoom)
En posant \(\color{blue}\varphi(0)=0\),
\(\color{blue}\varphi\) est C1 en 0
admettant un minimum global en 0 \(\textbf{(}{\color{blue}\varphi(x)\geqslant0}\textbf{)}\)
mais monotone sur aucun voisinage de 0…
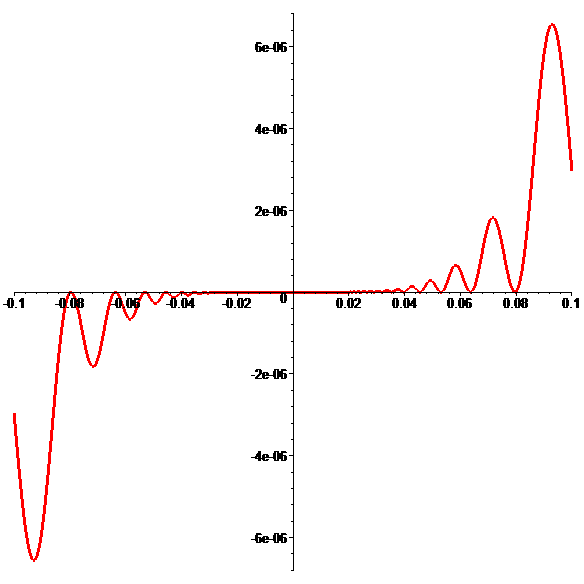
Graphe de \(\color{red}\psi\) (méga-zoom)
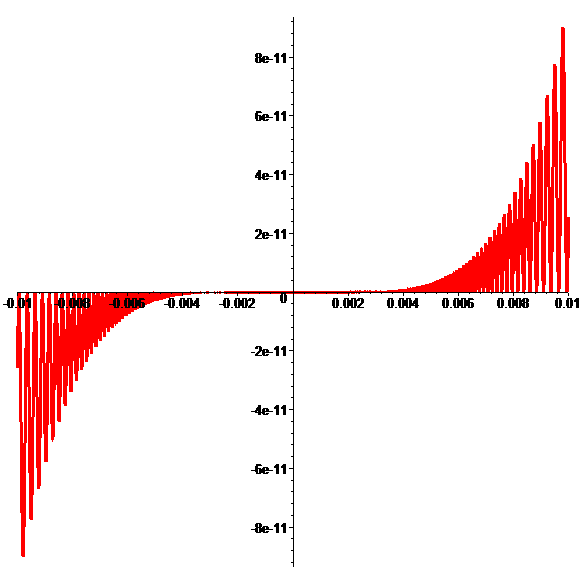
Graphe de \(\color{red}\psi\) (giga-zoom)
En posant \(\color{red}\psi(0)=0\),
\(\color{red}\psi\) est C2 en 0
de courbe traversant sa tangente en 0
\(\textbf{(}\color{red}\psi(x)\leqslant0\) pour \(x\leqslant0\)
et \(\color{red}\psi(x)\geqslant0\) pour \(x\geqslant0\textbf{)}\)
mais n'admettant pas de point d'inflexion en 0…












