Avec les deux fonctions tangentes…

Graphes de \(\color{blue}f\) et \(\color{red}g\)

\(\vphantom{\frac{a}{a}}\)Composition de \(\color{blue}f\) et \(\color{red}g\)

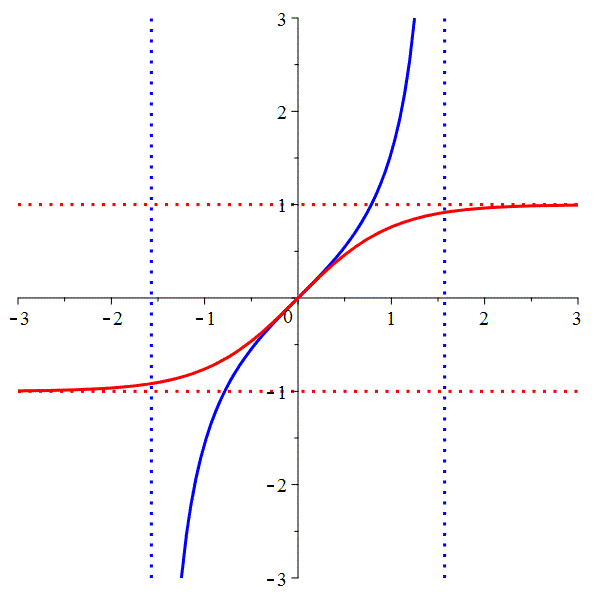
Posons \({\color{lime}\varphi}={\color{red}g}\boldsymbol{\circ} {\color{blue}f}: \mathopen]-\frac{\pi}{2},\frac{\pi}{2}\mathclose[\longrightarrow\mathopen]-1,1[\)

Graphe de \(\color{lime}\varphi\)

On prolonge \(\color{lime}\varphi\) par continuité en \(-\frac{\pi}{2}\) et \(\frac{\pi}{2}\)
en posant \(\color{lime}\varphi(-\frac{\pi}{2})=\varphi(\frac{\pi}{2})=0.\)

« Normalisons » \(\color{lime}\varphi\) à l'aide de \({\color{magenta}\psi}(x)=\frac12\big[{\color{lime}\varphi}\big(\pi(x-\frac12)\big)+1\big]:\)

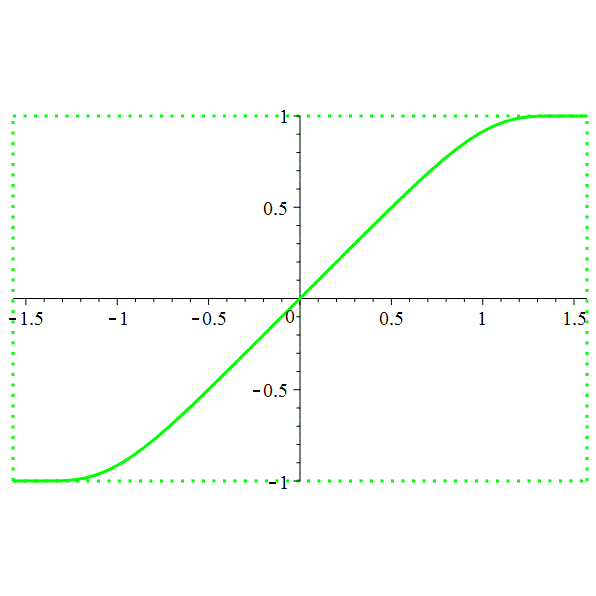
\(\color{magenta}\left\{\begin{array}{l}\vphantom{\frac{b^b}{q}} \psi:[0,1]\longrightarrow[0,1] \\ \psi(x)=\dfrac{1}{\mathrm{e}^{2\cot(\pi x)}+1} \;\text{ si }\; x\!\in\!\mathopen]0,1[ \\[0.5ex] \psi(0)=0 \;\text{ et }\; \psi(1)=1 \end{array}\right.\)




Graphe de \(\color{magenta}\psi\)

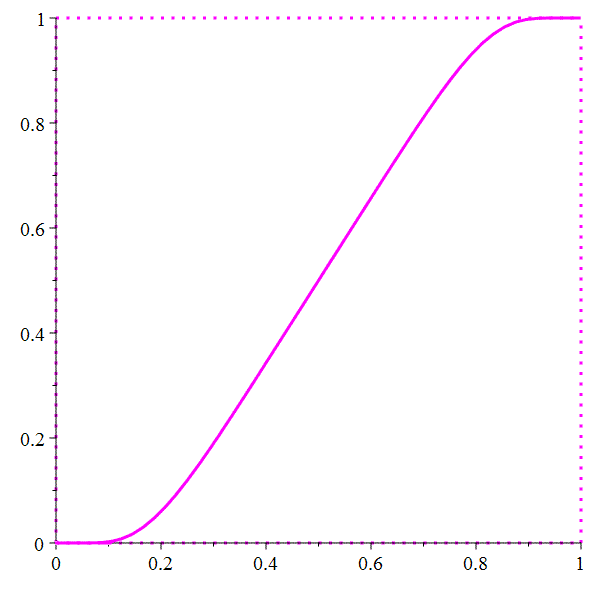
\(\color{magenta}\forall n\!\in\!\mathbb{N}^*,\;\psi^{\lower 1ex{(n)}}(0)=\psi^{\lower 1ex{(n)}}(1)=0\)

Prolongement aux extrémités :
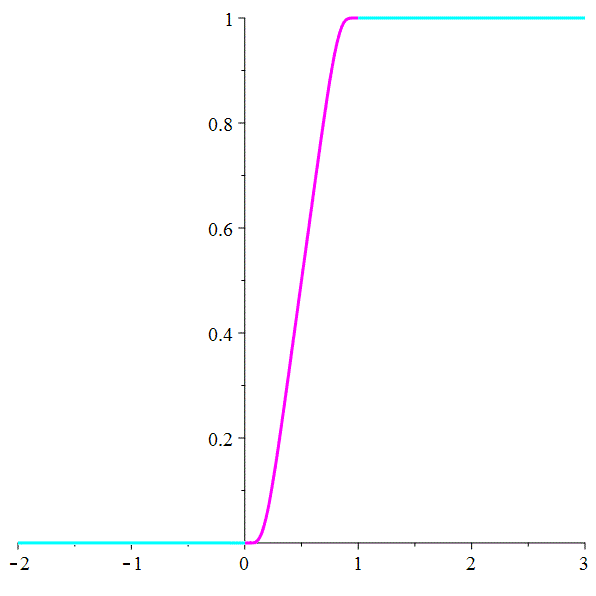
\(\color{cyan}\left\{\begin{array}{c}\vphantom{\frac{b^b}{q}} \hat{\psi}:\mathbb{R}\longrightarrow[0,1] \\ \hat{\psi}(x)=0 \text{ si } x\leqslant 0 \\ \hat{\psi}(x)=1 \text{ si } x\geqslant 1 \end{array}\right.\)

Graphe de \(\color{cyan}\hat{\psi}\)

Une fonction de classe C^\(\infty\) sur \(\mathbb{R}\)
reliant deux demi-droites…