-

Aimé Lachal Dérivabilité – Non dérivabilité Les premiers monstres de l'analyse…
 |
(1845–1918) Mathématicien allemand |
| \(f_0(x)\!=\!\frac12\; \text{ si } x\!\in\![0,1]\) |
| \(f_{n+1}(x)\!=\!\begin{cases} \vphantom{\dfrac{b}{a}}\frac12 f_n(3x) & \text{si } x\!\in\![0,\!\frac13]\\[-1ex] \frac12 & \text{si } x\!\in\![\frac13,\!\frac23]\\ \frac12 f_n(3x\!-\!2) \!+\! \frac12 & \text{si } x\!\in\![\frac23,1] \end{cases}\) |
| \(\displaystyle f \!=\!\!\lim_{n\to\infty}f_n\) |
 |
| Bernard Bolzano (1781–1848) |
| \(f_0(x)\!=\!x \;\text{ si } x\!\in\![0,1]\) |
| \(f_{n+1}(x)\!=\!\begin{cases} \vphantom{\dfrac{b}{a}}\frac23 f_n(3x) & \text{si } x\!\in\![0,\!\frac13]\\[-1ex] \frac23\!-\!\frac13 f_n(3x\!-\!1)& \text{si } x\!\in\![\frac13,\!\frac23]\\ \frac23 f_n(3x\!-\!2) \!+\! \frac13 & \text{si } x\!\in\![\frac23,1] \end{cases}\) |
| \(\displaystyle f \!=\!\!\lim_{n\to\infty}f_n\) |
 |
(1870–1924) Mathématicien suédois |
|
 |
(1826–1866) Mathématicien allemand |
| \(\begin{array}{rl} f(x)\hspace{-1em}&=\displaystyle\sum_{k=1}^{\infty} \frac{1}{k^2}\sin(k^2x)\\ &=\displaystyle\sin(x)\!+\!\tfrac14 \sin(4x)\!+\!\tfrac19 \sin(9x)\!+\!\cdots \end{array}\) |
 |
(1815–1897) Mathématicien allemand |
| \(\begin{array}{rl} f(x)\hspace{-1em}&=\displaystyle\sum_{k=0}^{\infty} \frac{1}{2^k}\sin(3^kx)\\ &=\displaystyle\sin(x)\!+\!\tfrac12 \sin(3x)\!+\!\tfrac14 \sin(9x)\!+\!\cdots \end{array}\) |
 |
| Teiji Takagi (1875–1960) Mathématicien japonais |
|
| Lin Wen (Contemporain) Mathématicien chinois |
| \(\begin{array}{rl} f(x)\hspace{-1em}&=\displaystyle\prod_{k=0}^{\infty} \left[1+\frac{1}{2^k}\sin(6^{k(k+1)/2}x)\right]\\ &=\big[1\!+\!\sin(x)\big]\big[1\!+\!\tfrac12\sin(6^3x)\big]\big[1\!+\!\tfrac14\sin(6^6x)\big]\!\cdots \end{array}\) |
| Quelques citations |
 |
 |
 |
| Robert Brown (1773–1858) Botaniste écossais | ||
|
|
 |
 |
|
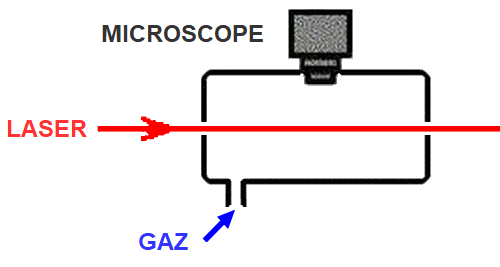
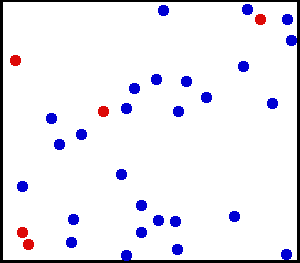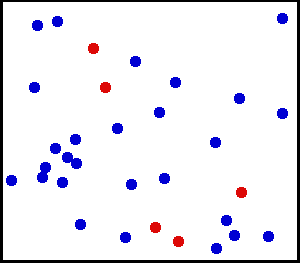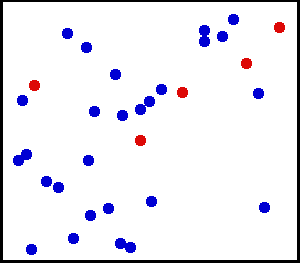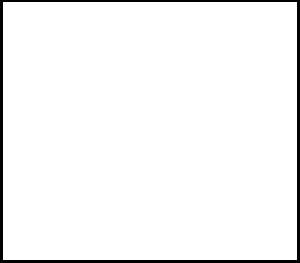
Le mouvement désordonné et lent d'une grosse particule, grain de poussière ici,
observable au microscope dans un gaz (fumée), est dû aux chocs des petites particules,
atomes ou molécules du gaz, qui, elles, ne sont pas vues au microscope.
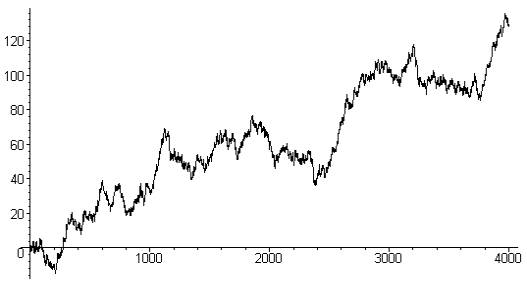
Si le mouvement du grain de poussière est désordonné, alors celui des atomes ou molécules de gaz l'est aussi. Ce mouvement aléatoire et erratique d'un gaz est appelé mouvement brownien. |
|
 |
 |
 |
|
|
| |
 |
 |
 |
| Albert Einstein (1879–1955) Physicien allemand | ||
 |
| Divers contributeurs |
 |
 |
 |
 |
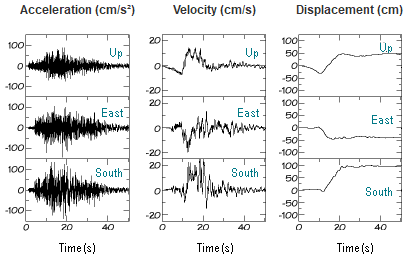 | |
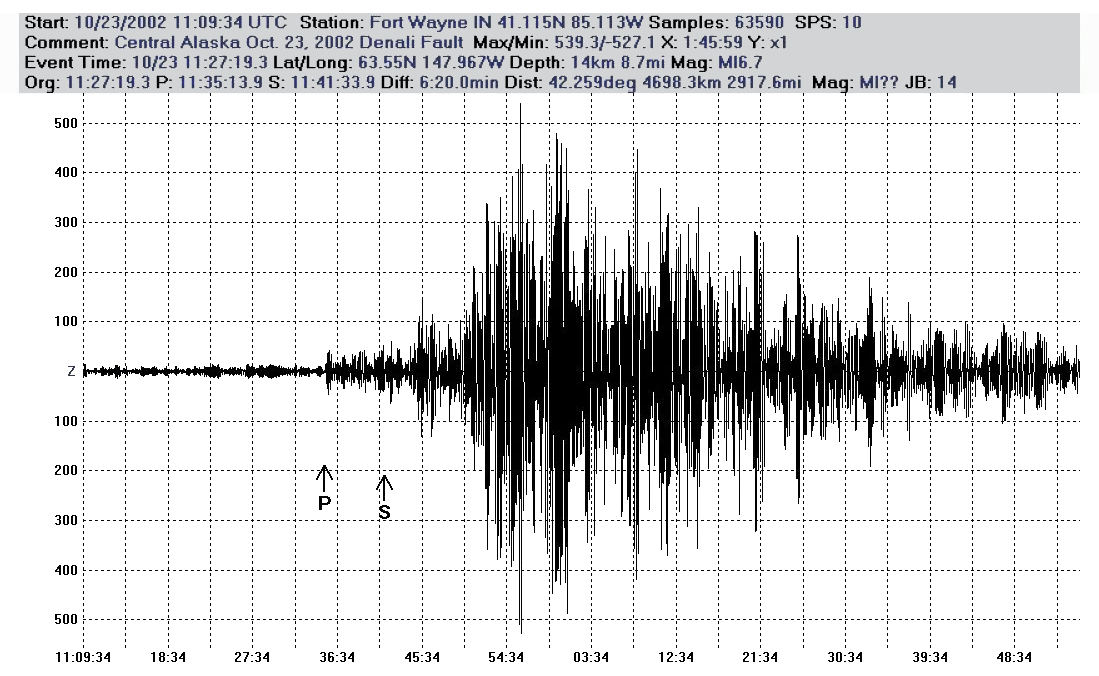
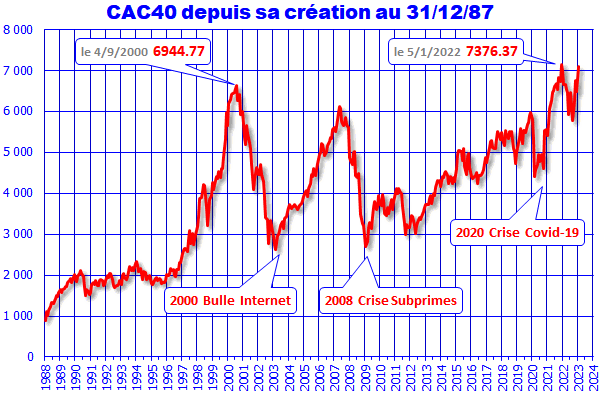
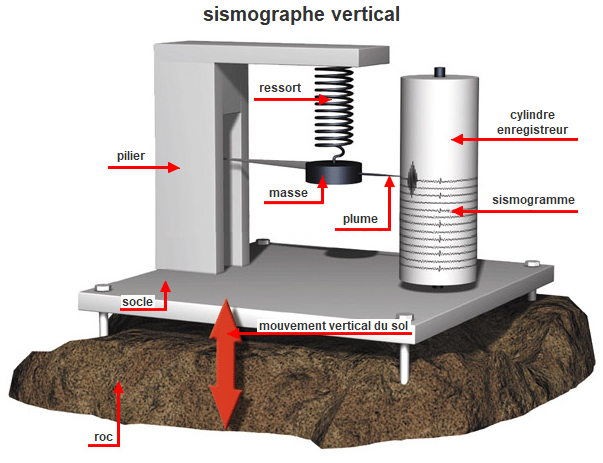
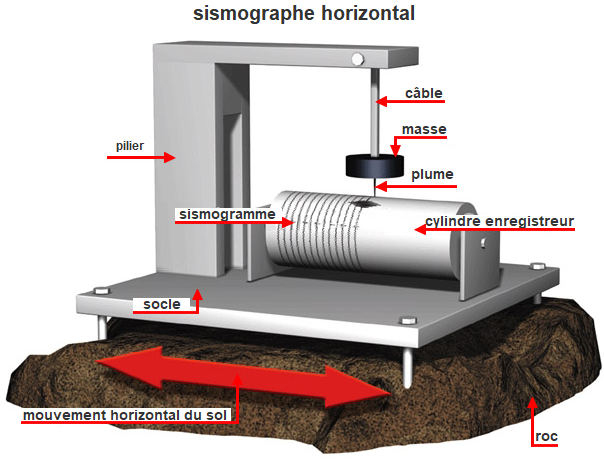
Séisme |
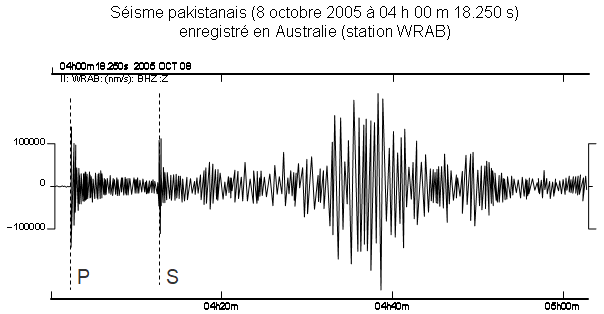
Séisme |
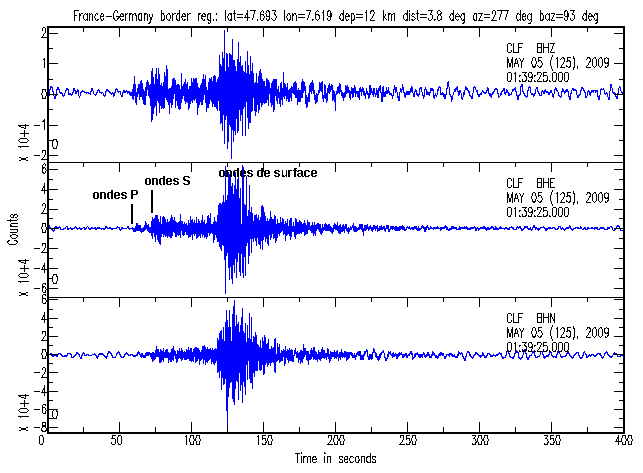
Séisme |
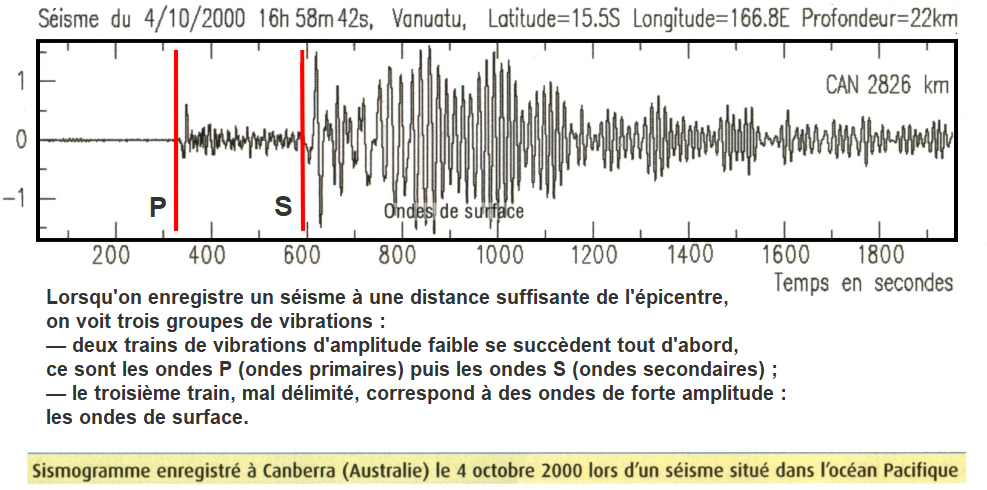
Séisme |
| ◄ | Sommaire | ► |