| VI. Un contre-exemple de la règle de L'Hôpital |
 |
| Guillaume François Antoine de L'Hôpital |
| (1661-1704) |
| Mathématicien français |
Règle de L'Hôpital
Hypothèses : soit \(f\) et \(g\) des fonctions
définies sur l'intervalle
\([x_0\!-\!\varepsilon,x_0\!+\!\varepsilon]\) \(\textbf{(}\varepsilon>0\textbf{)}\)
telles que :
- \(f(x_0)=g(x_0)=0\,;\)
- \(f\) et \(g\) continues en \(x_0\,;\)
- \(f\) et \(g\) dérivables sur
\([x_0\!-\!\varepsilon,x_0\mathclose[\cup\mathopen]x_0,x_0\!+\!\varepsilon]\,;\)
- \(g'\) ne s'annule pas sur \([x_0\!-\!\varepsilon,x_0\mathclose[\cup\mathopen]x_0,x_0\!+\!\varepsilon].\)
On a affaire à la forme indéterminée
\(\displaystyle\lim_{x\to x_0}\frac{f(x)}{g(x)}=\frac{0}{0}.\)
|
Si \(\displaystyle\lim_{x\to x_0}\frac{f'(x)}{g'(x)}=\ell\!\in\hspace{-0.2em}\overline{\mathbb{R}},\)
alors \(\displaystyle\lim_{x\to x_0}\frac{f(x)}{g(x)}=\ell.\)
|
La règle reste valable lorsque \(x_0=\pm\infty,\)
ou \(\displaystyle\lim_{x\to x_0}f(x_0)=\displaystyle\lim_{x\to x_0}g(x_0)=\pm\infty.\)
Contre-exemple
Au voisinage de \(+\infty\)
| \(\color{red}\,f(x)\!=\!x\!+\!\cos(x)\sin(x)\,\) |
\(\color{lime}\,g(x)\!=\!f(x) \mathrm{e}^{\frac{1}{10}\sin(x)}\,\) |
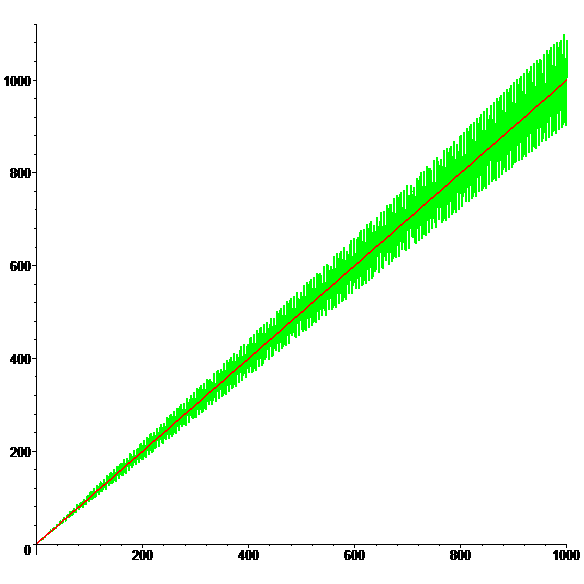
Graphes de \(\color{red}f\) et \(\color{lime}g\)
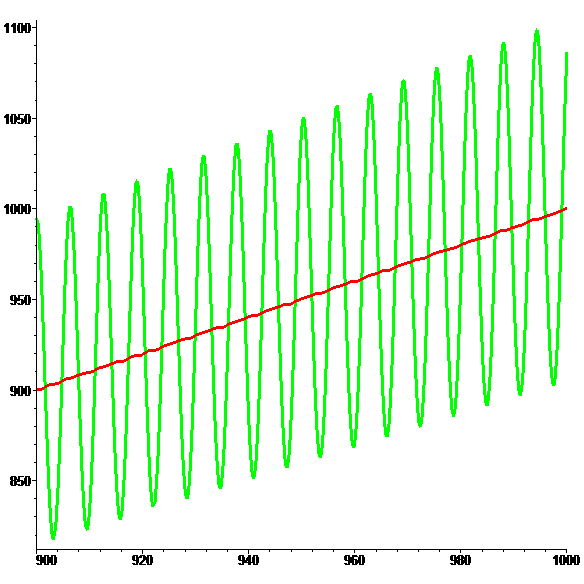
Graphes de \(\color{red}f\) et \(\color{lime}g\) (zoom)
FAIT :
\(\displaystyle\lim_{x\to+\infty}\frac{\color{red}f(x)}{\color{lime}g(x)}=\frac{\color{red}\infty}{\color{lime}\infty}\)
ICI N'EXISTE PAS ET
\(\displaystyle\lim_{x\to+\infty}\frac{\color{red}f'(x)}{\color{lime}g'(x)} =0\) |
Explication
\(\begin{array}{rl}
\color{red}f'(x)\!\!\!\!\!&\!\color{red}=2\cos^2(x)\\
\color{lime}g'(x)\!\!\!\!\!&\!\color{lime}=\frac{1}{10} \cos(x)\big[x\!+\!\cos(x)(\sin(x)\!+\!20)\big]\mathrm{e}^{\frac{1}{10}\sin(x)}
\end{array}\)
Les dérivées \(\color{red}f'\) et \(\color{lime}g'\) s'annulent
une infinité de fois
au voisinage de \(+\infty\text{...}\)
Transcription au voisinage de 0
Avec le changement de variable de l'infini en 0 \((x\mapsto 1/x):\)
\(\color{red}\varphi(x)=\dfrac{1}{f(\frac1x)}\qquad\color{lime}\psi(x)=\dfrac{1}{g(\frac1x)}\)
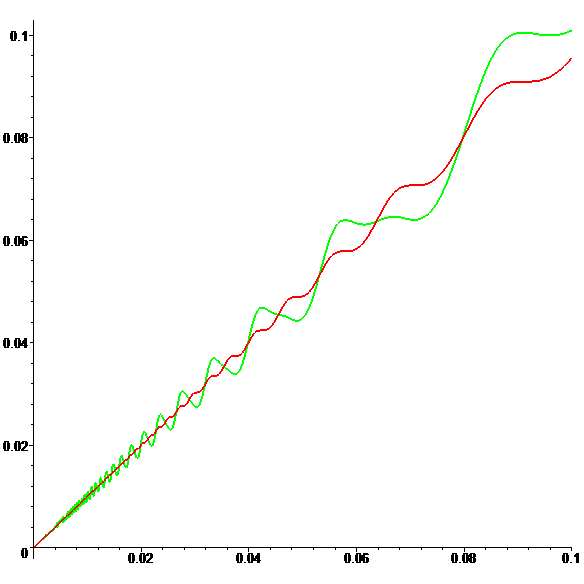
Graphes de \(\color{red}\varphi\) et \(\color{lime}\psi\)
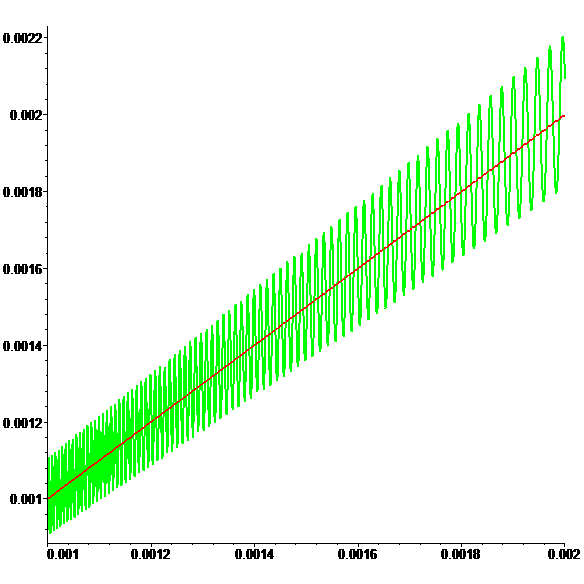
Graphes de \(\color{red}\varphi\) et \(\color{lime}\psi\) (zoom)
FAIT :
\(\displaystyle\lim_{x\to 0}\dfrac{\color{red}\varphi(x)}{\color{lime}\psi(x)}=\dfrac{\color{red}0}{\color{lime}0}\)
ICI N'EXISTE PAS ET
\(\displaystyle\lim_{x\to 0}\dfrac{\color{red}\varphi'(x)}{\color{lime}\psi'(x)}=0\) |





