POLE DE MATHÉMATIQUES

Code de calcul ELVIS Fluides visco-élastiques dans des écoulements de faible épaisseur

INSTITUT CAMILLE JORDAN

Contexte :

Les équations de Stokes-Oldroyd-B permettent de modéliser des écoulements visco-élastiques. Les non-linéarités introduites par les propriétés rhéologiques de ces fluides non-newtoniens se traduisent numériquement par de grandes difficultés pour le calcul direct d'écoulements 3D. Les effets d'échelles en mécanique des films minces induisent des difficultés encore plus grandes, mais une analyse asymptotique rigoureuse permet de construire un système limite équivalent dont le traitement numérique est plus facile. Après avoir proposé et justifié le modèle asymptotique (hypothèse de film mince), nous avons proposé et analysé une méthode numérique permettant de calculer la solution. Ce travail est adapté à l'étude d'écoulements visco-élastiques de faible épaisseur à partir i.) du modèle d'Oldroyd-B, ii.) du modèle de Phan-Thien Tanner (avec correction d'ordre 1 dans le modèle asymptotique).

Algorithme :

La méthode de calculs est basée sur une discrétisation par différences finies et un algorithme de point fixe qui permet d'augmenter progressivement la non-linéarité. Chaque étape du point fixe (de nature newtonienne) est résolue par une méthode d'Uzawa en traitant le champs des vitesses comme inconnue principale (contrairement à la résolution usuelle du problème newtonien, qui traite la pression comme inconnue principale en résolvant l'équation de Reynolds). Cet algorithme permet de déterminer les champs de pression, vitesse, tenseur de contraintes (visqueux et élastique) et la viscosité effective pour des écoulements 3D sous l'hypothèse de film mince.

Programmation :

Le programme, implanté en Fortran 95, est constitué de deux versions commentées, permettant de prendre en compte des conditions aux limites réalistes du point de vue des applications en mécanique : la version (A) est adaptée à une alimentation en pression ; la version (B) correspond à une alimentation en débit. Le code est disponible sur simple demande.

Auteurs :

Laurent Chupin (Lyon) & Sébastien Martin (Orsay).

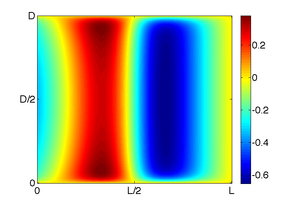
Illustrations numériques :

• Fig. 1 : Pression hydrodynamique, contrainte de cisaillement et viscosité effective dans un écoulement lubrifié visco-élastique, pour un profil linéaire convergeant avec alimentation en pression, un paramètre de retard r=0.7 et un nombre de Deborah De=0.5.

• Fig. 2 : Influence du paramètre de retard sur la pression dans un profil convergeant-divergeant avec alimentation en débit : r=0 (cas newtonien), r=0.5, r=0.7. Cette simulation invalide l'approximation du palier infiniment long dans le cas non-newtonien.