Blog of Raphael Ducatez

Il est toujours mal aisé de parler de prédiction économique voir même simplement de modélisation tant le monde réel est compliqué. Ici je présente trois petit modèle très simple avec chaque fois un petit théorème. On peut plutôt parler de «fables» : des histoires très simplistes qui illustre le propos plutôt qu'une argumentation et avec peut-être une morale à fin.

L'algorithme hongrois, un argument neo-liberal ?

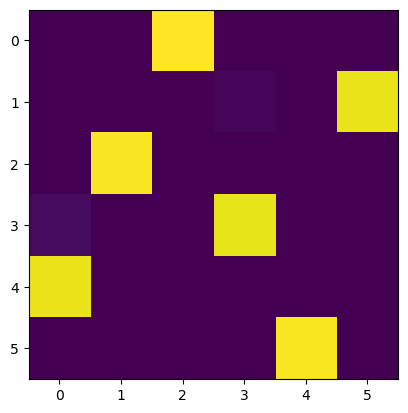
Considérons un tableau N par N avec des entrées positives et choisissons N cases de telle sorte qu'il y en ait exactement une sur chaque ligne et chaque colonne. Comment trouver la configuration qui minimise la somme des cases choisies ? Il y a plusieurs illustrations/motivation à ce problème. Par exemple, on peut penser à un ensemble de travailleurs ayant des compétences différentes et une liste de taches à réaliser. On aimerait alors donner une répartition des taches qui correspond au mieux les compétences des travailleurs. 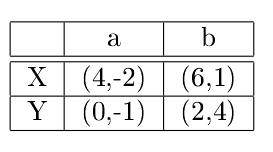\[ \text{Exemple : }\left(\begin{array}{cccc} 1 & 4 & \boxed{2} & 3\\ \boxed{1} & 5 & 6 & 4\\ 7 & \boxed{2} & 2 & 1\\ 3 & 4 & 3 & \boxed{1} \end{array}\right)\quad\text{Somme minimale}=6. \] Bien sur il est possible ici de tester toutes les possibilités mais ce nomble devient vite trop important lorsque le tableau est un peu grand. Le but du jeu est donc de trouver un algorithme efficace. L'idée de l'algorithme hongrois repose sur les deux observations suivantes:

• Si il est possible de choisir une configuration uniquement avec des cases de valeur nulle alors c'est terminé et le cout total est nul.
• Si on modifie le tableau en ajoutant une même valeur sur toute une ligne ou sur tout une colonne alors on obtient un problème équivalent \[ c(x,y)\rightarrow c(x,y)+P(x)+Q(y) \] En effet cela revient à ajouter une constante au cout total et on ne modifie donc en rien le problème de minimisation : la configuration minimale reste la même.

Le principe de l'algorithme est d'ajuster ces valeurs \(P\) et \(Q\) de manière itérative de telle sorte à obtenir suffisamment de zéro dans le tableau pour se retrouver le premier cas. Sans entrer dans le détail des différentes étapes de l'algorithme voici juste faire quelques remarques. Ce qui rend l'algorithme intéressant d'un point de vue de l'économie est qu'il semble assez similaire au mécanisme de l'offre et la demande avec une fluctuation des prix. Chaque travailleur (=ligne) commence par postuler pour la(-es) taches qui lui conviendrait le mieux et de même pour chaque tache (ligne) une proposition est envoyée au(x) travailleur(s) le mieux qualifié pour la tache. Ensuite si un travailleur reçoit plusieurs propositions il augmente légèrement ses tarifs et inversement il les diminue si il ne voit proposer aucune tache. (=augmenter ou diminuer toute une ligne) De même on augmente ou diminue de prix pour une tache si elle est très demandée ou si au contraire ne trouve pas de travailleurs (=augmenter ou diminuer toute une colonne). Au bout d'un certain temps, on aboutit à une situation où chaque travailleur a bien une tache associée.

Assouplir le problème

On peut s'intéresser à une variante ``plus souple'' du problème où on ne suppose pas que la répartion soit purement 0 ou 1 mais peut avoir une distribution continue. Formellement on a deux ensembles fini \(E,F\) et deux distributions \((\mu(x))_{x\in E}\) et \((\nu(y))_{y\in F}\) avec \(\sum_{x\in E}\mu(x)=\sum_{y\in F}\nu(y)\). On cherche à minimiser parmi toutes les distribution \(\pi\) sur \(E\times F\) le cout total donné par \[ C(\pi):=\sum_{x,y}\pi(x,y)c(x,y)\qquad\sum_{y\in E}\pi(x,y)=\mu(x),\sum_{x\in F}\pi(x,y)=\nu(y). \] Il s'agit ici d'un problème très classique qui a même plus ou moins créé tout le domaine de recherche du transport optimal. Comme exemple de motivation Il s'agit de transporter une certaine quantité de matière première initialement répartie dans différents entrepots qu'il faut transporter vers différentes usines. Ici \(\pi(x,y)\) représente la quantité de matière transportée de \(x\) à \(y\) et \(c(x,y)\) represente le cout unitaire pour ce trajet. L'astuce ici est de relacher la condition sur \(\pi\) que toutes les et de la remplacer par une pénalité de paramètre \(\lambda\) \[ C(\lambda,\pi)=\sum_{x,y\in E}c(x,y)\pi(x,y)+\frac{\lambda}{2}(\sum_{x\in E}(\sum_{y\in E}\pi(x,y)-\mu(x))^{2}+\sum_{y}(\sum_{x\in E}\pi(x,y)-\nu(y)){}^{2}) \] Si la pénalité est suffisament grande on retrouve le problème initiale \[ \inf_{\pi\in{\cal T}}C(\pi)=\lim_{\lambda\rightarrow\infty}\inf_{\pi\geq0}C(\lambda,\pi) \] L'intéret cependant est que ce problème est plus facile à résoudre. On écrit la jacobienne \[ j(x,y)=\frac{\partial C(\lambda,\pi)}{\partial\pi(x,y)}=c(x,y)+\lambda(\sum_{z\in E}\pi(x,z)-\mu(x)+\sum_{z\in E}\pi(z,y)-\nu(y)) \] et on a bien ici les 2 points de l'algorithmes hongrois :

• la répartition qui minimise \(C(\lambda,\pi)\) ne remplit que les cases telles que \(j(x,y)=0\)
• \(j(x,y)=c(x,y)+P(x)+Q(y).\)

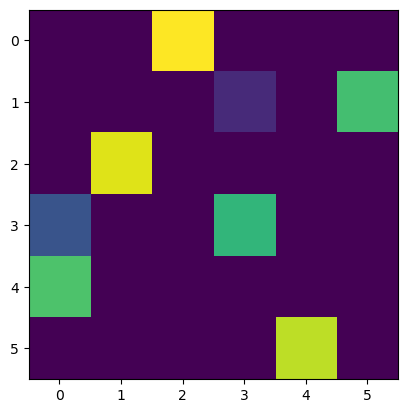
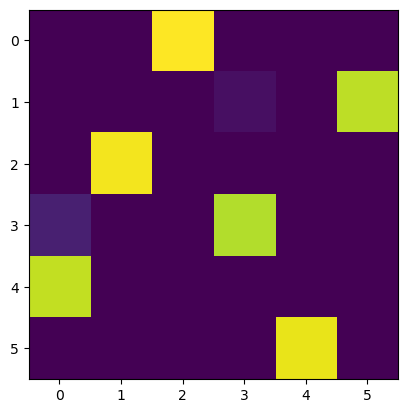
le tableau \(c\) et la distribution minimisant \(C(\lambda,\pi)\) pour \(\lambda=10,30\) et \(90\). \par\end{center} Le message de ce post est le suivant : il semble que d'une certaine manière cet algorithme est mis en pratique tous les jours de manière inconciente et que l'organisation de la société dans son ensemble repose en grande partie sur lui. Il faut reconnaitre que celui ci est assez remarquable : à la fois très simple, efficace et décentralisé.

Jeux d'argents et théorie des martingales

Dans une salle, \(N\) joueurs se réunissent et jouent au jeu d'argent suivant. À chaque temps deux joueurs sont tirés au sort et ils parient l'un contre l'autre sur un pile ou face (équilibré). La mise est fixé à \(r\times\)l'argent du joueur le pauvre avec \(0\leq r\leq 1\). Au temps long comment évolue le système ?

Une martingale

Comme le jeu est équilibré, l'argent de chaque joueur est une martingale et on a le très beau théorème «\emph{Une martingale bornée converge presque surement}». Dans le cas présent, il n'y a qu'un seul comportement assymptotique possible : tous les joueurs repartent ruinés sauf un qui rafle toute la mise.

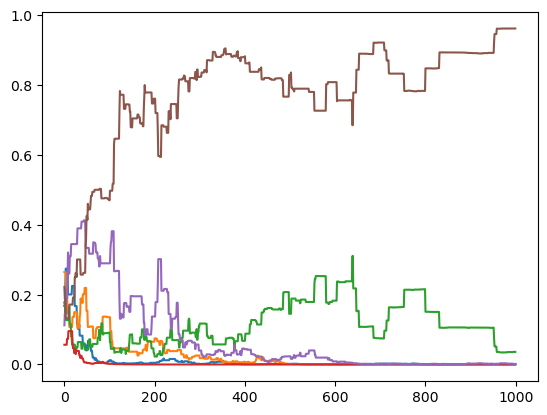
Simulation numérique avec 6 joueurs, \(p=0.3\) et quantitié total d'argent initiale égale à \(1\). De plus comme en espérance un joueur ne gagne rien ni ne perd rien, la probabilité d'être celui qui repart avec toute la mise ne dépend que de sa mise initiale \[ \text{Probabilité de gagner = }\frac{\text{argent initial}}{\text{Somme de l'argent de tous les joueurs}}. \] Ce qu'il y a de très élégant dans ce résultat c'est qu'il est en fait complètement indépendant du jeux de hazard considéré. La seule règle est que le jeu soit équitable. On peut même proposer aux joueurs de changer de jeux, de choisir leurs adversaires et leurs mises et de les laisser élaborer des «stratégies». À la fin la conclusion reste la même : un seul gagnant et avec une probabilité simplement proportionnelle à la mise initiale.

De l'inégalité parmi les hommes

Naivement on pourrait affirmer que comme le jeu est équilibré il n'a pas d'influence sur les inégalités. Ceci est bien sur faux au vu du paragraphe précédent mais on peut proposer un argument plus général. Une manière usuelle de mesurer les inégalités parmi \(n\) personnes est de construire un indicateur en utilisant une fonction convexe \(f\). \[ I(X)=\sum_{i=1}^{n}f(X_{i})\qquad X_{i}=\text{argent de la i-ème personne} \] Pour un exemple réellement en pratique : \[ \text{Coefficient de Gini =}\sum_{i,j}|X_{i}-X_{j}| \] On a l'affirmation suivante : Pour des jeux équilibré, par Jensen \(I(X)\) est une sous-martingale : en espérance elle augmente à chaque tirage aléatoire. La morale de la fable pourrait donc être la suivante : tous les jeux : casino, paris sportifs ou jeu en bourse s'il se disent «équilibrés» ont pour impact d'augmenter les inégalités.

Une simple matrice pour l'inflation

On considère un modèle extrèmement simple pour représenter l'économie. Le tout est un grand graphe orienté \(G=(S,A)\) où chaque «agent économique» est représenté par un sommet, deux sommets sont connectés si il y a un «échange commerciale» entre les deux et l'orientation indique qui est «client» ou «fournisseur».

À cela on ajoute une matrice de réponse \(R\in\mathbb{R}^{S\times S}\) qui décrit le comportement de chaque agent lorsqu'il est subit à une hausse de prix. La règle est simple : si l'agent \(i\in S\) voit ses frais augmenter de \(h_{i}\in\mathbb{R}\), il les répercute proportionnellement sur chacun de ses clients \(j\) en augmentant ses prix de \(R_{ij}h_{i}\). On peut regarder ce que donne ce modèle dynamiquement avec un temps discret. On part d'une situation à l'équilibre et la perturbe avec une augmentation. À chaque temps, les agents mettent à jour leurs prix et créent une nouvelle augmentation. \[ H^{(0)}\in\mathbb{R}^{S}\qquad H^{(n+1)}=RH^{(n)}. \] En cumulée, l'augmentation total par rapport à la situation initiale est alors \[ C^{(n)}=(I+R+R^{2}+\cdots+R^{n})H^{(0)}\underset{n\rightarrow\infty}{\rightarrow}(I-R)^{-1}H^{(0)} \] ce qui donne une formule très simple la réponse au temps long si le rayon spectral de \(R\) est inférieur à \(1\). Un cas particulier naturel est justement de supposé \(R\) une matrice stochastique : \(\sum_{j}R_{ij}=1\) pour tout \(i\in S\) qui correspond pour les agents répercutent l'augmentation complètement sur leur clients. Dans ce cas au temps long \[ C^{(n)}\sim n\sum_{i\in S}H_{i}^{(0)}\times u^{R} \] où \(u^{R}\) est le vecteur propre de \(R\) associé à la valeur propre égale à \(1\). Ici les prix augmentent de manière continue et régulière. Un dernier cas est si \(R\) admet une valeur propre \(\lambda>1\) (si les agents anticipent la hausse des prix par exemple) on a alors une inflation qui explose de manière exponentielle. Pour finir on peut introduire une matrice diagonale \(D=\text{diag}((1-\sum_{j}R_{ij})_{i})\) qui décrit la proportion de la hausse que l'agent subit effectivement au temps long on a \[ D(I-R)^{-1}H^{(0)}. \] Le problème de l'inflation tient alors un peu du dilemme du prisonnier : ce sont ceux qui contribuent le moins à l'inflation (\(D_{i}\) grand) qui en subissent le plus les conséquences.

Le message de ce post est le suivant : Pour un electron, la Théorie de De Broglie-Bohm est simplement un choix particulier de Jauge pour le groupe d'invariance \(U(1)\) et dans ce cas l'onde pilote s'identifie avec le potentiel vecteur de l'electromagnétisme.

Le groupe de Jauge \(U(1)\)

Écrivons l'équation de Schrodinger pour un electron avec le terme électromagnétique (avec \(e=\bar{h}=m=1\)). \[ i\partial_{t}\psi=\frac{1}{2}(i\nabla-A)^{2}\psi+V\psi \] Cette équation est invariante par l'action du groupe de Jauge \(U(1)\). C'est à dire qu' avec le changement suivant \[ \begin{cases} \hat{\psi}:=\psi e^{-if}\\ \hat{A}:=A-\nabla f\\ \hat{V}:=V+\partial_{t}f \end{cases}\quad f:\mathbb{R}^{4}\rightarrow\mathbb{R} \] on retrouve l'équation de Schrodingeur initiale \[ i\partial_{t}\hat{\psi}=\frac{1}{2}(i\nabla-\hat{A})^{2}\hat{\psi}+\hat{V}\hat{\psi}. \]

La mécanique Bohmienne

Pour obtenir la mécanique Bohmienne il suffit d'imposer la condition que \(\hat{\psi}\) est réelle. Sous cette condition on a \[ \partial_{t}\hat{\psi}=\Re(\partial_{t}\hat{\psi})=\Im(\frac{1}{2}(i\nabla-\hat{A})^{2}\hat{\psi}+\hat{V}\hat{\psi})=-\frac{1}{2}\hat{\psi}(\nabla.\hat{A})-(\hat{A},\nabla\hat{\psi}) \] et on obtient une équation de continuité pour la densité de courant \[ \begin{align*} \partial_{t}|\hat{\psi}|^{2} & =-|\hat{\psi}|^{2}(\nabla\cdot\hat{A})-2(\hat{A}\cdot\nabla\hat{\psi})\hat{\psi}=-\text{div}[|\hat{\psi}|^{2}\hat{A}] \end{align*} \] Ici la densité de probabilité s'écoule le long des ligne du potentiel vecteur \(\hat{A}\). Celui ci cependant n'est pas fixe mais évolue avec le choix de Jauge. Cette image assez jolie : Par exemple pour une particule chargée dans un champs magnétique puisque celle ci suit le vecteur potentiel et que \(B=\text{rot}(\hat{A})\), la particule tourne autour de l'axe du champs magnétique. Autre exemple, pour l'expérience de Aharonov Bohm cela accentue encore la perspective : Le vecteur potentiel décrit la dynamique de la particule mais est bien sur également sensible au champs magnétique au centre de l'expérience.

Annexes : Invariance de Jauge \(U(1)\)potentiel

En effet puisque \[ (i\nabla-\hat{A})\hat{\psi}=\psi e^{-if}\nabla f+ie^{-if}\nabla\psi-A\psi e^{-if}+\psi e^{-if}\nabla f=e^{-if}(i\nabla\psi-A\psi) \] on a \[ \begin{align*} (i\nabla-\hat{A})^{2}\hat{\psi} & =(i\nabla-\hat{A})\cdot e^{-if}(i\nabla\psi-A\psi)\\ & =e^{-if}(i\nabla-A)\cdot(i\nabla\psi-A\psi)\\ & =e^{-if}(i\nabla-A)^{2}\psi \end{align*} \] et donc \[ \begin{align} i\partial_{t}\hat{\psi} & =(\partial_{t}f)\psi e^{-if}+e^{-if}(i\partial_{t}\psi)\label{eq:DeriveTemps}\\ & =(\partial_{t}f)\psi e^{-if}+e^{-if}(\frac{1}{2}(i\nabla-A)^{2}\psi+V\psi)\nonumber \\ & =\frac{1}{2}(i\nabla-\hat{A})^{2}\hat{\psi}+\hat{V}\hat{\psi}\nonumber \end{align} \]

Annexes : Evolution du choix de Jauge

\[ 0=\Re(i\partial_{t}\hat{\psi})=-\frac{1}{2}\Delta\hat{\psi}+(\frac{1}{2}\hat{A}^{2}+V+\partial_{t}f)\hat{\psi} \] et donc \[ -\partial_{t}f=\frac{1}{2}\hat{A}^{2}+V+\frac{\Delta\hat{\psi}}{2\hat{\psi}}. \] On observe ici \(\frac{\Delta\hat{\psi}}{2\hat{\psi}}\) appelé le ``potentiel quantique de la mécanique Bohmienne''.

Tous les élèves de lycée connaissent le théorème fondammental de l'arithmétique à savoir que l'on peut décomposer tout entier \(n\) en produit de puissance de nombre premiers \[ n=\prod_{p\in{\cal P}}p^{v_{p}(n)}\quad\text{avec}\,v_{p}\text{ la valuation }p\text{-adique.} \] Ce que les lycéens n'apprennent pas par contre c'est ``Comment choisir un entier aléatoirement ?'' Il est vrai qu'à première vue cette question semble ne pas avoir de sens. D'un côté on peut arbitrairement construire une infinité de mesure de probabilité mais par contre il n'existe pas de ``loi uniforme'' sur tous les entiers. Le message de ce post est que malgré tout, si on veut faire de l'arithmétique, une certaine famille de lois aléatoires est un peu préférables aux autres.

LES ``LOIS ZETA''

La loi considérée est la suivante \[ \mathbb{P}(X=n)=\frac{1}{\zeta(\beta)n^{\beta}}\quad\text{avec}\quad\zeta(\beta)=\sum_{n\geq1}\frac{1}{n^{\beta}}\quad\beta>1 \] où la fonction zeta de Riemann apparait ici de tel sorte que la somme des probabilités soit bien égale à 1. Sa propriété la plus remarquable est la suivante : sous cette loi ci \[ (V_{p}:=v_{p}(X))_{p\in{\cal P}}\text{ sont indépendantes et de loi }:\mathbb{P}(V_{p}=k)=(1-p^{-\beta})p^{-\beta k} \] Il est possible de vérifier cette propriété directement par calcul mais je vais plutôt présenter une analogie intéressante avec la physique statistique. Sur les entiers on introduit le Hamiltonien définit par \[ H(n):=\log n=\sum_{p\in{\cal P}}v_{p}(n)\log p\qquad\mathbb{P}(X=n)\sim e^{-\beta H(n)}. \] et on considère la probabilité tel que(ensemble canonique). Cela redonne bien la loi précédente. On peut remarquer ici que \(H\) a la forme d'une simple somme dans la décomposition \((v_{p}(n))_{p\in{\cal P}}\in\Omega=\mathbb{N}^{{\cal P}}\). En physique on dirait qu'il n'y a pas d'interactions et donc que les sous système \((v_{p}(n))_{p\in{\cal P}}\) sont indépendants. (preuve : on a la factorisation de la loi \[ \mathbb{P}(X=n)\sim\prod_{p\in{\cal P}}p^{-\beta v_{p}(n)} \] et donc l'indépendance.) On peut calculer la fonction de partition du sous système associé au facteur premier \(p\) : \(v_{p}(n)\in\mathbb{N}\) et d'{}''énergie'' \(v_{p}(n)\log p\) \[ Z_{p}(\beta):=\sum_{k=0}^{\infty}e^{-\beta k\log p}=\sum_{k=0}^{\infty}p^{-\beta k}=\frac{1}{1-p^{-\beta}}. \] Puisque les systèmes sont indépendants la fonction de partition du système total est simplement le produit des fonctions de partition des sous systèmes. On retrouve ici la forme du produit Eulérien pour la fonction zeta \[ Z(\beta):=\sum_{n\geq1}e^{-\beta H(n)}=\sum_{n\geq1}\frac{1}{n^{\beta}}=\zeta(\beta)=\prod_{p\in{\cal P}}Z_{p}(\beta)=\prod_{p\in{\cal P}}\frac{1}{1-p^{-\beta}} \]

Diviseur et PGCD

Une autre propriété remarquable est que pour la divisibilité, on a simplement \[ \mathbb{P}(d\text{ divise }X)=\frac{1}{d^{\beta}}. \] On peut également s'intéresser au pgcd de deux telles variables aléatoires indépendantes \(X\) et \(Y\) de parametre \(\beta\) et \(\gamma\). Dans ce cas, le pgcd est alors aussi une ``loi zeta'' de paramètre \(\beta+\gamma\). \[ \mathbb{P}(X=n)=\frac{1}{\zeta(\beta)n^{\beta}}\text{ et }\mathbb{P}(Y=n)=\frac{1}{\zeta(\gamma)n^{\gamma}}\Rightarrow\mathbb{P}(\text{pgcd}(X,Y)=n)=\frac{1}{\zeta(\beta+\gamma)n^{\beta+\gamma}} \] preuve : Chaque valeurs p-adiques restent indépendante et on a \[ \mathbb{P}(v_{p}(\text{pgcd}(X,Y))\geq k)=\mathbb{P}(v_{p}(X)\geq k)\mathbb{P}(v_{p}(Y)\geq k)=p^{-k(\beta+\gamma)}. \] Une dernière motivation que l'on peut mentionner est la limite lorsque \(\beta\rightarrow1\). L'heuristique est qu'elle devrait d'une certaine manière converger vers la ``loi uniforme sur tous les entiers''. Plus précisément, on aimerait pouvoir affirmer qu'on obtient les mêmes assymptotiques que d'autres lois qui "convergent vers la loi uniforme", par exemple \(\{1,2,\cdots,N\}\) lorsque \(N\rightarrow\infty\), . Typiquement \[ \mathbb{P}(d\text{ divise }X)\rightarrow\frac{1}{d} \]

Fonction multiplicative

Comme autre exemple d'application de l'indépendance des \(V_{p}\) pour les lois zeta, voici quelques formules assez surprenant lorsqu'on les voit pour la première fois. \[ \sum_{n\geq1}\frac{\mu(n)}{n^{\beta}}=\frac{1}{\zeta(\beta)}\qquad\sum_{n\geq1}\frac{\phi(n)}{n^{\beta}}=\frac{\zeta(\beta-1)}{\zeta(\beta)} \] où \(\phi\) et \(\mu\) sont les fonctions indicatrice d'Euler et de Mobus. En arithmétique on appelle ``fonction multiplicative'' les fonction qui satisfont \(f(pq)=f(p)f(q)\) pour tout \(p,q\) premiers entre eux. Avec la décomposition en facteurs premiers on a directement \[ f(n)=\prod_{p\in{\cal P}}f(p^{v_{p}(n)})=\prod_{p\in{\cal P}}f_{p}(v_{p}(n))\quad\text{où }f_{p}(k):=f(p^{k}). \] Avec une loi zéta et par indépendance on a alors \[ \mathbb{E}_{\beta}[f(X)]=\mathbb{E}_{\beta}[\prod_{p\in{\cal P}}f_{p}(v_{p}(X))]=\prod_{p\in{\cal P}}\mathbb{E}_{\beta}[f_{p}(v_{p}(X))] \] Pour la fonction de Mobius : \[ \mu(n):=\begin{cases} 0 & \text{si divisible par un carré}\\ 1 & \text{si produit d'un nombre pair de premier}\\ -1 & \text{si produit d'un nombre impair de premier} \end{cases} \] \[ \mu_{p}(k)=\begin{cases} 1 & \text{si }k=0\\ -1 & \text{si }k=1\\ 0 & \text{sinon} \end{cases}\quad\Rightarrow\quad\mathbb{E}_{\beta}\mu_{p}(v_{p}(X))=(1-p^{-\beta})^{2} \] et donc \[ \frac{1}{\zeta(\beta)}\sum_{n\geq1}\frac{\mu(n)}{n^{\beta}}=\mathbb{E}_{\beta}[\mu]=\prod_{p\in{\cal P}}(1-p^{-\beta})^{2}=\frac{1}{\zeta(\beta)^{2}} \] Avec la fonction indicatrice d'Euler \[ \overline{\phi}(n):=\frac{\phi(n)}{n}=\frac{1}{n}\#\{m\leq n:\text{pgcd}(m,n)=1\} \] \[ \overline{\phi}_{p}(k)=\begin{cases} 1 & \text{si }k=0\\ 1-p^{-1} & \text{si }k\geq1 \end{cases}\quad\Rightarrow\quad\mathbb{E}_{\beta}[\overline{\phi}_{p}]=1-p^{-1-\beta} \] et donc \[ \frac{1}{\zeta(\beta)}\sum_{n\geq1}\frac{\phi(n)}{n^{\beta+1}}=\mathbb{E}_{\beta}[\overline{\phi}]=\prod_{p\in{\cal P}}(1-p^{-(\beta+1)})=\frac{1}{\zeta(\beta+1)} \] Convolution de Dirichlet comme somme de variables indépendantes \[ \mathbb{E}(z^{-\beta})=\mathbb{E}(x^{-\beta})\mathbb{E}(y^{-\beta}) \] Soit deux variables aléatoires indépendantes à valeur sur \(\Omega=\mathbb{N}^{{\cal P}}\). On peut considérer leur somme ce qui implique une ``convolution'' l'espace \(\Omega\) (de dimension infini) \[ \mathbb{P}(\boldsymbol{Z}:=\boldsymbol{X}+\boldsymbol{Y}=\boldsymbol{k})=\sum_{\boldsymbol{k}_{1}+\boldsymbol{k}_{2}=\boldsymbol{k}}\mathbb{P}(\boldsymbol{X}=\boldsymbol{k}_{1})\mathbb{P}(\boldsymbol{Y}=\boldsymbol{k}_{2})\quad\boldsymbol{k}\in\mathbb{N}^{{\cal P}} \] Puisque \(\boldsymbol{X}\) et \(\boldsymbol{Y}\) sont indépendant on a \[ \mathbb{E}e^{t.\boldsymbol{Z}}=\mathbb{E}e^{t.\boldsymbol{X}}\mathbb{E}e^{t.\boldsymbol{Y}}\quad\forall t\in\mathbb{C}^{{\cal P}} \] On écrit \(x\) (resp \(y\) et \(z\)) l'entier tel que \(\boldsymbol{X}=(v_{p}(x))_{p\in{\cal P}}\) (resp \(\boldsymbol{Y},\boldsymbol{Z}\)). Puisque \[ \forall p\in{\cal P}\,v_{p}(z)=v_{p}(x)+v_{p}(y)\Leftrightarrow z=xy \] on a alors \[ \mathbb{P}(z=n)=\sum_{d_{1}\times d_{2}=n}\mathbb{P}(x=d_{1})\mathbb{P}(y=d_{2})\quad n\in\mathbb{N}^{\mathbb{N}} \] Ceci est la convolution de Dirichlet que l'on pourra noté \(\mathbb{P}_{z}=\mathbb{P}_{x}\star\mathbb{P}_{y}\). Un cas particulier de \(t:=(\beta\log p)_{p\in{\cal P}}\in\mathbb{C}^{{\cal P}}\) \[ \mathbb{E}e^{t.\boldsymbol{Z}}=\sum_{n\geq1}\mathbb{P}(z=n)e^{\beta\sum_{p\in{\cal P}}v_{p}(n)\log p}=\sum_{n\geq1}\frac{\mathbb{P}(z=n)}{n^{\beta}} \] ''Transformé de Fourier'' sur les entiers. Cette transformé se comporte correctement vis à vis de la convolution de Dirichlet de la mème manière que la transformé de Fourier vis à vis de la convolution dans \(\mathbb{R}^{n}\). \[ \sum_{n\geq1}\frac{\mathbb{P}(z=n)}{n^{\beta}}=\left(\sum_{n\geq1}\frac{\mathbb{P}(x=n)}{n^{\beta}}\right)\left(\sum_{n\geq1}\frac{\mathbb{P}(y=n)}{n^{\beta}}\right) \] Plus généralement \[ h=f\star g\quad\Rightarrow\quad\sum_{n\geq1}\frac{h(n)}{n^{\beta}}=\left(\sum_{n\geq1}\frac{f(n)}{n^{\beta}}\right)\left(\sum_{n\geq1}\frac{g(n)}{n^{\beta}}\right) \] Je termine ce post par une remarque : Tout ce que a été fait ici utilise la décomposition en nombre premier mais pas leur valeur particulières. On ne donc pas utiliser ces outils pour estimer la répartition des nombres premiers... à moins d'avoir d'autres moyen d'estimer la fonction \(\zeta\) !

Introduction

On a tous vu de nombreuse fois ces images pour illustrer les principes de relativité générale : la terre déforme l'espace-temps autour d'elle de la même manière qu'une boule de pétanque posée sur un drap élastique. L'analogie continue en ajoutant une petite bille dont la trajectoire est déviée, suivant la déformation du drap, lorsqu'elle passe à coté de la terre. C'est la gravitation. Le but de ce poste est de proposer une autre image pour illustrer la théorie d'Einstein, un peu moins parlante mais plus fidèle d'un point de vue mathématique. De fait il est très difficile de dessiner la relativité générale. Il s'agit d'un espace courbé à 4 dimensions et l'équation possède \(10\) variables libres. Tout cela sera donc simplifier au maximum On écrit l'équation d'Einstein

\[ \boxed{R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R=T_{\mu\nu}} \]

Une toupie en dimension 1+1

Ici je me restreint à une dimension d'espace et à une dimension de temps (d=1+1). En dimension \(2\),il n'y a qu'un paramêtre libre pour \(R_{\mu\nu}\) à savoir la \(K\) la courbure de Gauss et pour coller avec les équations d'Einstein on supposera que celle ci est proportionnelle à la densité de masse

\[ K=\rho. \]

Quel est alors l'influence d'une masse immobile dans l'espace que l'on nommera ``terre''? Puisque l'on considère la dimension du temps, la terre n'est pas un point mais une droite en fixant le centre à 0 elle est décrite par \(\mathcal{T}=\{(0,t),t\in\mathbb{R}\}\). La courbure est alors égale à m sur cette droite et nulle ailleur. Paradoxalement le reste de l'espace est ``plat'' c'est à dire de courbure nulle. Si on cherche maintenant en géométrie une surface qui correspond on peux proposer une toupie formé de deux cones identiques collé bout à bout.

En effet sur cette toupie la courbure vaux \[ K=\begin{cases} \frac{2\alpha}{R} & \text{sur la couronne}\\ 0 & \text{sur les surface}\\ "\infty" & \text{aux pointes} \end{cases} \] avec \(R\) le rayon du grand cercle au centre et \(\alpha\) l'angle que forme les deux parties du cone au niveau de la couronne. Remarquer que la courbure sur chaque cone est bien nulle comme on peut l'aplatir sur une table. En oubliant les pointes on a ici une solution à notre équation d'Einstein 2D en faisant correspondre \(m\sim\frac{2\alpha}{R}\). Pour un \(m\) grand Pour \(m\rightarrow0\) correspond à \(\alpha\rightarrow0\) c'est à dire une toupie très allongée jusqu'à la limite m=0 vers un cylindre (donc une surface complètement plane).

Un exemple de dynamique

Maintenant que nous avons la géométrie (alias le champs de gravitation) nous pouvons nous interesser à la dynamique. Regardons donc l'évolution d'une petite bille lachée librement dans ce système. Il s'agit ici de tracer une géodésique sur la toupie. Pour cela il suffit de déplier le patron de la figure, la géodésique est alors une simple ligne droite. Ci dessous la trajectoire de la bille partant de la terre puis retombant dessus.

En notant \((r,\theta)\) la position sur le cone et \(R_{*}=\frac{R}{\sin\alpha}\) le rayon du cone On obtient avec un peu de trigonométrie. \[ \begin{align*} \text{temps }t & =R_{*}\theta\\ \text{position }x & =R_{*}-r\\ \text{vitesse initiale }v_{0} & =\tan\beta\\ \text{trajectoire }x(t) & =R_{*}\left(1-\frac{\cos\beta}{\cos(R_{*}^{-1}t+\beta)}\right) \end{align*} \] Si ce résultat n'est pas forcement très parlant on peut supposer \(R_{*}^{-1}t\) et \(\beta\) petits, faire un développement limité et le comparer avec le cas classique (accélération = g =constante). \[ x^{\text{relativité}}(t)\approx\tan\beta.t-\frac{1}{2R_{*}}t^{2},\qquad x^{\text{classique}}(t)=v_{0}t-\frac{g}{2}t^{2} \] et on peut donc bien identifier \[ g=\frac{1}{R_{*}}=\frac{\sin\alpha}{R}\sim\frac{\sin mR}{R}\sim m \]

Je presente ici une idée très jolie signée Adi Shamir (le "S" dans "RSA"). Celle ci a déjà fait l'objet d'un article sur le site d'Images des Maths et comme elle est superbe je me permet de la réexpliqué ici. Un groupe de personnes partage un coffre fort (avec codes à chiffre) et décide d'organiser ensemble la sécurité. Le premier membre propose de simplement donner le code à chacun. Mais le reste du groupe n'est pas d'accord car la sécurité ne serait alors pas très élevée. Il suffit d'un membre soit malhonnête pour que tout soit compromis. Le deuxième membre propose de diviser la clef de sécurité en morceau et d'en donner un à chacun à la même manière des pirates découpant une carte au trésor. La seule façon d'ouvrir le coffre est alors que le groupe tout entier se réunisse. Mais cette idée est également rejetée car contre trop contraignante. Si un membre n'est plus là ou si il a oublié son code, le contenu du coffre est perdu. Un troisième membre ne propose rien mais fait alors remarquer que plusieurs personnes du groupe (mais on ignore lesquelles mais moins que (k-1)) se mettraient volontier ensemble pour partager leurs informations et ouvrir le coffre au détriment du reste du groupe. Le groupe se met alors d'accord sur le cahier des charges suivant: "Si au moins k membres du groupe se réunissent ils doivent toujours être capables d'ouvrir le coffre mais si il n'y a seulement que (k-1) personnes, alors il doit leur être impossible de deviner la combinaison." La difficulté ici est qu'il faut ces conditions doivent être valides quelsque soient les sous ensembles de k ou (k-1) personnes. Une solution très élégante utilise de l'algèbre linéaire et je la présente maintenant. Soit une famille de n vecteurs de dimension k : (a1,...,an) telle que pour toute sous famille de k vecteurs forme une base. Le code consiste maintenant en un vecteur c de de dimension k. A la i-ème personnes du groupe on donne comme information le vecteur ai et le réel bi = (ai,c). Pourquoi cela fonctionne ? Avec la propriété des (ai) pour tout sous ensemble L on a un système d'équation à |L| élément dont l'ensemble des solutions est un espace affine de dimension k-|L| et qui admet donc une infinité de solution pour \(|L\leq k\). Par contre avec k personnes il suffit de résoudre un système à k équations et k inconnus (avec un pivot de Gauss). Voici un exemple avec goupe de n=5 personnes (A,B,C,D et E) et k=3.

\[ \begin{cases} A & c_{1}+3c_{2}-c_{3}=-2\\ B & 3c_{1}+c_{3}=11\\ C & 4c_{1}+c_{2}+c_{3}=13\\ D & 2c_{2}+3c_{3}=4\\ E & c_{1}-c_{2}+7c_{3}=18 \end{cases} \]

Si par exemple B,C et E se réunissent. Ensemble ils obtiennent le système suivant qu'ils peuvent facilement résoudre.

\[ \begin{cases} B & 3c_{1}+c_{3}=11\\ C & 4c_{1}+c_{2}+c_{3}=13\\ E & c_{1}-c_{2}+7c_{3}=18 \end{cases}\Rightarrow\begin{cases} c_{1}=3\\ c_{2}=-1\\ c_{3}=2 \end{cases} \]

Mais bien sur avec seulement les équations de \(B\) et \(C\) ou seulement celles de \(C\) et \(E\), on obtient une infinité de solution. Il reste la question de comment construire une telle famille de vecteurs ai? Une première méthode un peu bête mais très efficace et de simplement tirer des vecteurs aux hasards. Puisque det = 0 est une sous variété de dimension inférieur la probabilité de toucher cet espace est nulle avec une probabilité continue. Une deuxième méthode (et celle proposée initialement) et de se placer dans l'espace des polynomes de degré k-1. Le code consiste en les coefficients d'un polynome P et on donne comme information à chacun (x,P(x)) pour des valeurs x différents. Si on revient à notre exemple à 5 personnes, on pourrait avoir

\[ \begin{cases} A & P(1)=c_{1}+c_{2}+c_{3}=4\\ B & P(2)=c_{1}+2c_{2}+4c_{3}=9\\ C & P(3)=c_{1}+3c_{2}+9c_{3}=18\\ D & P(4)=c_{1}+4c_{2}+16c_{3}=31\\ E & P(4)=c_{1}+5c_{2}+25c_{3}=48 \end{cases} \]

Ceci satisfait les conditions du problème car le déterminant de Vandermond est non nul dès que les x sont différents. Ici résoudre le système est également facile en utilisant les polynomes d'interpolation de Lagrange.

L'un des plus beau résultat en géométrie différentiel est le théorème de Gauss Bonnet. Pour toute surface \(S\) fermée et plongée dans \(\mathbb{R}^{3}\), l'intégrale de sa \og courbure\fg{} \(K\) est égale à sa caractéristique d'Euler \(\chi(S)\) \[ 2\pi\chi(S)=\iint K(u)du \] Mentionnons également le théorème que Gauss appelait lui même \og théorème remarque\fg : si on peut transformé une surface \(S\) en une surface \(S'\) par une \og isométrie\fg{} \(\phi\) alors la courbure au point \(\phi(u)\) dans \(S'\) égale à la courbure du point \(u\) dans \(S\). Ici nous présentons une version un peu simplifiée du théorème de Gauss Bonnet mais dont la preuve est élémentaire. Elle peut être présenté à des collégiens et donc constitue un sujet parfait pour un exposé de vulgarisation. Tout d'abord considérons une figure dans le plan. Et rappelons que pour un polygone à \(N\) cotés la somme des angles vaut \((N-2)\pi\). En effet faisons le tour de ce polygone dans le sens des aiguilles d'une montre en notant à chaque fois l'angle sur lequel on a tourné. On comptera ce tournant positivement si il est vers la droite et négativement si il est vers la gauche.

Après un tour complet la somme des tournants vaut \(\sum_{i}\theta_{i}=2\pi\) ceci quelque soit le nombre de tournant réalisés. Sur chaque sommet du polygone la somme du tournant \(\theta_{i}\) et de l'angle au sommet \(\alpha_{i}\) vaut toujours \(\theta_{i}+\alpha_{i}=\pi\). Et donc \(\sum_{i=1}^{N}\alpha_{i}=N\pi-\sum\theta_{i}=N\pi-2\pi\). Attaquons maintenant nous aux solides en 3d. Nous avons un polyèdre. Peut-on définir sur ses sommets une notion de \og coin\fg ? Quelque chose d'équivalent au angles en 2D et qui mesure de combien le sommet est pointu? On défini le coin d'un sommet de la manière suivante : Au sommet \(A\), plusieurs faces du polyèdre se rejoignent, chacune ayant un angle \(\alpha_{i}\) en ce sommet. On défini alors le coin \(c_{A}\) comme \(2\pi\) moins la somme de ces angles \(\alpha\). \[ c_{A}=2\pi-\sum_{i\sim A}\alpha_{i} \] Exemple : pour un cube :

Les trois angles ici valent \(\frac{\pi}{2}\) et donc \(c_{A}=2\pi-3\times\frac{\pi}{2}=\frac{\pi}{2}\). Deuxième exemple pour un tétraèdre régulier :

Ici les trois angles valent \(\frac{\pi}{3}\), et donc \(c_{A}=2\pi-3\times\frac{\pi}{3}=\pi\]. Remarquez qu'il peut y avoir des coins négatifs. Cependant ce ne dépend pas si le coin est s'enfonce ou non dans la figure. Par exemple le coin ci dessous est bien positif

Il est facile de voir si un coin est positif ou négatif en dépliant le patron de la figure. Si sur le patron les faces autour du sommet ne se recouvrent pas alors \(\sum\alpha_{i}\leq2\pi\) et au contraire si elles se recouvrent alors \(\sum\alpha_{i}>2\pi\). Intéressons nous maintenant à la somme des coins du solide. Reprenons les exemples précédents: pour le cube, on a \(8\) sommets, chacun d'un coin égale à \(\frac{\pi}{2}\), la somme des coins vaut alors \(\sum_{s\text{ du cube}}c_{s}=8\times\frac{\pi}{2}=4\pi\) . Pour le tétraèdre, on a \(4\) sommets dont chacun a un coin égale à \(\pi\) et donc la somme vaut \(\sum_{s\text{ du tétraèdre}}c_{s}=4\times\pi=4\pi.\) On retrouve à chaque fois la surface d'une sphère qui vaut également \(2\pi\chi(S)\). Pour un polyèdre \(\mathcal{P}\), montrons la relation \(\sum_{s\text{ du polyèdre}}c_{s}=2\pi\chi(\mathcal{P})\). \begin{align*} \sum_{s}c_{s} & =\sum_{s}(2\pi-\sum_{i\sim s}\alpha_{i})\\ & =2\pi S-\sum_{s}\sum_{i\sim s}\alpha_{i} \end{align*} avec \(S\) le nombre de sommets. Le deuxième terme \(\sum_{s}\sum_{i\sim s}\alpha_{i}\) est la somme de tous les angles du polyèdre, c'est donc aussi la somme sur toutes les faces \(f\) de la somme des angles de cette face: \[ \begin{align*} \sum_{s}c_{s} & =2\pi S-\sum_{f}\sum_{i\in f}\alpha_{i}\\ & =2\pi S-\sum_{f}(N_{f}\pi-2\pi) \end{align*} \] avec \(N_{f}\) le nombre de coté de la face \(f\). Dans la somme \(\sum_{f}N_{f}\) chaque arête du polyèdre est compter 2 fois, on a donc alors \(\sum_{f}N_{f}=2A\) avec \(A\) le nombre d'arête du polyèdre. On a donc bien \[ \sum_{s}c_{s}=2\pi(S-A+F)=2\pi\chi(\mathcal{P}) \] On peut énoncé le théorème suivant : la somme des coins d'un solide (sans trou) vaut toujours \(4\pi\). Remarque élémentaire Considérons le cas où un polyèdre \(\mathcal{P}\) ne possède que des faces triangulaires (il est toujours possible se ramener à ce cas ci en ajoutant des arêtes). Et considérons une transformation dans l'espace \(\phi\), qui déforme \(\mathcal{P}\) en un autre polyèdre \(\phi(\mathcal{P})\) mais qui ne change pas la longueur des arêtes: pour toutes les arêtes \([A,B]\) de \(\mathcal{P}\), sa longueur est égale à la longueur de l'arête \([\phi(A),\phi(B)]\) de \(\phi(\mathcal{P})\). Pour chaque triangle de \(ABC\) qui forment les faces de \(\mathcal{P},\) le triangle \(\phi(ABC)\) a les même longueurs. On en déduit que les angles du triangle \(\phi(ABC)\) sont égaux à ceux de \(ABC\). En conclusion les coins \(c_{\phi(A)}=2\pi-\sum_{i\sim\phi(A)}\alpha_{i}=2\pi-\sum_{i\sim A}\alpha_{i}=c_{A}\) ne changent pas. Nous avons donc là un petit \og théorème remarquable\fg{} : Pour des triangulations, les coins sont donc invariant par isométrie.

La propriété la plus remarquable de la dérivée extérieur est sans aucun doute le théorème de Stokes : \[ \int_{\partial A}\omega=\int_{A}d\omega \] ''l'intégrale de la forme différentielle sur le bord de la sous variété est égale à l'intégrale de sa dérivée extérieur sur l'intérieur de cette sous variété''. Selon moi cela devrait même être la définition de la dérivée extérieur car elle donne immédiatenent l'intuition et la motivation de cette notion. Par exemple pour la notion ``vitesse'' la définition intuitive est ``la quantité qui intégré sur le temps donne la distance parcouru'' et de même, je pense que la définition intuitive de la dérivé exterieure \(d\omega\) devrait être ``la forme différentielle de degré supérieur qui satisfait le théorème de Stokes''. Avec cette définition, il est clair que la dérivée extérieure est une notion naturelle et centrale en analyse. Pourtant que ce soit en physique, en géoscience, en analyse numérique et dans pleins d'autres domaines on manipule constamment des champs de vecteurs sur des variétés mais souvent en ne les traitant que comme un ensemble de fonctions réelles sans se poser vraiment la question de la nature mathématique et ignorant au passages des très belles notions de géométrie différentielle ou topologie algébrique. Le but de ce poste est de donner deux exemples simples illustrant pourquoi l'algèbre différentielle et la dérivée extérieur (et la cohomologie de De Rham) sont naturelles et devraientt être utilisées plus souvent. Soit M une variété de dimension \(n\). L'algèbre des formes différentielles \(\Lambda(M)\) est une algèbre graduée où la dérivée extérieur d va des k-formes differentielles au (k+1)-formes différentielles \[ \Lambda^{0}(M)\xrightarrow{d}\Lambda^{1}(M)\xrightarrow{d}\cdots\xrightarrow{d}\Lambda^{n}(M) \] Ces espaces pouvant aussi être vu comme un champs de vecteurs de dimension k parmi n. La propriété algébrique principale est sans aucun doute \(d\circ d=0\): Pour tout espace des \(k\)-formes, l'image de \(d\) est incluse dans le noyau de \(d\). Tout le jeu de la cohomologie de De Rham est de comprendre quand a t-on l'égalité entre l'image et le noyau et plus généralement quel est l'espace ``manquant''.

La cohomologie de \(\mathbb{R}^{3}\).

Dans le cas d'une variété de dimension \(3\) par exemple \(\mathbb{R}^{3}\), la différentielle extérieur est bien connu mais sous des noms différents de gradient, divergence ou rotationel \[ \Lambda^{0}(\mathbb{R}^{3})\xrightarrow{\text{grad}}\Lambda^{1}(\mathbb{R}^{3})\xrightarrow{\text{rot}}\Lambda^{2}(\mathbb{R}^{3})\xrightarrow{\text{div}}\Lambda^{3}(\mathbb{R}^{3}). \] Remarque: les dimension de \(\Lambda^{k}(\mathbb{R}^{3})\) sont respectivement \)1,3,3\) et \(1\). Ici la propriété \(d\circ d=0\) n'est rien d'autre que les relations bien connus \(\text{rot}\circ\text{grad}=0\) et \(\text{div}\circ\text{rot}=0\). Ici la cohomologie de De Rham de \(\mathbb{R}^{3}\) c'est très facile car l'espace est homotope à un point: pour les 0-formes :\)\text{Ker}(d)/\text{Im}(d)=\mathbb{R}\), c'est à dire on a \(\text{grad}(f)=0\) ssi il existe \(c\) constante telle que \(f=c\), pour les 1-formes :\(\text{Ker}(d)/\text{Im}(d)=0\), c'est à dire \(\text{rot}(u)=0\) ssi il existe une fonction \(f\) telle que \(u=\text{grad}(f)\), pour les 2-formes :\(\text{Ker}(d)/\text{Im}(d)=0\), c'est à dire\(\text{div}(v)=0\) ssi il existe une 1-forme \(u\) telle que \(v=\text{rot}(u)\), pour les 3-formes \(\text{Ker}(d)/\text{Im}(d)=0\), il existe toujours une solution à \(\text{div}(v)=g\).

Les équations de Maxwell

Ici nous écrivons les équations de Maxwell dans le formalisme des formes différentielles. On rappelle que sur les formes différentielle on définit aussi la dualité \(*\) entre les \(k\) formes et les \(n-k\) formes (pour faire simple \[ *:\bigwedge_{i\in I}dx_{i}\leftrightarrow\bigwedge_{i\notin I}dx_{i} \] ). Ceci permet de définir \(\partial=*d*\) allant des \(k\) formes au \((k-1)\) formes. La théorie de Maxwell est donné par le magnifique schéma suivant

Remarquer que \(\Lambda^{1}(\mathbb{R}^{4})\) et \(\Lambda^{2}(\mathbb{R}^{4})\) sont de dimension \(4\) et \(6\). On a noté ici

• le \(4-\)vecteur \(A^{\mu}=(V,A)\) (le potentiel, et le potentiel vecteur),
• Le \(J^{\mu}=(\rho,j)\) (la densité de charge et de courant)
• Le \(6-\)vecteur \((E,B)\) le champs electromagnétique.

Le premier avantage ici est que tout est énoncé à un niveau ``géométrie'' sans un choix particulier de paramétrage. On n'a donc pas à se préocupper de changements de base (changement de référentielle pour un physicien, changement de carte pour un mathématicien). En particulier il est clair que les champs electriques et magnétiques sont indissociables. Le deuxième avantage est que les notion de k-forme ne sont pas arbitraire mais au contraire sont tout à fait naturel d'un point de vu physique: Une densité de charge s'intégre sur un volume (3-forme), le courant de charge s'intègre sur une surface fois un temps (3-forme), le champs magnétique s'intégre sur une surface (2-forme) et le potentiel vecteur s'intègre sur un chemin (1-forme). En mécanique quantique ce dernier est lié à la phase de la fonction d'onde de l'électron. Chaque flèche du diagramme n'est rien d'autre que la dérivée extérieur dont je donne ci dessous le sens physique:

• (1) C'est ici le choix de Jauge, on peut arbitrairement changer \[ V\rightarrow V-\frac{\partial f}{\partial t}\quad\text{et}\quad A\rightarrow A+\text{grad}(f) \] sans changer les champs électromagnétiques, en effet \((3)\circ(1)=0\).
• (2) Un choix particulier de Jauge est \((2)=0\) appeléé la Jauge de Lorentz: \[ \frac{\partial V}{\partial t}+\text{div}(A)=0. \] C'est la plus couramment utilisé en électromagnétisme.
• (3) On peut exprimer le champs electromagnétisme en fonction du potentiel vecteur : \[ E=-\frac{\partial A}{\partial t}-\text{grad}(V)\quad\text{et}\quad B=\text{rot}(A). \]
• (4) On a ici les équations de Maxwell-Faraday et Maxwell-Thomson \[ \frac{\partial B}{\partial t}+\text{rot}(E)=0\quad\text{et}\quad\text{div}(B)=0 \] qui découlent bien sur de \((4)\circ(3)=0\).
• (5)] C'est maintenant les équations de Maxwell-Gauss et Maxwell-Ampere \[ \text{div}(E)=\rho\quad\text{et}\quad-\frac{\partial E}{\partial t}+\text{rot}(B)=j \]
• (6)] C'est la loi de conservation de la charge \[ \frac{\partial\rho}{\partial t}+\text{div}(j)=0 \] qui est encore \((6)\circ(5)=0\).

J'en profite pour une petite remarque historique, en 1865 l'idée géniale de Maxwell fut de remarquer qu'avec l'équation d'Ampère dans la version où elle était énoncée à l'époque \((6)\circ(5)\) ne donnait pas \(0\). Il la modifia alors en ajoutant le terme \(\frac{\partial E}{\partial t}\) rendant ainsi la théorie cohérente. Ainsi ce fut donc bien des considérations de topologie algébrique qui menèrent à la théorie de l'électromagnétisme (classique) telle qu'on la connait aujourd'hui.

Un petit problème du collectionneur (généralisé)

Je souhaiterai apprendre une langue comme le chinois par exemple. Pour cela je procède de la façon suivante. J'ouvre un livre, la radio ou la Télé et au hasard, je choisis un mot que j'écrit sur un cahier et je l'append. Puis je recommence plusieurs fois. Si je tombe sur un mot que je connais déjà tant pis, je n'apprend rien de nouveau. Pour ce problème on introduit naturellement la loi de probabilité p(i) sur les mots i qui est la fréquence d'utilisation du mot en question dans la langue courante. Au bout de N (grand) itérations combien de mots ai je appris? Soit S une phrase avec quelle probabilité suis je capable de comprendre tous les mots S? Combien faut-il d'itération pour que je connaisse enfin tous les mots (Problème du collectionneur généralisé)?

Astuce utilisant la loi de Poisson

Il est possible d'obtenir très facilement une solution en modifions un peu le problème de la manière suivante : on remplace le nombre déterministe N d'itération par un nombre aléatoire tiré suivant une loi de Poisson de moyenne N. Ce changement ne modifie que très légèrement notre problème puisque l'on va tirer N caractères plus ou moins une erreur d'ordre racine de N (TCL). On utilise alors une propriété extrèmement utile de la loi de Poisson : ``Soit P une loi de poisson de paramètre d. Et X(1),X(2),X(3),... des variables aléatoire discrète sur un ensembre A et indépendante et identiquement distribué. Alors les variables \[ Y_{a}=\sum_{i=1}^{P}1_{X_{i}=a} \] pour a dans A forment une famille de variables aléatoires indépendente qui suivent une loi de Poisson de paramètre d fois Prob(X=a)'' On applique cette propriété à notre problème et on a que pour tout mot i, le nombre de fois que ce mot a été tiré est une loi de Poisson de paramètre Np(i). Je connais donc le mot avec proba 1-exp(-Np(i)). Qui plus est, le tirage de chaque mot est indépendant et donc par exemple je connaitrait la phrase ijk avec probabilité {[}1-exp(-Np(i){]}{[}1-exp(-Np(j)){]}{[}1-exp(-Np(k)){]} Et pour connaitre tous les mots avec proba \[ p=\prod_{i=1}^{|I|}(1-e^{-Np(i)}). \] Remarquer que pour p(i)=1/|I| (problème du collectionneur usuel), log(p) vaux environ -|I|exp(-N/|I|) et donc p vers 1 si N plus grand que |I|log(|I|) et vers 0 si N plus petit que |I|log(|I|). Pour un problème d'apprentissage élémentaire par ordinateur, ceci donne un idée grossière du nombre de données à utiliser.

Le modèle grand canonique en physique statistique

Le modèle grand canonique, universellement utilisé en physique statistique utilise plus ou moins la même astuce. Plutôt que d'étudier le système avec N particules (modèle canonique) on relache cette contrainte et on laisse le nombre de particules aléatoire dont la loi est centré autour de N. Par exemple : soit un système ayant k états d'énergie E(1),...,E(k) et N particules. L'énergie total E du système est la somme des E(i)N(i) avec N(i) le nombre de particule dans l'état i. La probabilité de chaque état est proportionnel à \(\sim e^{-\beta E}\) ce qui revient à dire que chaque particule se place en \(i\)avec proba \(p(i)=\frac{e^{-\beta E_{i}}}{\sum_{j}e^{^{-\beta E_{j}}}}\)de manière indépendant. Modifions le système en supposant que le nombre de particules est donné par une loi de Poisson de moyenne N. Alors le nombre de particules dans les états i, deviennent des loi de Poisson indépendantes et de paramètre Np(i) que l'on réécrit souvent introduisant le potentiel chimique \(e^{\beta\mu}:=\frac{N}{\sum_{j}e^{^{-\beta E_{j}}}}\) .

Un petit modèle de serveur

Voici un troisième petit modèle où cette astuce simplifie considérablement de problème. On dispose d'un arbre binaire de serveurs pour traiter des requêtes. Les requêtes arrivent à la racines. Si il n'y a qu'une requête, le serveur à la racine la traite. Si il y en a plus qu'une le serveur est saturé et ne fait rien. Par contre chaque requéte est redirigée vers l'un des deux serveur fils de l'arbre et de manière aléatoire (Bernoulli p=1/2 ) et indépendante. Les deux serveurs fils se comporte alors exactement de la mème manière, traitant une requète si elle est seule, ou redirigeant de manière aléatoire les requètes vers les serveurs suivant dans l'arbre.

Question : on envoie N requètes à la racine, quelle profondeur de l'arbre est nécessaire pour traiter ces requètes. Réponse : si on remplace le nombre de requète à la racine par une loi de poisson de paramètre N, alors après répartition le nombre de requètes de chaque serveur fils est donné par une loi de Poisson de paramètre N/2 et indépendante. On retrouve ainsi deux copies identique et indépendante de notre problème. À la profondeur k il y a 2 puissance k copies de Poisson de paramètre \(N/2^{k}\). La probabilité à ce qu'aucun serveur à cette profondeur n'ai deux requète est borné par \(2^{k}\big(1-\exp(-\frac{N}{2^{k}})(1+\frac{N}{2^{k}})\big)\approx2^{k}\cdot\frac{1}{2}(\frac{N}{2^{k}})^{2}\) si \(\frac{N}{2^{k}}\ll1\) . Soit \(2^{-k}N^{2}\approx1\)et donc \(k\approx2\log_{2}(N)\) .

Je présente ici deux petits modèles de théorie des jeux que je trouve intéressant car ils mènent à des conclusions complètement contraire à ce qu'on aurait pu s'attendre à première vu.

Une route trop efficace qui mène à des embouteillages.

Une ville A est connectée à une ville C par deux routes, celle passant par B et celle passant par D. Chacune est composée de deux tronçons : une partie route de campagne et une partie autoroute comme sur le schéma. Sur la route de campagne la vitesse est limité et le temps pour la parcourir est toujours le même \(1\) heure. Sur l'autoroute on peut aller plus vite mais si il y a trop de monde, on doit ralentir à cause des bouchons. Pour la traverser, on met p heure où\(p\)entre 0 et 1 est la proportion de personnes circulant sur la route. Les automobilistes cherchent toujours à mettre le moins de temps possible et choisiront une routes plus rapide si ils en ont l'occasion. Dans la situations présente si une proportion trop importante prennent la route, la deuxième devient plus rapide car moins fréquenté. Des automobilistes changeront alors de trajets les jours suivants. Les fréquentations s'équilibrent avec la moitié des conducteurs sur chacune des routes. Au finals le temps pour aller de A à C sera\(1+\frac{1}{2}=1,5\).

Ajoutons maintenant une super-route entre B et D. Extrêmement rapide et sans bouchons, on peut la parcourir presque instantanément. Dans cette nouvelle situation, les automobilistes peuvent si ils le souhaitent n'utiliser que des autoroutes et la super route. Comme c'est toujours le choix préférable, personne n'a intérêt à ne pas le faire. Au final tout le monde emprunte les autoroutes. Mais cela provocant des embouteillages, le temps total est alors\(2\) heures qui est pire que la situation sans la super route.

Se mettre en difficulté est parfois préférable.

Ici c'est un simple jeux à deux joueurs Valérie et Thomas et qui se joue en un seul tour. Valérie commence et choisit entre deux possibilités a ou b, puis c'est au tour de Thomas de choisir entre deux possibilités X ou Y. C'est fini. Chacun des joueurs gagnent le nombre de point selon le tableau suivant.

Chaque joueur vise le plus de gain possible. Valérie est donc capable de prédire le coup de Thomas. Si elle joue a, Thomas aura intéret à jouer X. Il gagnera alors 2 points alors et Valérie 4. Si maintenant Valérie joue b, alors elle doit s'attendre à ce que Thomas joue Y avec pour résultat 2 point pour Valérie et 5 point pour Thomas. Pour Valérie, la meilleur stratégie est donc de choisir a. Résultat final (4,2). Changeons maintenant la grille de la manière suivante.

Remarquez si les score de Valérie n'ont pas changés, quelque soit le résultat final Thomas gagne moins de point que la situation précédente. Reprenons maintenant le jeu: Si Valérie joue a, Thomas choisira Y ce qui n'intéresse pas du tout Valérie. Elle jouera donc\(b\) en sachant que Thomas jouera\(Y\) . Ici le résultat finale est (2,4). Mais alors Thomas gagne plus de points que précédemment. Conclusion, bien que sur toutes les combinaisons possible le résultat de Thomas est inférieur dans le deuxième jeu que dans le premier, Thomas gagne plus de points dans le deuxième jeu.