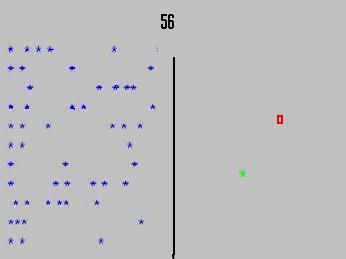
- The blue points: there where the radar discovers a boat.
- In red: the exact place of the boat.
- In green: the estimation by the algorithm, of the place of the boat.
- The figure in black represents the sold time.
 Version
française
Version
française
Work presented here is carried out in collaboration with Bruno Remillard (HEC Montreal) and Pierre Del Moral (LSP Toulouse). We present here two models of filtering allowing to find targets in a finite space. In this Web page, we present the studied models and simulations C++ and MATLAB.
1) First model, search for targets in disturbed images.
Problem : find boats in an image.
Boats, Markov chain, walk in a window of size T*T. A radar tries to find them. The redar observes every pixel of the window but regretably, he make errors of observations:
For the MATLAB and C++ simulations, we considered, one or two particles which follow an unpredictable walkimg to the closest neighbour whith probability to go up, go down, to go to the left and to go to the right-hand side. In the case fo tho particles one takes place in case they do not meet.
Here are the results of the simulations. We take place
in the case of an almost symmetric unpredictable walking. With p0=p1=0.9
orp0=p1=0.95.
The results are given in the form of small films. This
is an image in the case of one particle;
 |
|
For the search for only one boat (film MATLAB to be downloaded):
For the search for 2 boats, for reasons of computing time we are obliged to restrict itself with window of size 50*50:
- In a window 70*70 on 150 steps with p0=p1=0.9: filmt70n150.mat.gz(728 KB)
- In a window 200*200, on 500 steps and with p0=p1=0.9: filmt200n500.mat.gz(3.6 MB)
- In a window 200*200, on 200 steps and with p0=p1=0.9: filmt200n200.mat.gz
- In a window 200*200, on 200 steps and with p0=p1=0.95: filmt200n200p95.mat.gz
To show these films, it is necessary to download (right button of the mouse) one of the films, to unwind the file, to open MATLAB and to write the following commands (for the film filmt70n150.mat)
- Seek in a window 50*50, on 100 steps and with p0=p1=0.9: filmt50n100.mat.gz
- Seek in a window 50*50, on 100 steps and with p0=p1=0.95: filmt50n100p95.mat.gz(131 KB)
>>figureIf you don't have enough memory, you can see one image on 5 by writing:
>>% It is better to remove axes of the figure
>>load filmt70n150
>>movie(M)
>>movie(M,[1:5:150])Tables of the average errors:
Table 1 : The mean error in the case of one particle in a window of size 200*200.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 2 : The mean error in the case of two particles in a window of size 50*50.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Conclusion: In all the cases one can notice
that
the algorithm converges very quickly. If one leaves, with the first
iteration
of the uniform law on all the possible configurations, one notices that
one finds the two particles very quickly, at the 20-th iteration, the
estimate
is with one or two pixels of random walk. And as from the moment when
the
particles were found one does not leave them any more. Let us notice
moreover
than on the one hand one finds a particle more easily than two and on
the
other hand that the choice of the parameters p0 and p1 is significant
for
the speed of the algorithm.
Programm in C++ and article :